Skip to content

Navigation Menu

Sign in
Appearance settings

Search code, repositories, users, issues, pull requests...

Provide feedback

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly
Sign up
Appearance settings

[pull] master from youngyangyang04:master #76

New issue

Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.

By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.

Already on GitHub? Sign in to your account

Merged
pull merged 4 commits into AlgorithmAndLeetCode:master from youngyangyang04:master
Sep 3, 2022
Merged
Show file tree
Hide file tree
Changes from all commits
Commits
File filter

Filter by extension

Filter by extension
Conversations
Failed to load comments.
Loading
Jump to
Jump to file
Failed to load files.
Loading
Diff view
Diff view
14 changes: 14 additions & 0 deletions problems/0053.最大子序和(动态规划).md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -120,6 +120,20 @@ Java:
return res;
}
```
```Java
//因为dp[i]的递推公式只与前一个值有关,所以可以用一个变量代替dp数组,空间复杂度为O(1)
class Solution {
public int maxSubArray(int[] nums) {
int res = nums[0];
int pre = nums[0];
for(int i = 1; i < nums.length; i++) {
pre = Math.max(pre + nums[i], nums[i]);
res = Math.max(res, pre);
}
return res;
}
}
```

Python:
```python
Expand Down
2 changes: 2 additions & 0 deletions problems/0101.对称二叉树.md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -15,6 +15,8 @@

# 思路

《代码随想录》算法视频公开课:[同时操作两个二叉树 | LeetCode:101. 对称二叉树](https://www.bilibili.com/video/BV1ue4y1Y7Mf),相信结合视频在看本篇题解,更有助于大家对本题的理解。

**首先想清楚,判断对称二叉树要比较的是哪两个节点,要比较的可不是左右节点!**

对于二叉树是否对称,要比较的是根节点的左子树与右子树是不是相互翻转的,理解这一点就知道了**其实我们要比较的是两个树(这两个树是根节点的左右子树)**,所以在递归遍历的过程中,也是要同时遍历两棵树。
Expand Down
3 changes: 3 additions & 0 deletions problems/0102.二叉树的层序遍历.md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -6,6 +6,9 @@

# 二叉树层序遍历登场!

《代码随想录》算法视频公开课:[讲透二叉树的层序遍历 | 广度优先搜索 | LeetCode:102.二叉树的层序遍历](https://www.bilibili.com/video/BV1GY4y1u7b2),相信结合视频在看本篇题解,更有助于大家对本题的理解。


学会二叉树的层序遍历,可以一口气打完以下十题:

* 102.二叉树的层序遍历
Expand Down
3 changes: 3 additions & 0 deletions problems/0104.二叉树的最大深度.md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -31,6 +31,9 @@

本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。

* 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
* 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)

**而根节点的高度就是二叉树的最大深度**,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。

这一点其实是很多同学没有想清楚的,很多题解同样没有讲清楚。
Expand Down
42 changes: 41 additions & 1 deletion problems/0111.二叉树的最小深度.md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -31,7 +31,16 @@

直觉上好像和求最大深度差不多,其实还是差不少的。

遍历顺序上依然是后序遍历(因为要比较递归返回之后的结果),但在处理中间节点的逻辑上,最大深度很容易理解,最小深度可有一个误区,如图:
本题依然是前序遍历和后序遍历都可以,前序求的是深度,后序求的是高度。

* 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)
* 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数后者节点数(取决于高度从0开始还是从1开始)

那么使用后序遍历,其实求的是根节点到叶子节点的最小距离,就是求高度的过程,这不过这个最小距离 也同样是最小深度。

以下讲解中遍历顺序上依然采用后序遍历(因为要比较递归返回之后的结果,本文我也给出前序遍历的写法)。

本题还有一个误区,在处理节点的过程中,最大深度很容易理解,最小深度就不那么好理解,如图:

![111.二叉树的最小深度](https://img-blog.csdnimg.cn/20210203155800503.png)

Expand Down Expand Up @@ -150,6 +159,37 @@ public:

**精简之后的代码根本看不出是哪种遍历方式,所以依然还要强调一波:如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**

前序遍历的方式:

```CPP
class Solution {
private:
int result;
void getdepth(TreeNode* node, int depth) {
if (node->left == NULL && node->right == NULL) {
result = min(depth, result);
return;
}
// 中 只不过中没有处理的逻辑
if (node->left) { // 左
getdepth(node->left, depth + 1);
}
if (node->right) { // 右
getdepth(node->right, depth + 1);
}
return ;
}

public:
int minDepth(TreeNode* root) {
if (root == NULL) return 0;
result = INT_MAX;
getdepth(root, 1);
return result;
}
};
```

## 迭代法

相对于[104.二叉树的最大深度](https://programmercarl.com/0104.二叉树的最大深度.html),本题还可以使用层序遍历的方式来解决,思路是一样的。
Expand Down
5 changes: 3 additions & 2 deletions problems/0127.单词接龙.md
View file Open in desktop
Original file line number Diff line number Diff line change
Expand Up @@ -42,12 +42,11 @@
* 图中的线是如何连在一起的
* 起点和终点的最短路径长度


首先题目中并没有给出点与点之间的连线,而是要我们自己去连,条件是字符只能差一个,所以判断点与点之间的关系,要自己判断是不是差一个字符,如果差一个字符,那就是有链接。

然后就是求起点和终点的最短路径长度,**这里无向图求最短路,广搜最为合适,广搜只要搜到了终点,那么一定是最短的路径**。因为广搜就是以起点中心向四周扩散的搜索。

本题如果用深搜,会非常麻烦。
本题如果用深搜,会比较麻烦,要在到达终点的不同路径中选则一条最短路。 而广搜只要达到终点,一定是最短路。

另外需要有一个注意点:

Expand Down Expand Up @@ -96,6 +95,8 @@ public:
};
```

当然本题也可以用双向BFS,就是从头尾两端进行搜索,大家感兴趣,可以自己去实现,这里就不再做详细讲解了。

# 其他语言版本

## Java
Expand Down
80 changes: 80 additions & 0 deletions problems/0130.被围绕的区域.md
View file Open in desktop
Original file line number Diff line number Diff line change
@@ -0,0 +1,80 @@

# 130. 被围绕的区域

[题目链接](https://leetcode.cn/problems/surrounded-regions/)

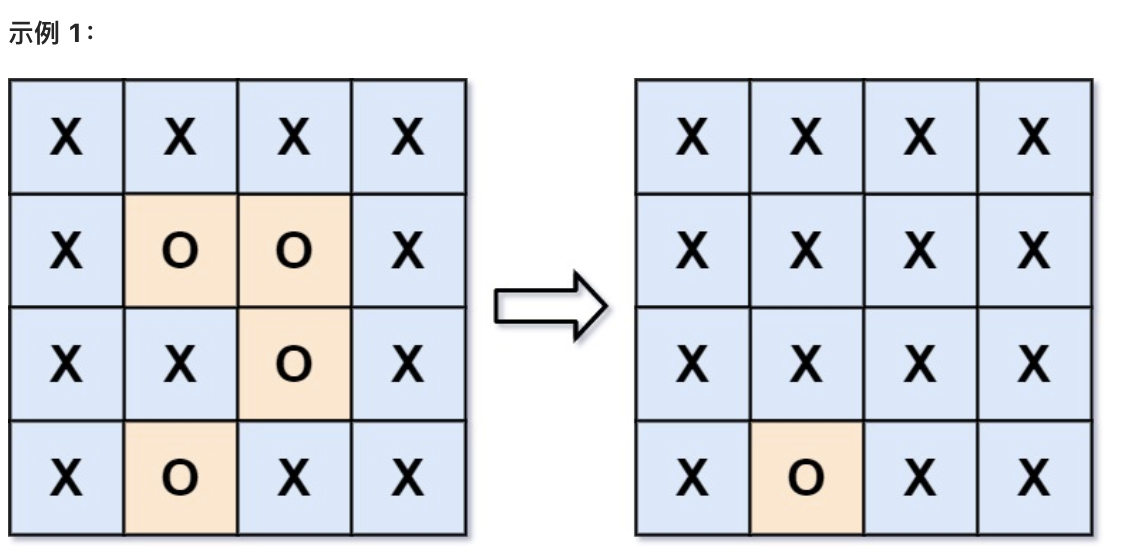
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。

![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220901104745.png)

* 输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
* 输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
* 解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是"相连"的。

## 思路

这道题目和1020. 飞地的数量正好反过来了,[1020. 飞地的数量](https://leetcode.cn/problems/number-of-enclaves/solution/by-carlsun-2-7lt9/)是求 地图中间的空格数,而本题是要把地图中间的'O'都改成'X'。

那么两题在思路上也是差不多的。

依然是从地图周边出发,将周边空格相邻的'O'都做上标记,然后在遍历一遍地图,遇到 'O' 且没做过标记的,那么都是地图中间的'O',全部改成'X'就行。

有的录友可能想,我在定义一个 visited 二维数组,单独标记周边的'O',然后遍历地图的时候同时对 数组board 和 数组visited 进行判断,是否'O'改成'X'。

这样做其实就有点麻烦了,不用额外定义空间了,标记周边的'O',可以直接改board的数值为其他特殊值。

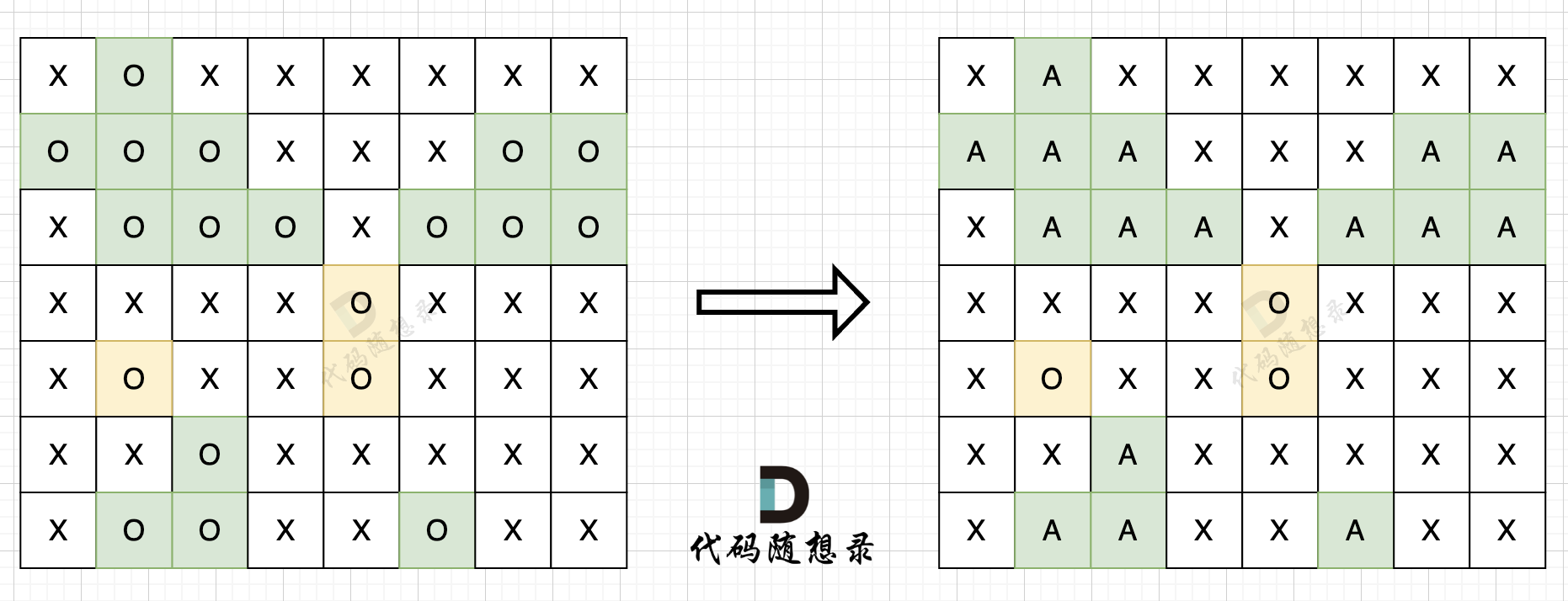
步骤一:深搜或者广搜将地图周边的'O'全部改成'A',如图所示:

![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902102337.png)

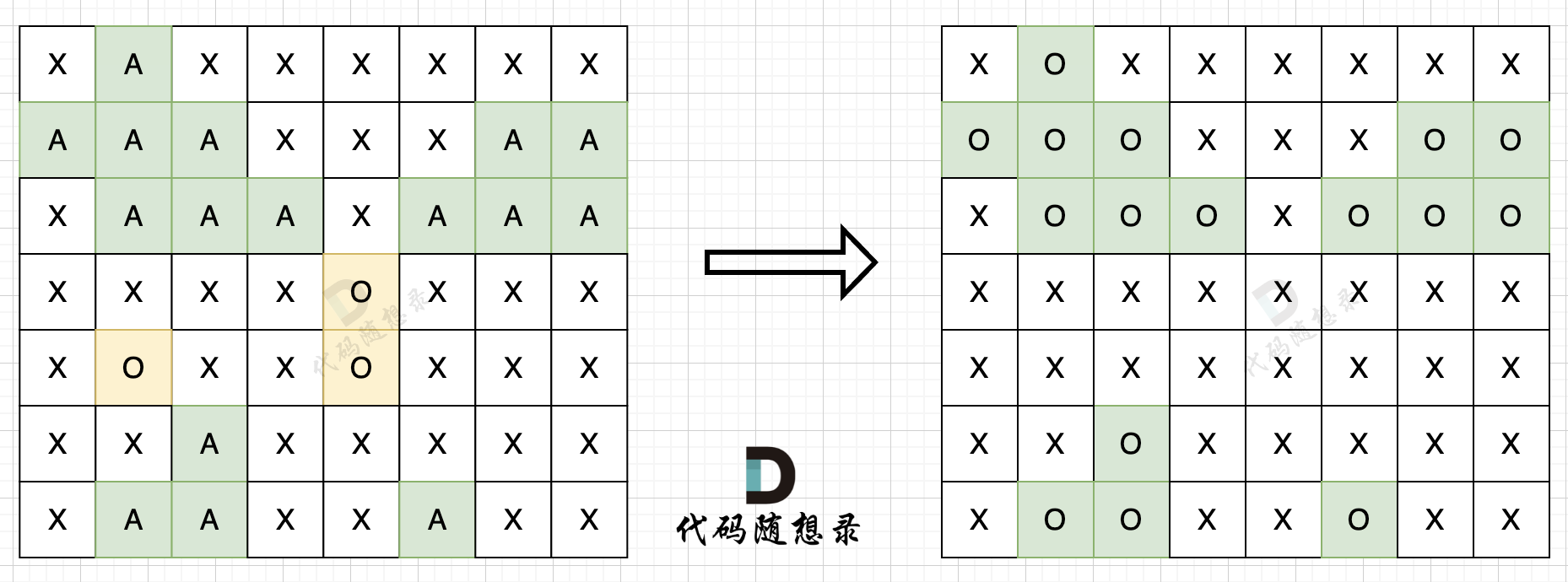
步骤二:在遍历地图,将'O'全部改成'X'(地图中间的'O'改成了'X'),将'A'改回'O'(保留的地图周边的'O'),如图所示:

![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220902102831.png)

整体C++代码如下,以下使用dfs实现,其实遍历方式dfs,bfs都是可以的。

```CPP
class Solution {
private:
int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
void dfs(vector<vector<char>>& board, int x, int y) {
board[x][y] = 'A';
for (int i = 0; i < 4; i++) { // 向四个方向遍历
int nextx = x + dir[i][0];
int nexty = y + dir[i][1];
// 超过边界
if (nextx < 0 || nextx >= board.size() || nexty < 0 || nexty >= board[0].size()) continue;
// 不符合条件,不继续遍历
if (board[nextx][nexty] == 'X' || board[nextx][nexty] == 'A') continue;
dfs (board, nextx, nexty);
}
return;
}

public:
void solve(vector<vector<char>>& board) {
int n = board.size(), m = board[0].size();
// 步骤一:
// 从左侧边,和右侧边 向中间遍历
for (int i = 0; i < n; i++) {
if (board[i][0] == 'O') dfs(board, i, 0);
if (board[i][m - 1] == 'O') dfs(board, i, m - 1);
}

// 从上边和下边 向中间遍历
for (int j = 0; j < m; j++) {
if (board[0][j] == 'O') dfs(board, 0, j);
if (board[n - 1][j] == 'O') dfs(board, n - 1, j);
}
// 步骤二:
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'O') board[i][j] = 'X';
if (board[i][j] == 'A') board[i][j] = 'O';
}
}
}
};
```

## 其他语言版本
146 changes: 146 additions & 0 deletions problems/0200.岛屿数量.广搜版.md
View file Open in desktop
Original file line number Diff line number Diff line change
@@ -0,0 +1,146 @@


# 200. 岛屿数量

[题目链接](https://leetcode.cn/problems/number-of-islands/)

给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。

岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外,你可以假设该网格的四条边均被水包围。

![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220726093256.png)

提示:

* m == grid.length
* n == grid[i].length
* 1 <= m, n <= 300
* grid[i][j] 的值为 '0' 或 '1'

## 思路

注意题目中每座岛屿只能由**水平方向和/或竖直方向上**相邻的陆地连接形成。

也就是说斜角度链接是不算了, 例如示例二,是三个岛屿,如图:

![图一](https://code-thinking-1253855093.file.myqcloud.com/pics/20220726094200.png)

这道题题目是 DFS,BFS,并查集,基础题目。

本题思路,是用遇到一个没有遍历过的节点陆地,计数器就加一,然后把该节点陆地所能遍历到的陆地都标记上。

在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。

那么如果把节点陆地所能遍历到的陆地都标记上呢,就可以使用 DFS,BFS或者并查集。

### 广度优先搜索

不少同学用广搜做这道题目的时候,超时了。 这里有一个广搜中很重要的细节:

根本原因是**只要 加入队列就代表 走过,就需要标记,而不是从队列拿出来的时候再去标记走过**。

很多同学可能感觉这有区别吗?

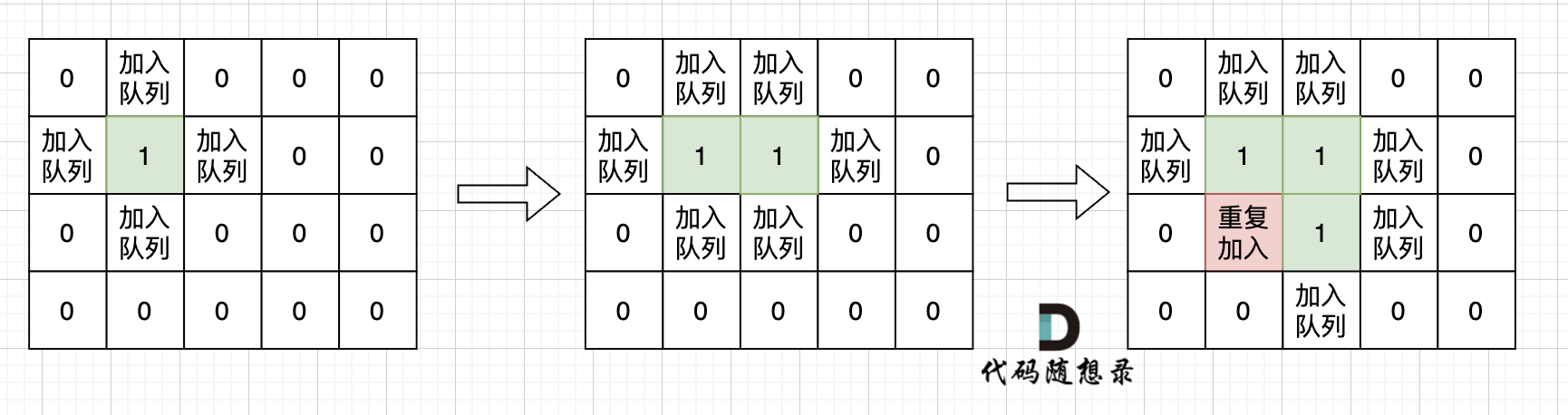
如果从队列拿出节点,再去标记这个节点走过,就会发生下图所示的结果,会导致很多节点重复加入队列。

![图二](https://code-thinking-1253855093.file.myqcloud.com/pics/20220727100846.png)

超时写法 (从队列中取出节点再标记)

```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
visited[curx][cury] = true; // 从队列中取出在标记走过
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
}
}
}

}
```

加入队列 就代表走过,立刻标记,正确写法:

```CPP
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列,立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}

}
```

以上两个版本其实,其实只有细微区别,就是 `visited[x][y] = true;` 放在的地方,着去取决于我们对 代码中队列的定义,队列中的节点就表示已经走过的节点。 **所以只要加入队列,理解标记该节点走过**。

本题完整广搜代码:

```CPP
class Solution {
private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
queue<pair<int, int>> que;
que.push({x, y});
visited[x][y] = true; // 只要加入队列,立刻标记
while(!que.empty()) {
pair<int ,int> cur = que.front(); que.pop();
int curx = cur.first;
int cury = cur.second;
for (int i = 0; i < 4; i++) {
int nextx = curx + dir[i][0];
int nexty = cury + dir[i][1];
if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue; // 越界了,直接跳过
if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
que.push({nextx, nexty});
visited[nextx][nexty] = true; // 只要加入队列立刻标记
}
}
}
}
public:
int numIslands(vector<vector<char>>& grid) {
int n = grid.size(), m = grid[0].size();
vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));

int result = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (!visited[i][j] && grid[i][j] == '1') {
result++; // 遇到没访问过的陆地,+1
bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
}
}
}
return result;
}
};

```
Loading

AltStyle によって変換されたページ (->オリジナル) /