@@ -1,129 +1,116 @@
## 1. 单调栈简介
> **单调栈(Monotone Stack)**:一种特殊的栈。在栈的「先进后出」规则基础上,要求「从 **栈顶** 到 **栈底** 的元素是单调递增(或者单调递减)」。其中满足从栈顶到栈底的元素是单调递增的栈,叫做「单调递增栈」。满足从栈顶到栈底的元素是单调递减的栈,叫做「单调递减栈」。
注意:这里定义的顺序是从「栈顶」到「栈底」。有的文章里是反过来的。本文全文以「栈顶」到「栈底」的顺序为基准来描述单调栈。
> **单调栈(Monotone Stack)**:在栈「先进后出」规则的基础上,要求从 **栈顶** 到 **栈底** 的元素单调递增或单调递减。
>
> - **单调递增栈**:从栈顶到栈底元素单调递增
> - **单调递减栈**:从栈顶到栈底元素单调递减
### 1.1 单调递增栈
> **单调递增栈**:只有比栈顶元素小的元素才能直接进栈,否则需要先将栈中比当前元素小的元素出栈,再将当前元素入栈 。
> **单调递增栈**:每次新元素进栈时,如果它比栈顶元素小,直接入栈;如果比栈顶元素大或相等,就把栈顶及以上所有小于等于它的元素依次弹出,直到栈顶比它大或栈空,再将新元素入栈 。
>
> 这样就保证了:栈中保留的都是比当前入栈元素大的值,并且从栈顶到栈底的元素值是单调递增的 。
> 这样可以保证:栈从栈顶到栈底的元素是递增的,且每个元素左侧第一个比它大的元素都能被快速找到 。
单调递增栈的入栈、出栈过程如下 :
单调递增栈的操作流程 :
- 假设当前进栈元素为 $x,ドル如果 $x$ 比栈顶元素小,则直接入栈 。
- 否则从栈顶开始遍历栈中元素,把小于 $x$ 或者等于 $x$ 的元素弹出栈,直到遇到一个大于 $x$ 的元素为止,然后再把 $x$ 压入栈中 。
- 当前元素 $x,ドル如果 $x$ < 栈顶元素,直接入栈 。
- 否则,不断弹出栈顶小于等于 $x$ 的元素,直到栈顶比 $x$ 大或栈空,然后将 $x$ 入栈 。
下面我们以数组 $[2, 7, 5, 4, 6, 3, 4, 2]$ 为例,模拟一下 「单调递增栈」的进栈、出栈过程。具体过程如下 :
下面以数组 $[2, 7, 5, 4, 6, 3, 4, 2]$ 为例,演示 「单调递增栈」的入栈与出栈过程 :
- 数组元素 :$[2, 7, 5, 4, 6, 3, 4, 2],ドル遍历顺序为从左到右 。
- 数组 :$[2, 7, 5, 4, 6, 3, 4, 2],ドル从左到右依次遍历 。
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作 用 |
| :----- : | :-------- : | ---------------------- | ------------------- | ------------------------------------- |
| 1 | 2 | 2 入栈 | [2] | 元素 2 的左侧无比 2 大的元素 |
| 2 | 7 | 2 出栈,7 入栈 | [7] | 元素 7 的左侧无比 7 大的元素 |
| 3 | 5 | 5 入栈 | [7, 5] | 元素 5 的左侧第一个比 5 大的元素为:7 |
| 4 | 4 | 4 入栈 | [7, 5, 4] | 元素 4 的左侧第一个比 4 大的元素为:5 |
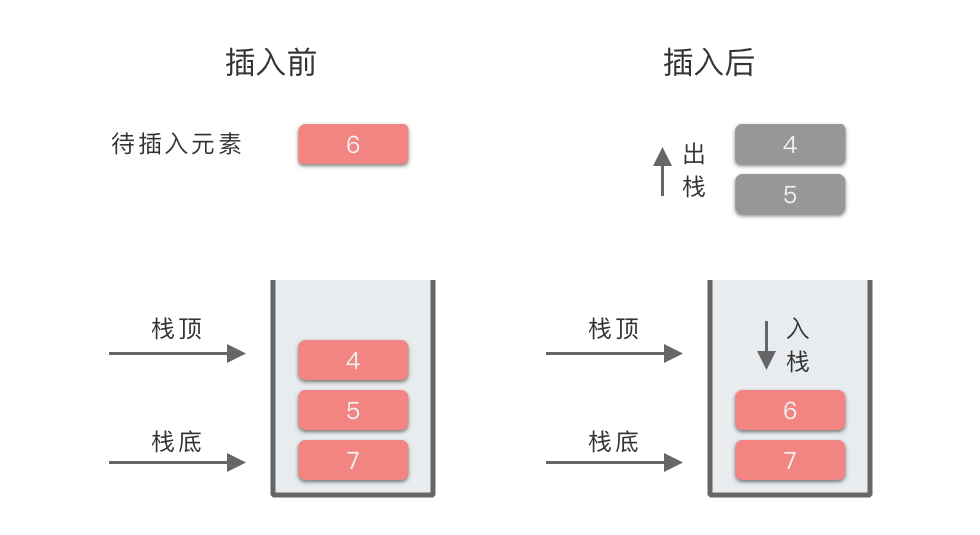
| 5 | 6 | 4 出栈,5 出栈,6 入栈 | [7, 6] | 元素 6 的左侧第一个比 6 大的元素为:7 |
| 6 | 3 | 3 入栈 | [7, 6, 3] | 元素 3 的左侧第一个比 3 大的元素为:6 |
| 7 | 4 | 3 出栈,4 入栈 | [7, 6, 4] | 元素 4 的左侧第一个比 4 大的元素为:6 |
| 8 | 2 | 2 入栈 | [7, 6, 4, 2] | 元素 2 的左侧第一个比 2 大的元素为:4 |
| 步骤 | 当前元素 | 操作 | 栈状态(左为栈底) | 说明 |
| :--: | :------: | ------------------------- | ------------------- | - ------------------------------------- |
| 1 | 2 | 2 入栈 | [2] | 2 左侧无更大元素 |
| 2 | 7 | 2 出栈,7 入栈 | [7] | 7 左侧无更大元素 |
| 3 | 5 | 5 入栈 | [7, 5] | 5 左侧第一个更大元素为 7 |
| 4 | 4 | 4 入栈 | [7, 5, 4] | 4 左侧第一个更大元素为 5 |
| 5 | 6 | 4 出栈,5 出栈,6 入栈 | [7, 6] | 6 左侧第一个更大元素为 7 |
| 6 | 3 | 3 入栈 | [7, 6, 3] | 3 左侧第一个更大元素为 6 |
| 7 | 4 | 3 出栈,4 入栈 | [7, 6, 4] | 4 左侧第一个更大元素为 6 |
| 8 | 2 | 2 入栈 | [7, 6, 4, 2] | 2 左侧第一个更大元素为 4 |
最终栈中元素为 $[7, 6, 4, 2]$。因为从栈顶(右端 )到栈底(左侧)元素的顺序为 2,ドル 4, 6, 7,ドル满足递增关系,所以这是一个单调递增栈 。
最终,栈中元素为 $[7, 6, 4, 2]$。从栈顶(右 )到栈底(左)为 2,ドル 4, 6, 7,ドル满足递增,符合单调递增栈的定义 。
我们以上述过程第 5 步为例,所对应的图示过程为 :
以第 5 步为例,图示如下 :
### 1.2 单调递减栈
> **单调递减栈**:只有比栈顶元素大的元素才能直接进栈,否则需要先将栈中比当前元素大的元素出栈,再将当前元素入栈 。
> **单调递减栈**:每次新元素进栈时,只有当它比栈顶元素大时才能直接入栈;如果小于或等于栈顶元素,则需要先将栈中所有大于等于当前元素的元素依次弹出,直到栈顶元素小于当前元素或栈为空,再将新元素入栈 。
>
> 这样就保证了:栈中保留的都是比当前入栈元素小的值,并且从栈顶到栈底的元素值是单调递减的 。
> 这样可以保证:栈中始终只保留比当前入栈元素小的值,并且从栈顶到栈底的元素是单调递减的 。
单调递减栈的入栈、出栈过程如下 :
单调递减栈的操作流程如下 :
- 假设当前进栈元素为 $x,ドル如果 $x$ 比栈顶元素大 ,则直接入栈。
- 否则从栈顶开始遍历栈中元素,把大于 $x$ 或者等于 $x$ 的元素弹出栈 ,直到遇到一个小于 $x$ 的元素为止,然后再把 $x$ 压入栈中 。
- 假设当前待入栈元素为 $x,ドル如果 $x$ > 栈顶元素 ,则直接入栈。
- 否则,从栈顶开始,依次弹出所有大于等于 $x$ 的元素 ,直到遇到一个小于 $x$ 的元素或栈为空,然后将 $x$ 入栈 。
下面我们以数组 $[4, 3, 2, 5, 7, 4, 6, 8]$ 为例,模拟一下 「单调递减栈」的进栈、出栈过程。具体过程如下 :
下面以数组 $[4, 3, 2, 5, 7, 4, 6, 8]$ 为例,演示 「单调递减栈」的入栈与出栈过程 :
- 数组元素 :$[4, 3, 2, 5, 7, 4, 6, 8],ドル遍历顺序为从左到右 。
- 数组 :$[4, 3, 2, 5, 7, 4, 6, 8],ドル从左到右依次遍历 。
| 第 i 步 | 待插入元素 | 操 作 | 结 果(左侧为栈底) | 作用 |
| :----- : | :-------- : | - --------------------- | ------------------- | ------------------------------------- |
| 1 | 4 | 4 入栈 | [4] | 元素 4 的左侧无比 4 小的元素 |
| 2 | 3 | 4 出栈,3 入栈 | [3] | 元素 3 的左侧无比 3 小的元素 |
| 3 | 2 | 3 出栈,2 入栈 | [2] | 元素 2 的左侧无比 2 小的元素 |
| 4 | 5 | 5 入栈 | [2, 5] | 元素 5 的左侧第一个比 5 小的元素是:2 |
| 5 | 7 | 7 入栈 | [2, 5, 7] | 元素 7 的左侧第一个比 7 小的元素是:5 |
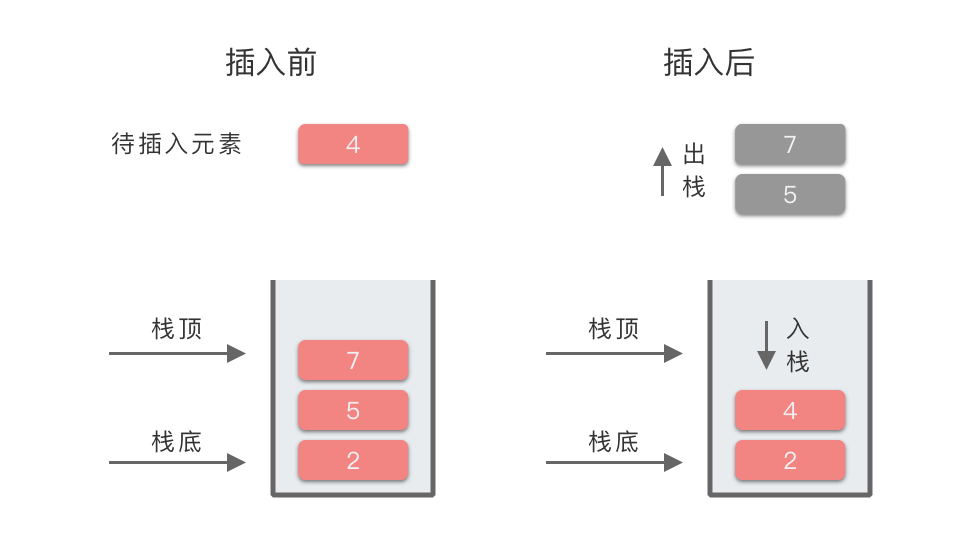
| 6 | 4 | 7 出栈,5 出栈,4 入栈| [2, 4] | 元素 4 的左侧第一个比 4 小的元素是:2 |
| 7 | 6 | 6 入栈 | [2, 4, 6] | 元素 6 的左侧第一个比 6 小的元素是:4 |
| 8 | 8 | 8 入栈 | [2, 4, 6, 8] | 元素 8 的左侧第一个比 8 小的元素是:6 |
| 步骤 | 当前元素 | 操作 | 栈状态(左为栈底) | 说明 |
| :--: | :------: | --------------------- | ------------------- | ------------------------------------- |
| 1 | 4 | 4 入栈 | [4] | 4 左侧无更小元素 |
| 2 | 3 | 4 出栈,3 入栈 | [3] | 3 左侧无更小元素 |
| 3 | 2 | 3 出栈,2 入栈 | [2] | 2 左侧无更小元素 |
| 4 | 5 | 5 入栈 | [2, 5] | 5 左侧第一个更小元素为 2 |
| 5 | 7 | 7 入栈 | [2, 5, 7] | 7 左侧第一个更小元素为 5 |
| 6 | 4 | 7 出栈,5 出栈,4 入栈| [2, 4] | 4 左侧第一个更小元素为 2 |
| 7 | 6 | 6 入栈 | [2, 4, 6] | 6 左侧第一个更小元素为 4 |
| 8 | 8 | 8 入栈 | [2, 4, 6, 8] | 8 左侧第一个更小元素为 6 |
最终栈中元素为 $[2, 4, 6, 8]$。因为从栈顶(右端 )到栈底(左侧)元素的顺序为 8,ドル 6, 4, 2,ドル满足递减关系,所以这是一个单调递减栈 。
最终,栈中元素为 $[2, 4, 6, 8]$。从栈顶(右 )到栈底(左)为 8,ドル 6, 4, 2,ドル满足递减,符合单调递减栈的定义 。
我们以上述过程第 6 步为例,所对应的图示过程为:
以第 6 步为例,图示如下:
## 2. 单调栈适用场景
单调栈可以在时间复杂度为 $O(n)$ 的情况下,求解出某个元素左边或者右边第一个比它大或者小的元素。
所以单调栈一般用于解决一下几种问题:
- 寻找左侧第一个比当前元素大的元素。
- 寻找左侧第一个比当前元素小的元素。
- 寻找右侧第一个比当前元素大的元素。
- 寻找右侧第一个比当前元素小的元素。
下面分别说一下这几种问题的求解方法。
### 2.1 寻找左侧第一个比当前元素大的元素
- 从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素左侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素大的元素。
单调栈常用于 $O(n)$ 时间复杂度内高效解决「最近更大/更小元素」类问题,主要包括以下四种典型场景:
- 查找左侧第一个比当前元素更大 / 更小的元素。
- 查找右侧第一个比当前元素更大 / 更小的元素。
### 2.2 寻找左侧第一个比当前元素小的元素
具体解法如下:
- 从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素左侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空,则说明左侧不存在比当前元素小的元素。
### 2.1 查找左侧第一个比当前元素大的元素
- 从左到右遍历数组,维护单调递增栈(栈顶到栈底递增):
- 当前元素入栈时,栈顶元素即为其左侧第一个更大元素;
- 若栈为空,则左侧不存在更大元素。
### 2.3 寻找右侧第一个比当前元素大的元素
### 2.2 查找左侧第一个比当前元素小的元素
- 从左到右遍历元素,构造单调递增栈(从栈顶到栈底递增 ):
- 一个元素右侧第一个比它大的元素就是将其「弹出单调递增栈」时即将插入的元素。
- 如果该元素没有被弹出栈,则说明右侧不存在比当前元素大的元素 。
- 从左到右遍历数组,维护单调递减栈(栈顶到栈底递减 ):
- 当前元素入栈时,栈顶元素即为其左侧第一个更小元素;
- 若栈为空,则左侧不存在更小元素 。
- 从右到左遍历元素,构造单调递增栈(从栈顶到栈底递增):
- 一个元素右侧第一个比它大的元素就是将其「插入单调递增栈」时的栈顶元素。
- 如果插入时的栈为空,则说明右侧不存在比当前元素大的元素。
### 2.3 查找右侧第一个比当前元素大的元素
- 从左到右遍历数组,维护单调递增栈:
- 当前元素将栈中比自己小的元素弹出,被弹出的元素的右侧第一个更大元素即为当前元素;
- 若某元素未被弹出,则右侧不存在更大元素。
- 或者,从右到左遍历,入栈时栈顶即为右侧第一个更大元素。
### 2.4 寻找右侧第一个比当前元素小的元素
### 2.4 查找右侧第一个比当前元素小的元素
- 从左到右遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素右侧第一个比它小的元素就是将其「弹出单调递减栈」时即将插入的元素。
- 如果该元素没有被弹出栈,则说明右侧不存在比当前元素小的元素。
- 从左到右遍历数组,维护单调递减栈:
- 当前元素将栈中比自己大的元素弹出,被弹出的元素的右侧第一个更小元素即为当前元素;
- 若某元素未被弹出,则右侧不存在更小元素。
- 或者,从右到左遍历,入栈时栈顶即为右侧第一个更小元素。
- 从右到左遍历元素,构造单调递减栈(从栈顶到栈底递减):
- 一个元素右侧第一个比它小的元素就是将其「插入单调递减栈」时的栈顶元素。
- 如果插入时的栈为空,则说明右侧不存在比当前元素小的元素。
上述四类问题可以归纳为以下通用规则:
上边的分类解法有点绕口,可以简单记为以下条规则:
- 无论哪种题型,都建议从左到右遍历元素。
- 查找 **「比当前元素大的元素」** 就用 **单调递增栈**,查找 **「比当前元素小的元素」** 就用 **单调递减栈**。
- 从 **「左侧」** 查找就看 **「插入栈」** 时的栈顶元素,从 **「右侧」** 查找就看 **「弹出栈」** 时即将插入的元素。
- 查「更大」用单调递增栈,查「更小」用单调递减栈;
- 查「左侧」看元素入栈时的栈顶;
- 查「右侧」看元素出栈时触发它的当前元素;
- 遍历方向通常为从左到右(部分场景可从右到左)。
## 3. 单调栈模板
Expand All
@@ -134,9 +121,12 @@
```python
def monotoneIncreasingStack(nums):
stack = []
for num in nums:
left
for i, num in enumerate(nums):
while stack and num >= stack[-1]:
stack.pop()
if stack:
stack.append(num)
```
Expand All
@@ -151,9 +141,11 @@ def monotoneDecreasingStack(nums):
stack.append(num)
```
## 4. 单调栈的应用
等号的去留(>= 或 >,<= 或 <)决定是否保留相等元素,按题意调整。
## 4. 单调栈的经典应用
### 4.1 下一个更大元素 I
### 4.1 经典例题: 下一个更大元素 I
#### 4.1.1 题目链接
Expand Down