@@ -1,107 +1,150 @@
## 1. 深度优先搜索简介
> **深度优先搜索算法(Depth First Search)**:英文缩写为 DFS,是一种用于搜索树或图结构的算法。深度优先搜索算法采用了回溯思想,从起始节点开始,沿着一条路径尽可能深入地访问节点,直到无法继续前进时为止,然后回溯到上一个未访问的节点,继续深入搜索,直到完成整个搜索过程。
## 1. 深度优先搜索简介
深度优先搜索算法中所谓的深度优先,就是说优先沿着一条路径走到底,直到无法继续深入时再回头。
> **深度优先搜索算法(Depth First Search)**:英文缩写为 DFS。是一种用于搜索树或图的算法。所谓深度优先,就是说每次都尝试向更深的节点走 。
在深度优先遍历的过程中,我们需要将当前遍历节点 $u$ 的相邻节点暂时存储起来,以便于在回退的时候可以继续访问它们。遍历到的节点顺序符合「后进先出」的特点,这正是「递归」和「堆栈」所遵循的规律,所以深度优先搜索可以通过「递归」或者「堆栈」来实现 。
深度优先搜索采用了回溯思想,该算法沿着树的深度遍历树的节点,会尽可能深的搜索树的分支。当节点 `v` 的所在边都己被探寻过,搜索将回溯到发现节点 `v` 的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
## 2. 深度优先搜索算法步骤
在深度优先遍历的过程中,我们需要将当前遍历节点 `v` 的相邻节点暂时存储起来,以便于在回退的时候可以继续访问它们。遍历到的节点顺序符合「后进先出」的特点,这正是「递归」和「堆栈」所遵循的规律,所以深度优先搜索可以通过「递归」或者「堆栈」来实现 。
接下来我们以一个无向图为例,介绍一下深度优先搜索的算法步骤 。
## 2. 深度优先搜索过程演示
1. 选择起始节点 $u,ドル并将其标记为已访问。
2. 检查当前节点是否为目标节点(看具体题目要求)。
3. 如果当前节点 $u$ 是目标节点,则直接返回结果。
4. 如果当前节点 $u$ 不是目标节点,则遍历当前节点 $u$ 的所有未访问邻接节点。
5. 对每个未访问的邻接节点 $v,ドル从节点 $v$ 出发继续进行深度优先搜索(递归)。
6. 如果节点 $u$ 没有未访问的相邻节点,回溯到上一个节点,继续搜索其他路径。
7. 重复 2ドル \sim 6$ 步骤,直到遍历完整个图或找到目标节点为止。
接下来我们以一个无向图为例,演示一下深度优先搜索的过程。
::: tabs#DFS
我们用邻接字典的方式存储无向图结构,对应结构如下:
@tab <1>
```python
# 定义无向图结构
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D"]
}
```
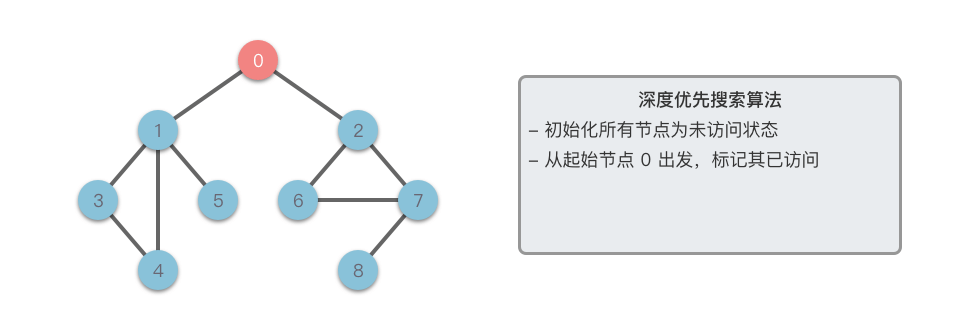
@tab <2>
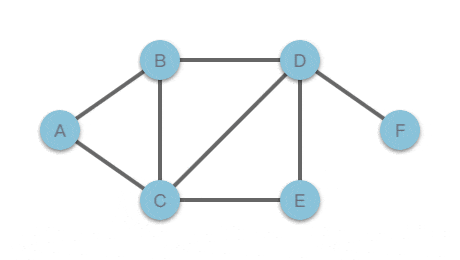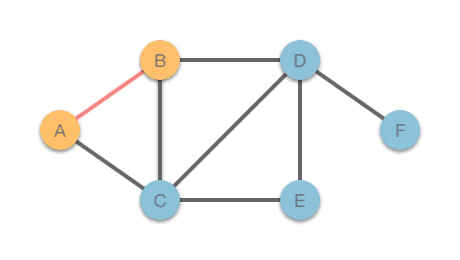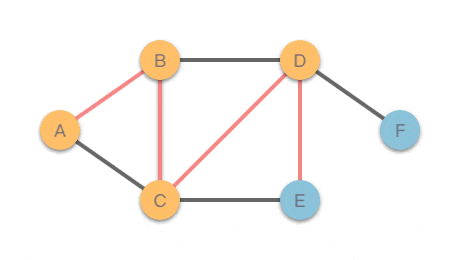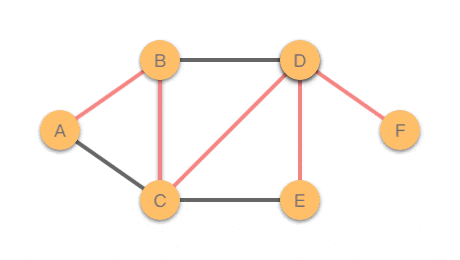
该无向图对应的邻接字典表示:无向图中有 `A`、`B`、`C`、`D`、`E`、`F` 共 `6` 个节点,其中与 `A` 节点相连的有 `B`、`C` 两个节点,与 `B` 节点相连的有 `A`、`C`、`D` 三个节点,等等。
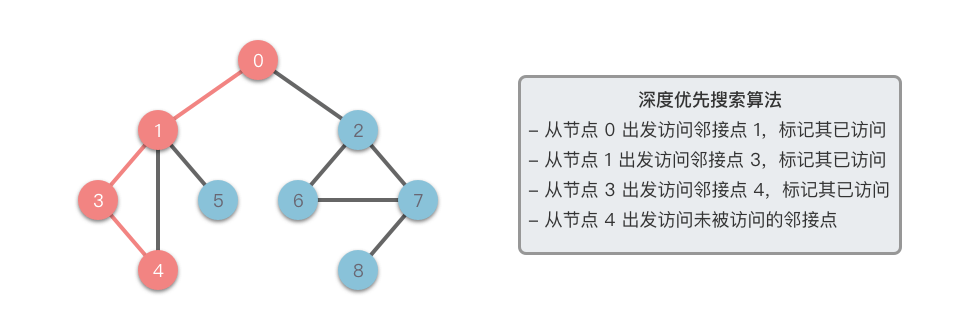
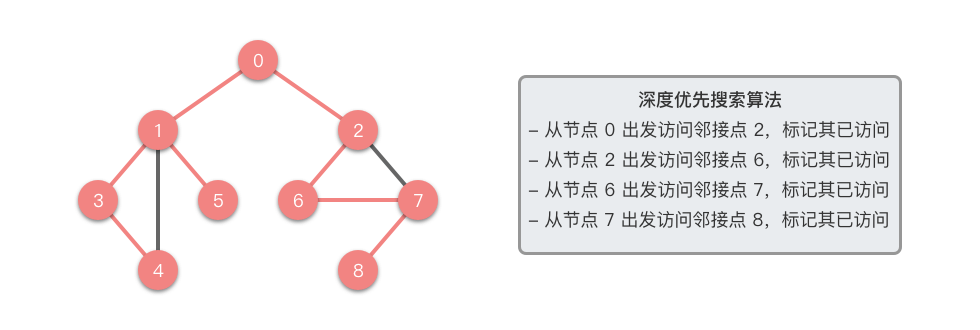
该无向图的结构如图左所示,其深度优先搜索的遍历路径如图右所示。
@tab <3>


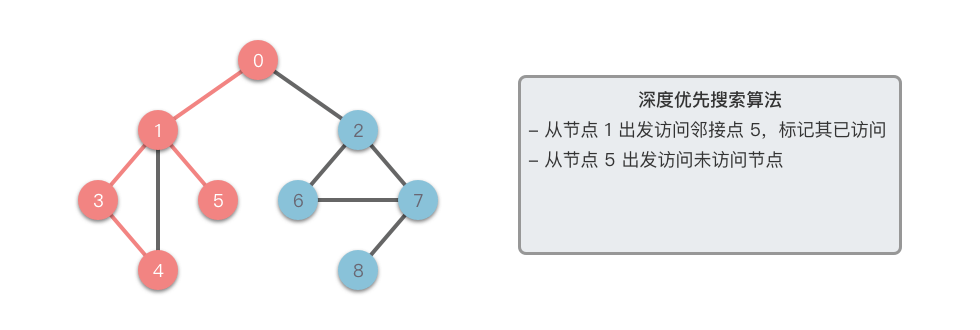
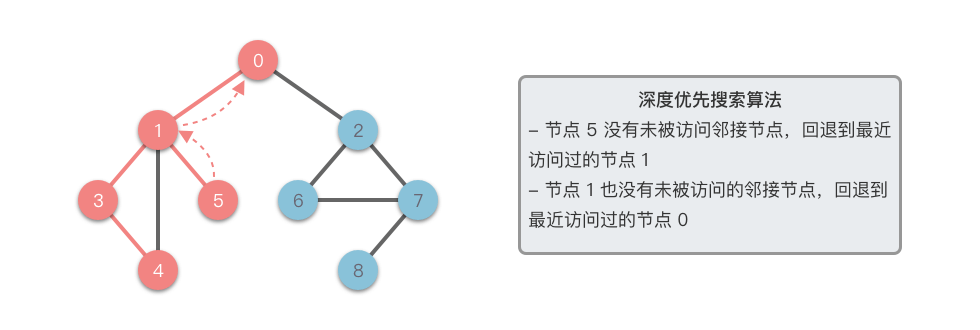
其深度优先搜索的遍历过程如下动态图所示。
@tab <4>
@tab <5>
@tab <6>
:::
## 3. 基于递归实现的深度优先搜索
### 3.1 基于递归实现的深度优先搜索实现步骤
### 3.1 基于递归实现的深度优先搜索算法步骤
深度优先搜索算法可以通过递归来实现,以下是基于递归实现的深度优先搜索算法步骤:
1. 定义 `graph` 为存储无向图的字典变量,`visited` 为标记访问节点的 set 集合变量。`start` 为当前遍历边的开始节点。`def dfs_recursive(graph, start, visited):` 为递归实现的深度优先搜索方法。
2. 将 `start` 标记为已访问,即将 `start` 节点放入 `visited` 中(`visited.add(start)`)。
3. 访问节点 `start`,并对节点进行相关操作(看具体题目要求)。
4. 遍历与节点 `start` 相连并构成边的节点 `end`。
1. 如果 `end` 没有被访问过,则从 `end` 节点调用递归实现的深度优先搜索方法,即 `dfs_recursive(graph, end, visited)`。
1. 定义 $graph$ 为存储无向图的嵌套数组变量,$visited$ 为标记访问节点的集合变量。$u$ 为当前遍历边的开始节点。定义 `def dfs_recursive(graph, u, visited):` 为递归实现的深度优先搜索方法。
2. 选择起始节点 $u,ドル并将其标记为已访问,即将节点 $u$ 放入 $visited$ 中(`visited.add(u)`)。
3. 检查当前节点 $u$ 是否为目标节点(看具体题目要求)。
4. 如果当前节点 $u$ 是目标节点,则直接返回结果。
5. 如果当前节点 $u$ 不是目标节点,则遍历当前节点 $u$ 的所有未访问邻接节点。
6. 对每个未访问的邻接节点 $v,ドル从节点 $v$ 出发继续进行深度优先搜索(递归),即调用 `dfs_recursive(graph, v, visited)`。
7. 如果节点 $u$ 没有未访问的相邻节点,则回溯到最近访问的节点,继续搜索其他路径。
8. 重复 3ドル \sim 7$ 步骤,直到遍历完整个图或找到目标节点为止。
### 3.2 基于递归实现的深度优先搜索实现代码
```python
def dfs_recursive(graph, start, visited):
# 标记节点
visited.add(start)
# 访问节点
print(start)
for end in graph[start]:
if end not in visited:
# 深度优先遍历节点
dfs_recursive(graph, end, visited)
class Solution:
def dfs_recursive(self, graph, u, visited):
print(u) # 访问节点
visited.add(u) # 节点 u 标记其已访问
for v in graph[u]:
if v not in visited: # 节点 v 未访问过
# 深度优先搜索遍历节点
self.dfs_recursive(graph, v, visited)
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D", "G"],
"G": []
}
# 基于递归实现的深度优先搜索
visited = set()
Solution().dfs_recursive(graph, "A", visited)
```
## 4. 基于堆栈实现的深度优先搜索
### 4.1 基于堆栈实现的深度优先搜索实现步骤
1. `start` 为开始节点。定义 `visited` 为标记访问节点的 set 集合变量。定义 `stack` 用于存放临时节点的栈结构。
2. 首先访问起始节点,并对节点进行相关操作(看具体题目要求)。
3. 然后将起始节点放入栈中,并标记访问。即 `visited = set(start)`,`stack = [start]`。
4. 如果栈不为空,取 `stack` 栈顶元素 `node_u`。
5. 遍历与节点 `node_u` 相连并构成边的节点 `node_v`。
- 如果 `node_v` 没有被访问过,则:
- 访问节点 `node_v`,并对节点进行相关操作(看具体题目要求)。
- 将 `node_v` 节点放入栈中,并标记访问,即 `stack.append(node_v)`,`visited.add(node_v)`。
- 跳出遍历 `node_v` 的循环。
- 继续遍历 `node_v`。
6. 如果 `node_u` 相邻的节点都访问结束了,从栈顶弹出 `node_u`,即 `stack.pop()`。
7. 重复步骤 4 ~ 6,直到 `stack` 为空。
### 4.1 基于堆栈实现的深度优先搜索算法步骤
深度优先搜索算法除了基于递归实现之外,还可以基于堆栈来实现。同时,为了防止多次遍历同一节点,在使用栈存放节点访问记录时,我们将「当前节点」以及「下一个将要访问的邻接节点下标」一同存入栈中,从而在出栈时,可以通过下标直接找到下一个邻接节点,而不用遍历所有邻接节点。
以下是基于堆栈实现的深度优先搜索的算法步骤:
1. 定义 $graph$ 为存储无向图的嵌套数组变量,$visited$ 为标记访问节点的集合变量。$start$ 为当前遍历边的开始节点。定义 $stack$ 用于存放节点访问记录的栈结构。
2. 选择起始节点 $u,ドル检查当前节点 $u$ 是否为目标节点(看具体题目要求)。
3. 如果当前节点 $u$ 是目标节点,则直接返回结果。
4. 如果当前节点 $u$ 不是目标节点,则将节点 $u$ 以及节点 $u$ 下一个将要访问的邻接节点下标 0ドル$ 放入栈中,并标记为已访问,即 `stack.append([u, 0])`,`visited.add(u)`。
5. 如果栈不为空,取出 $stack$ 栈顶元素节点 $u,ドル以及节点 $u$ 下一个将要访问的邻接节点下标 $i$。
6. 根据节点 $u$ 和下标 $i,ドル取出将要遍历的未访问过的邻接节点 $v$。
7. 将节点 $u$ 以及节点 u 的下一个邻接节点下标 $i + 1$ 放入栈中。
8. 访问节点 $v,ドル并对节点进行相关操作(看具体题目要求)。
9. 将节点 $v$ 以及节点 $v$ 下一个邻接节点下标 0ドル$ 放入栈中,并标记为已访问,即 `stack.append([v, 0])`,`visited.add(v)`。
10. 重复步骤 5ドル \sim 9,ドル直到 $stack$ 栈为空或找到目标节点为止。
### 4.2 基于堆栈实现的深度优先搜索实现代码
```python
def dfs_stack(graph, start) :
print(start) # 访问节点 start
visited = set(start ) # 使用 visited 标记访问过的节点,先标记 start
stack = [start] # 创建一个栈,并将 start 加入栈中
while stack:
node_u = stack[-1] # 取栈顶元素
class Solution :
def dfs_stack(self, graph, u):
print(u ) # 访问节点 u
visited, stack = set(), [] # 使用 visited 标记访问过的节点, 使用栈 stack 存放临时节点
stack.append([u, 0]) # 将节点 u,节点 u 的下一个邻接节点下标放入栈中,下次将遍历 graph[u][0]
visited.add(u) # 将起始节点 u 标记为已访问
i = 0
while i < len(graph[node_u]): # 遍历栈顶元素,遇到未访问节点,访问节点并跳出。
node_v = graph[node_u][i]
while stack:
u, i = stack.pop() # 取出节点 u,以及节点 u 下一个将要访问的邻接节点下标 i
if node_v not in visited: # node_v 未访问过
print(node_v) # 访问节点 node_v
stack.append(node_v) # 将 node_v 加入栈中
visited.add(node_v) # 标记为访问过 node_v
break
i += 1
if i < len(graph[u]):
v = graph[u][i] # 取出邻接节点 v
stack.append([u, i + 1]) # 下一次将遍历 graph[u][i + 1]
if v not in visited: # 节点 v 未访问过
print(v) # 访问节点 v
stack.append([v, 0]) # 下一次将遍历 graph[v][0]
visited.add(v) # 将节点 v 标记为已访问
if i == len(graph[node_u]): # node_u 相邻的节点都访问结束了,弹出 node_u
stack.pop()
graph = {
"A": ["B", "C"],
"B": ["A", "C", "D"],
"C": ["A", "B", "D", "E"],
"D": ["B", "C", "E", "F"],
"E": ["C", "D"],
"F": ["D", "G"],
"G": []
}
# 基于堆栈实现的深度优先搜索
Solution().dfs_stack(graph, "A")
```
## 5. 深度优先搜索应用
Expand All
@@ -125,10 +168,12 @@ def dfs_stack(graph, start):
- $m == grid.length$。
- $n == grid[i].length$。
- 1ドル \le m, n \le 300$。
- ` grid[i][j]` 的值为 `'0'` 或 `'1'`。
- $ grid[i][j]$ 的值为 `'0'` 或 `'1'`。
**示例**:
- 示例 1:
```python
输入:grid = [
["1","1","1","1","0"],
Expand All
@@ -137,8 +182,11 @@ def dfs_stack(graph, start):
["0","0","0","0","0"]
]
输出:1
```
- 示例 2:
```python
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
Expand All
@@ -156,10 +204,10 @@ def dfs_stack(graph, start):
##### 思路 1:深度优先搜索
1. 遍历 ` grid` 。
2. 对于每一个字符为 `'1'` 的元素,遍历其上下左右四个方向,并将该字符置为 `0 `,保证下次不会被重复遍历。
3. 如果超出边界,则返回 `0` 。
4. 对于 ` (i, j)` 位置的元素来说,递归遍历的位置就是 ` (i - 1, j)`、` (i, j - 1)`、` (i + 1, j)`、` (i, j + 1)` 四个方向。每次遍历到底,统计数记录一次。
1. 遍历 $ grid$ 。
2. 对于每一个字符为 `'1'` 的元素,遍历其上下左右四个方向,并将该字符置为 `'0' `,保证下次不会被重复遍历。
3. 如果超出边界,则返回 0ドル$ 。
4. 对于 $ (i, j)$ 位置的元素来说,递归遍历的位置就是 $ (i - 1, j)$、$ (i, j - 1)$、$ (i + 1, j)$、$ (i, j + 1)$ 四个方向。每次遍历到底,统计数记录一次。
5. 最终统计出深度优先搜索的次数就是我们要求的岛屿数量。
##### 思路 1:代码
Expand Down
Expand Up
@@ -200,16 +248,16 @@ class Solution:
#### 5.2.2 题目大意
**描述**:以每个节点的邻接列表形式(二维列表)给定一个无向连通图,其中 ` adjList[i]` 表示值为 ` i + 1` 的节点的邻接列表,` adjList[i][j]` 表示值为 ` i + 1` 的节点与值为 ` adjList[i][j]` 的节点有一条边。
**描述**:以每个节点的邻接列表形式(二维列表)给定一个无向连通图,其中 $ adjList[i]$ 表示值为 $ i + 1$ 的节点的邻接列表,$ adjList[i][j]$ 表示值为 $ i + 1$ 的节点与值为 $ adjList[i][j]$ 的节点有一条边。
**要求**:返回该图的深拷贝。
**说明**:
- 节点数不超过 ` 100` 。
- 节点数不超过 $ 100$ 。
- 每个节点值 $Node.val$ 都是唯一的,1ドル \le Node.val \le 100$。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 `p` 是节点 `q` 的邻居,那么节点 `q` 也必须是节点 `p` 的邻居。
- 由于图是无向的,如果节点 $p$ 是节点 $q$ 的邻居,那么节点 $q$ 也必须是节点 $p$ 的邻居。
- 图是连通图,你可以从给定节点访问到所有节点。
**示例**:
Expand Down
Expand Up
@@ -242,7 +290,7 @@ class Solution:
##### 思路 1:深度优先搜索
1. 使用哈希表 ` visitedDict` 来存储原图中被访问过的节点和克隆图中对应节点,键值对为原图被访问过的节点:克隆图中对应节点。
1. 使用哈希表 $ visitedDict$ 来存储原图中被访问过的节点和克隆图中对应节点,键值对为「 原图被访问过的节点:克隆图中对应节点」 。
2. 从给定节点开始,以深度优先搜索的方式遍历原图。
1. 如果当前节点被访问过,则返回隆图中对应节点。
2. 如果当前节点没有被访问过,则创建一个新的节点,并保存在哈希表中。
Expand Down