Expand Up
@@ -6,25 +6,25 @@
在学习之前,首先我们要弄清楚什么是算法?什么是数据结构?为什么要学习算法和数据结构?
简单来说,**算法(Algorithm) 就是解决问题的方法或者过程**。如果我们把问题看成是函数,那么算法就是将输入转换为输出的过程。**数据结构(Data Structure) 是数据的计算机表示和相应的一组操作**。**程序(Program) 则是算法和数据结构的具体实现**。
简单来说,**「算法」 就是解决问题的方法或者过程**。如果我们把问题看成是函数,那么算法就是将输入转换为输出的过程。**「 数据结构」 是数据的计算机表示和相应的一组操作**。**「程序」 则是算法和数据结构的具体实现**。
如果我们把「程序设计」比作是做菜的话,那么「数据结构」就是食材和调料,「算法」则是不同的烹饪方式,或者可以看作是菜谱。不同的食材和调料,不同的烹饪方式,有着不同的排列组合。同样的东西,由不同的人做出来,味道自然也是千差万别。
至于为什么要学习算法和数据结构?
还是拿做菜举例子。我们做菜,讲究的是「色香味」俱全 。**程序设计也是如此,对于待解决的问题,我们追求的是:选择更加合适的「数据结构」,使用花费时间更少、占用空间更小的「算法」。**
还是拿做菜举例子。我们做菜,讲究的是「色香味俱全」 。**程序设计也是如此,对于待解决的问题,我们追求的是:选择更加合适的「数据结构」,使用花费时间更少、占用空间更小的「算法」。**
我们学习算法和数据结构,是为了学会在编程中从时间复杂度、空间复杂度方面考虑解决方案,训练自己的逻辑思维,从而写出高质量的代码,以此提升自己的编程技能,获取更高的工作回报。
当然,这就像是做菜,掌握了食材和调料,学会了烹饪方式,并不意味着你就会做出一盘很好吃的炒菜。同样,掌握了算法和数据结构并不意味着你就会写程序。这需要不断的琢磨和思考,并持续学习,才能成为一名优秀的 ~~厨师~~(程序员)。
## 1. 数据结构
> 数据结构(Data Structure):带有结构特性的数据元素的集合。
> ** 数据结构(Data Structure)** :带有结构特性的数据元素的集合。
简单而言: **「数据结构」**指的是**数据的组织结构,用来组织、存储数据**。
简单而言, **「数据结构」**指的是: **数据的组织结构,用来组织、存储数据**。
展开来讲: 数据结构研究的是数据的逻辑结构、物理结构以及它们之间的相互关系,并对这种结构定义相应的运算,设计出相应的算法,并确保经过这些运算以后所得到的新结构仍保持原来的结构类型。
展开来讲, 数据结构研究的是数据的逻辑结构、物理结构以及它们之间的相互关系,并对这种结构定义相应的运算,设计出相应的算法,并确保经过这些运算以后所得到的新结构仍保持原来的结构类型。
数据结构的作用,就是为了提高计算机硬件的利用率。比如说:操作系统想要查找应用程序 「Microsoft Word」 在硬盘中的哪一个位置存储。如果对硬盘全部扫描一遍的话肯定效率很低,但如果使用「B+ 树」作为索引,就能很容易的搜索到 `Microsoft Word` 这个单词,然后很快的定位到 「Microsoft Word」这个应用程序的文件信息,从而从文件信息中找到对应的磁盘位置。
Expand All
@@ -36,55 +36,53 @@
### 1.1 数据的逻辑结构
> 逻辑结构(Logical Structure):数据元素之间的相互关系。
> ** 逻辑结构(Logical Structure)** :数据元素之间的相互关系。
根据元素之间具有的不同关系,通常我们可以将数据的逻辑结构分为以下四种:
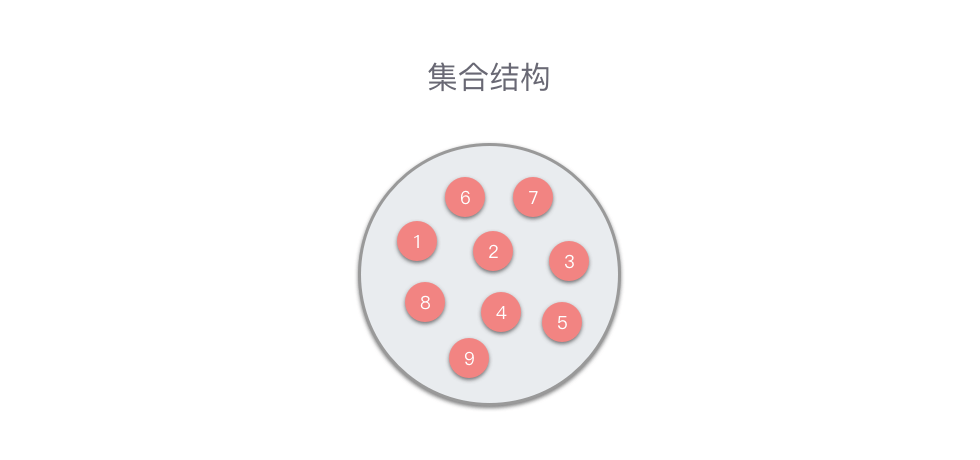
#### 1. 集合结构
- **集合结构**:数据元素同属于一个集合,除此之外无其他关系。
> **集合结构**:数据元素同属于一个集合,除此之外无其他关系。
集合结构中的数据元素是无序的,并且每个数据元素都是唯一的,集合中没有相同的数据元素。集合结构很像数学意义上的「集合」。
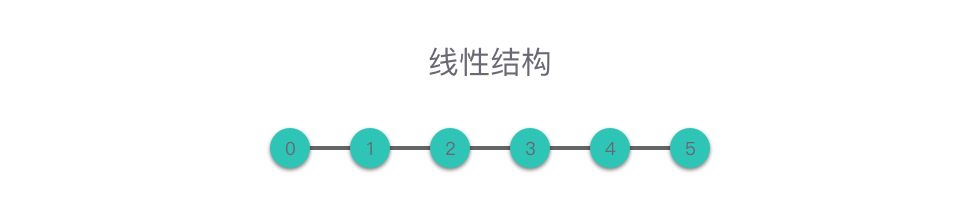
#### 2. 线性结构
- **线性结构**:数据元素之间是「一对一」关系。
> **线性结构**:数据元素之间是「一对一」关系。
线性结构中的数据元素(除了第一个和最后一个元素),左侧和右侧分别只有一个数据与其相邻。线性结构类型包括:数组、链表,以及由它们衍生出来的栈、队列、哈希表。
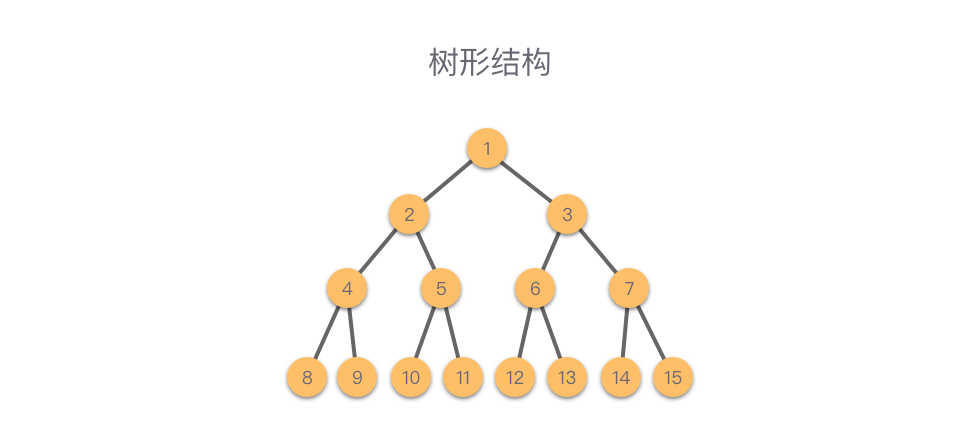
#### 3. 树形结构
- **树形结构**:数据元素之间是「一对多」的层次关系。
> **树形结构**:数据元素之间是「一对多」的层次关系。
最简单的树形结构是二叉树。这种结构可以简单的表示为:根, 左子树, 右子树。 左子树和右子树又有自己的子树。当然除了二叉树,树形结构类型还包括:多叉树、字典树等。
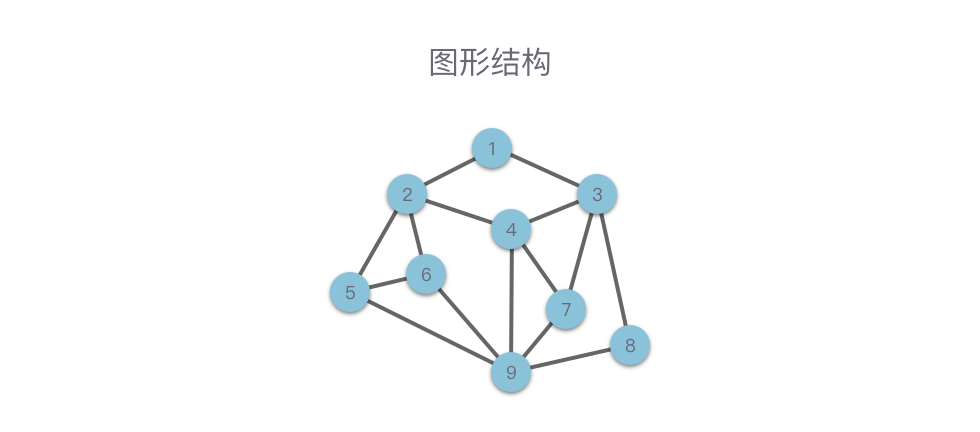
#### 4. 图形结构
- 图形结构:数据元素之间是「多对多」的关系。
> ** 图形结构** :数据元素之间是「多对多」的关系。
图形结构是一种比树形结构更复杂的非线性结构,用于表示物件与物件之间的关系。一张图由一些小圆点(称为 **顶点 ** 或 **结点 **)和连结这些圆点的直线或曲线(称为 **边 **)组成。
图形结构是一种比树形结构更复杂的非线性结构,用于表示物件与物件之间的关系。一张图由一些小圆点(称为 **「顶点」 ** 或 **「结点」 **)和连结这些圆点的直线或曲线(称为 **「边」 **)组成。
在图形结构中,任意两个结点之间都可能相关,即结点之间的邻接关系可以是任意的。图形结构类型包括:无向图、有向图、连通图等。
### 1.2 数据的物理结构
> 物理结构(Physical Structure):数据的逻辑结构在计算机中的存储方式。
> ** 物理结构(Physical Structure)** :数据的逻辑结构在计算机中的存储方式。
计算机内有多种存储结构,采用最多的是这两种结构:**顺序存储结构**、**链式存储结构**。
计算机内有多种存储结构,采用最多的是这两种结构:**「 顺序存储结构」 **、**「 链式存储结构」 **。
#### 1. 顺序存储结构
> 顺序存储结构(Sequential Storage Structure):将数据元素存放在一片地址连续的存储单元里,数据元素之间的逻辑关系通过数据元素的存储地址来直接反映。
> ** 顺序存储结构(Sequential Storage Structure)** :将数据元素存放在一片地址连续的存储单元里,数据元素之间的逻辑关系通过数据元素的存储地址来直接反映。

Expand All
@@ -94,7 +92,7 @@
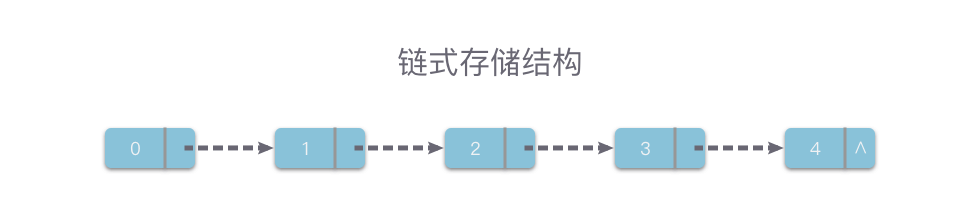
#### 2. 链式存储结构
> 链式存储结构(Linked Storage Structure):将数据元素存放在任意的存储单元里,存储单元可以连续,也可以不连续。
> ** 链式存储结构(Linked Storage Structure)** :将数据元素存放在任意的存储单元里,存储单元可以连续,也可以不连续。
Expand All
@@ -104,80 +102,80 @@
## 2. 算法
> 算法(Algorithm):解决特定问题求解步骤的准确而完整的描述,在计算机中表现为一系列指令的集合,算法代表着用系统的方法描述解决问题的策略机制。
> ** 算法(Algorithm)** :解决特定问题求解步骤的准确而完整的描述,在计算机中表现为一系列指令的集合,算法代表着用系统的方法描述解决问题的策略机制。
简单而言: **「算法」** 指的就是解决问题的方法。
简单而言, **「算法」** 指的就是解决问题的方法。
展开来讲: 算法是某一系列运算步骤,它表达解决某一类计算问题的一般方法,对这类方法的任何一个输入,它可以按步骤一步一步计算,最终产生一个输出。它不依赖于任何一种语言,可以用 **自然语言**、** 编程语言(Python、C、C++、Java 等)描述**,也可以用 **伪代码**、** 流程图** 来表示。
展开来讲, 算法是某一系列运算步骤,它表达解决某一类计算问题的一般方法,对这类方法的任何一个输入,它可以按步骤一步一步计算,最终产生一个输出。它不依赖于任何一种语言,可以用 **自然语言、 编程语言(Python、C、C++、Java 等)描述**,也可以用 **伪代码、 流程图** 来表示。
举几个例子来说明什么是算法 。
下面我们举几个例子来说明什么是算法 。
- 例一 :
- 示例 1 :
> 问题:从上海到北京,应该怎么去?
> **问题描述**:
>
> - 从上海到北京,应该怎么去?
>
> 解决方法:我们可以坐飞机,可以坐高铁,也可以坐长途汽车。不同的解决方案所带来的时间成本、金钱成本是不一样的。比如坐飞机用的时间最少,但费用最高,坐长途汽车费用低,但花费时间长。如果我们选择一个折中的方案,花费时间不算太长,价格也不算太贵,那我们可以选择坐高铁或火车。
> **解决方法**:
>
> 1. 选择坐飞机,坐飞机用的时间最少,但费用最高。
> 2. 选择坐长途汽车,坐长途汽车费用低,但花费时间长。
> 3. 选择坐高铁或火车,花费时间不算太长,价格也不算太贵。
- 例二 :
- 示例 2 :
> 问题:如何计算 1 + 2 + 3 + ... + 100 的值?
> **问题描述**:
>
> - 如何计算 1ドル + 2 + 3 + ... + 100$ 的值?
>
> 解决方法:我们可以选择用计算器从 1 开始,不断向右依次加上 2,再加上 3,再加上 ... 直到加到 100,得出结果为 5050。也可以选择直接根据高斯求和公式 `和 = (首项 + 末项) * 项数 / 2`,直接算出结果为 $ \frac{(1+100) * 100}{2} = 5050$。
> **解决方法**:
>
> 1. 用计算器从 1ドル$ 开始,不断向右依次加上 2ドル,ドル再加上 3ドル,ドル...,依次加到 100ドル,ドル得出结果为 5050ドル$。
> 2. 根据高斯求和公式:**和 = (首项 + 末项) * 项数 / 2**,直接算出结果为:$ \frac{(1+100) * 100}{2} = 5050$。
- 例三 :
- 示例 3 :
> 问题:如何对一个 n 个整数构成的数组进行升序排序?
> **问题描述**:
>
> - 如何对一个 $n$ 个整数构成的数组进行升序排序?
>
> 解决方法:我们可以选择冒泡排序对这 n 个整数进行排序,也可以选择插入排序、归并排序、快速排序等等。
> **解决方法**:
>
> 1. 使用冒泡排序对 $n$ 个整数构成的数组进行升序排序。
> 2. 选择插入排序、归并排序、快速排序等等其他排序算法对 $n$ 个整数构成的数组进行升序排序。
以上三例都可以看做是算法。从上海去北京的方法可以看做是算法 ,对 1~ 100 的数进行求和的计算方法也可以看做是算法。对数组进行排序的方法也可以看做是算法。并且从这三个例子可以看出对于一个特定的问题 ,往往有着不同的算法。
以上 3ドル$ 个示例中的解决方法都可以看做是算法。从上海去北京的解决方法可以看做是算法 ,对 1ドル \sim 100$ 的数进行求和的计算方法也可以看做是算法。对数组进行排序的方法也可以看做是算法。并且从这 3ドル$ 个示例中可以看出对于一个特定的问题 ,往往有着不同的算法。
### 2.1 算法的基本特性
算法其实就是一系列的运算步骤,这些运算步骤可以解决特定的问题。除此之外,**算法** 应必须具备以下特性。
##### 1. 输入
对于待解决的问题,都要以某种方式交给对应的算法。在算法开始之前最初赋给算法的参数称为输入。比如例一中的输入就是出发地和目的地的参数(北京,上海),例三中的输入就是 n 个整数构成的数组。
一个算法可以有多个输入,也可以没有输入。比如例二是对固定问题的求解,就可以看做没有输入。
##### 2. 输出
算法是为了解决问题存在的,最终总需要返回一个结果。所以至少需要一个或多个参数作为算法的输出。比如例一中的输出就是最终选择的交通方式,例二中的输出就是和的结果。例三中的输出就是排好序的数组。
##### 3. 有穷性
算法必须在有限的步骤内结束,并且应该在一个可接受的时间内完成。比如例一,如果我们选择五一从上海到北京去旅游,结果五一纠结了三天也没决定好怎么去北京,那么这个旅游计划也就泡汤了,这个算法自然也是不合理的。
##### 4. 确定性
组成算法的每一条指令必须有着清晰明确的含义,不能令读者在理解时产生二义性或者多义性。就是说,算法的每一个步骤都必须准确定义而无歧义。
##### 5. 可行性
算法其实就是一系列的运算步骤,这些运算步骤可以解决特定的问题。除此之外,**算法** 应必须具备以下特性:
算法的每一步操作必须具有可执行性,在当前环境条件下可以通过有限次运算实现。也就是说,每一步都能通过执行有限次数完成,并且可以转换为程序在计算机上运行并得到正确的结果。
1. **输入**:对于待解决的问题,都要以某种方式交给对应的算法。在算法开始之前最初赋给算法的参数称为输入。比如示例 1ドル$ 中的输入就是出发地和目的地的参数(北京,上海),示例 3ドル$ 中的输入就是 $n$ 个整数构成的数组。一个算法可以有多个输入,也可以没有输入。比如示例 2ドル$ 是对固定问题的求解,就可以看做没有输入。
2. **输出**:算法是为了解决问题存在的,最终总需要返回一个结果。所以至少需要一个或多个参数作为算法的输出。比如示例 1ドル$ 中的输出就是最终选择的交通方式,示例 2ドル$ 中的输出就是和的结果。示例 3ドル$ 中的输出就是排好序的数组。
3. **有穷性**:算法必须在有限的步骤内结束,并且应该在一个可接受的时间内完成。比如示例 1ドル,ドル如果我们选择五一从上海到北京去旅游,结果五一纠结了三天也没决定好怎么去北京,那么这个旅游计划也就泡汤了,这个算法自然也是不合理的。
4. **确定性**:组成算法的每一条指令必须有着清晰明确的含义,不能令读者在理解时产生二义性或者多义性。就是说,算法的每一个步骤都必须准确定义而无歧义。
5. **可行性**:算法的每一步操作必须具有可执行性,在当前环境条件下可以通过有限次运算实现。也就是说,每一步都能通过执行有限次数完成,并且可以转换为程序在计算机上运行并得到正确的结果。
### 2.2 算法追求的目标
研究算法的作用,就是为了使解决问题的方法变得更加高效。对于给定的问题,我们往往会有多种算法来解决。而不同算法的 **成本** 也是不同的。总体而言,一个优秀的算法至少应该追求以下两个目标:
1. 所需运行时间更少(时间复杂度更低);
2. 占用内存空间更小(空间复杂度更低)。
1. ** 所需运行时间更少(时间复杂度更低)** ;
2. ** 占用内存空间更小(空间复杂度更低)** 。
假设计算机执行一条命令的时间为 1 纳秒(并不科学),第一种算法需要执行 100 纳秒,第二种算法则需要执行 3 纳秒。如果不考虑占用内存空间的话,很明显第二种算法比第一种算法要好很多。
假设计算机执行一条命令的时间为 1ドル$ 纳秒(并不科学),第一种算法需要执行 $ 100$ 纳秒,第二种算法则需要执行 3ドル$ 纳秒。如果不考虑占用内存空间的话,很明显第二种算法比第一种算法要好很多。
假设计算机一个内存单元的大小为一个字节,第一种算法需要占用 3 个字节大小的内存空间,第二种算法则需要占用 100 个字节大小的内存空间,如果不考虑运行时间的话,很明显第一种算法比第二种算法要好很多。
假设计算机一个内存单元的大小为一个字节,第一种算法需要占用 3ドル$ 个字节大小的内存空间,第二种算法则需要占用 $ 100$ 个字节大小的内存空间,如果不考虑运行时间的话,很明显第一种算法比第二种算法要好很多。
现实中算法,往往是需要同时从运行时间、占用空间两个方面考虑问题。当然,运行时间越少,占用空间越小的算法肯定是越好的,但总是会有各种各样的因素导致了运行时间和占用空间不可兼顾。比如,在程序运行时间过高时,我们可以考虑在空间上做文章,牺牲一定量的空间,来换取更短的运行时间。或者在程序对运行时间要求不是很高,而设备内存又有限的情况下,选择占用空间更小,但需要牺牲一定量的时间的算法。
当然,除了对运行时间和占用内存空间的追求外,一个好的算法还应该追求以下目标:
1. 正确性:正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
2. 可读性:可读性指的是算法遵循标识符命名规则,简洁易懂,注释语句恰当,方便自己和他人阅读,便于后期修改和调试。
3. 健壮性:健壮性指的是算法对非法数据以及操作有较好的反应和处理。
1. ** 正确性** :正确性是指算法能够满足具体问题的需求,程序运行正常,无语法错误,能够通过典型的软件测试,达到预期的需求。
2. ** 可读性** :可读性指的是算法遵循标识符命名规则,简洁易懂,注释语句恰当,方便自己和他人阅读,便于后期修改和调试。
3. ** 健壮性** :健壮性指的是算法对非法数据以及操作有较好的反应和处理。
这 3 个目标是算法的基本标准,是所有算法所必须满足的。一般我们对好的算法的评判标准就是上边提到的 **所需运行时间更少(时间复杂度更低)**、**占用内存空间更小(空间复杂度更低)**。
这 3ドル$ 个目标是算法的基本标准,是所有算法所必须满足的。一般我们对好的算法的评判标准就是上边提到的 **所需运行时间更少(时间复杂度更低)**、**占用内存空间更小(空间复杂度更低)**。
## 3. 总结
Expand Down