curLevelNodes) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2271円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2271円.md"
index 64fd4e7497..e3133eb6cb 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2271円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2271円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -150,7 +150,7 @@ TreeNode invertTree(TreeNode root) {
这是力扣第 116 题「填充每个二叉树节点的右侧指针」,看下题目:
-
+
函数签名如下:
@@ -160,7 +160,7 @@ Node connect(Node root);
题目的意思就是把二叉树的每一层节点都用 `next` 指针连接起来:
-
+
而且题目说了,输入是一棵「完美二叉树」,形象地说整棵二叉树是一个正三角形,除了最右侧的节点 `next` 指针会指向 `null`,其他节点的右侧一定有相邻的节点。
@@ -190,7 +190,7 @@ void traverse(Node root) {
但是,这段代码其实有很大问题,因为它只能把相同父节点的两个节点穿起来,再看看这张图:
-
+
节点 5 和节点 6 不属于同一个父节点,那么按照这段代码的逻辑,它俩就没办法被穿起来,这是不符合题意的,但是问题出在哪里?
@@ -198,7 +198,7 @@ void traverse(Node root) {
所以我们可以在二叉树的基础上进行抽象,你把图中的每一个方框看做一个节点:
-
+
**这样,一棵二叉树被抽象成了一棵三叉树,三叉树上的每个节点就是原先二叉树的两个相邻节点**。
@@ -240,7 +240,7 @@ void traverse(Node node1, Node node2) {
这是力扣第 114 题「将二叉树展开为链表」,看下题目:
-
+
函数签名如下:
@@ -292,7 +292,7 @@ void flatten(TreeNode root);
2、将 `x` 的右子树接到左子树下方,然后将整个左子树作为右子树。
-
+
这样,以 `x` 为根的整棵二叉树就被拉平了,恰好完成了 `flatten(x)` 的定义。
@@ -391,7 +391,7 @@ void flatten(TreeNode root) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2272円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2272円.md"
index 1d7ea84955..b6afc26fa4 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2272円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/344円272円214円345円217円211円346円240円221円347円263円273円345円210円2272円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -49,7 +49,7 @@ PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了
先来道简单的,这是力扣第 654 题「最大二叉树」,题目如下:
-
+
函数签名如下:
@@ -139,7 +139,7 @@ TreeNode build(int[] nums, int lo, int hi) {
力扣第 105 题「从前序和中序遍历序列构造二叉树」就是这道经典题目,面试笔试中常考:
-
+
函数签名如下:
@@ -171,7 +171,7 @@ void traverse(TreeNode root) {
前文 [二叉树就那几个框架](https://labuladong.github.io/article/fname.html?fname=nestInteger) 写过,这样的遍历顺序差异,导致了 `preorder` 和 `inorder` 数组中的元素分布有如下特点:
-
+
找到根节点是很简单的,前序遍历的第一个值 `preorder[0]` 就是根节点的值。
@@ -219,7 +219,7 @@ TreeNode build(int[] preorder, int preStart, int preEnd,
对于代码中的 `rootVal` 和 `index` 变量,就是下图这种情况:
-
+
另外,也有读者注意到,通过 for 循环遍历的方式去确定 `index` 效率不算高,可以进一步优化。
@@ -259,7 +259,7 @@ root.right = build(preorder, ?, ?,
对于左右子树对应的 `inorder` 数组的起始索引和终止索引比较容易确定:
-
+
```java
root.left = build(preorder, ?, ?,
@@ -273,7 +273,7 @@ root.right = build(preorder, ?, ?,
这个可以通过左子树的节点数推导出来,假设左子树的节点数为 `leftSize`,那么 `preorder` 数组上的索引情况是这样的:
-
+
看着这个图就可以把 `preorder` 对应的索引写进去了:
@@ -322,7 +322,7 @@ TreeNode build(int[] preorder, int preStart, int preEnd,
类似上一题,这次我们利用**后序**和**中序**遍历的结果数组来还原二叉树,这是力扣第 106 题「从后序和中序遍历序列构造二叉树」:
-
+
函数签名如下:
@@ -350,7 +350,7 @@ void traverse(TreeNode root) {
这样的遍历顺序差异,导致了 `postorder` 和 `inorder` 数组中的元素分布有如下特点:
-
+
这道题和上一题的关键区别是,后序遍历和前序遍历相反,根节点对应的值为 `postorder` 的最后一个元素。
@@ -394,7 +394,7 @@ TreeNode build(int[] inorder, int inStart, int inEnd,
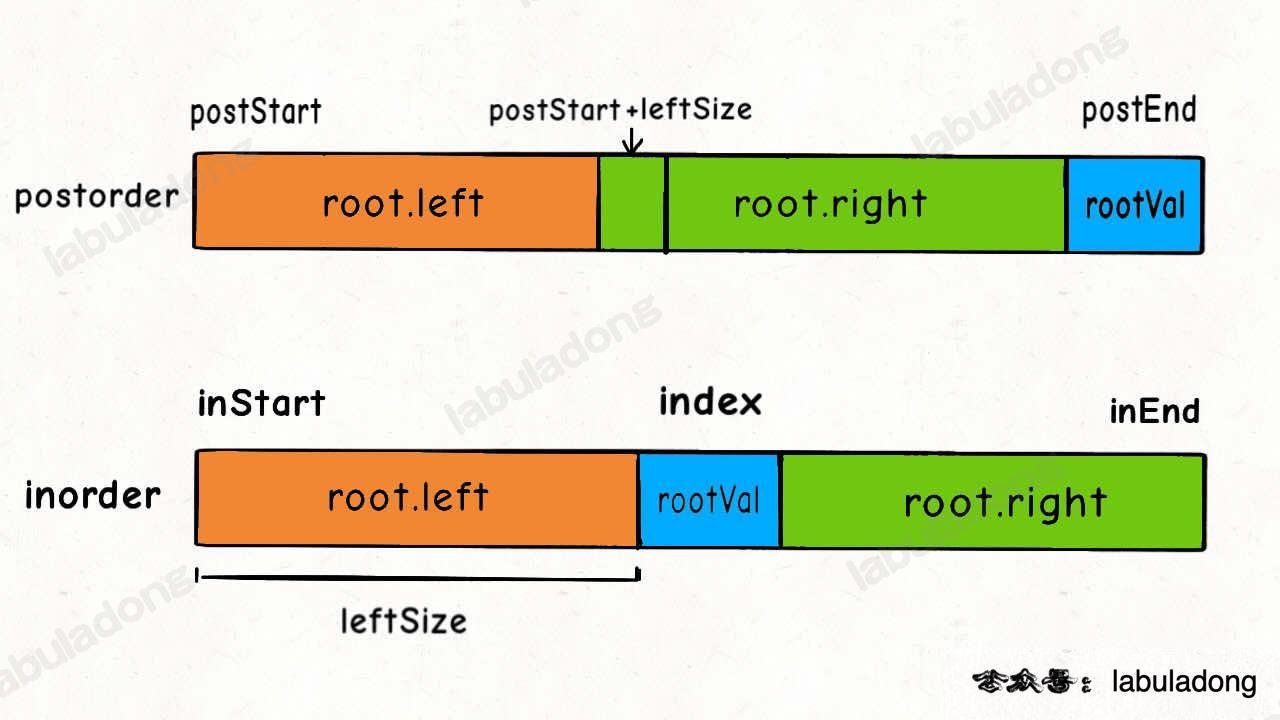
现在 `postoder` 和 `inorder` 对应的状态如下:
-
+
我们可以按照上图将问号处的索引正确填入:
@@ -466,7 +466,7 @@ preorder = [1,2,3], postorder = [3,2,1]
下面这两棵树都是符合条件的,但显然它们的结构不同:
-
+
不过话说回来,用后序遍历和前序遍历结果还原二叉树,解法逻辑上和前两道题差别不大,也是通过控制左右子树的索引来构建:
@@ -476,7 +476,7 @@ preorder = [1,2,3], postorder = [3,2,1]
**3、在后序遍历结果中寻找左子树根节点的值,从而确定了左子树的索引边界,进而确定右子树的索引边界,递归构造左右子树即可**。
-
+
详情见代码。
@@ -586,4 +586,4 @@ int leftRootVal = preorder[preStart + 1];
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円346円240円210円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円346円240円210円.md"
index eb41a6f739..2fc364c059 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円346円240円210円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円346円240円210円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -41,7 +41,7 @@ int[] nextGreaterElement(int[] nums);
这个问题可以这样抽象思考:把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素「2」的下一个更大元素呢?很简单,如果能够看到元素「2」,那么他后面可见的第一个人就是「2」的下一个更大元素,因为比「2」小的元素身高不够,都被「2」挡住了,第一个露出来的就是答案。
-
+
这个情景很好理解吧?带着这个抽象的情景,先来看下代码。
@@ -76,7 +76,7 @@ int[] nextGreaterElement(int[] nums) {
单调栈的使用技巧差不多了,首先来一个简单的变形,力扣第 496 题「下一个更大元素 I」:
-
+
这道题给你输入两个数组 `nums1` 和 `nums2`,让你求 `nums1` 中的元素在 `nums2` 中的下一个更大元素,函数签名如下:
@@ -167,7 +167,7 @@ while (true) {
**对于这种需求,常用套路就是将数组长度翻倍**:
-
+
这样,元素 3 就可以找到元素 4 作为下一个更大元素了,而且其他的元素都可以被正确地计算。
@@ -238,7 +238,7 @@ int[] nextGreaterElements(int[] nums) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円351円230円237円345円210円227円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円351円230円237円345円210円227円.md"
index aca673f636..84bcfb797f 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円351円230円237円345円210円227円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円215円225円350円260円203円351円230円237円345円210円227円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -55,7 +55,7 @@ int[] maxSlidingWindow(int[] nums, int k);
比如说力扣给出的一个示例:
-
+
接下来,我们就借助单调队列结构,用 `O(1)` 时间算出每个滑动窗口中的最大值,使得整个算法在线性时间完成。
@@ -115,7 +115,7 @@ int[] maxSlidingWindow(int[] nums, int k) {
}
```
-
+
这个思路很简单,能理解吧?下面我们开始重头戏,单调队列的实现。
@@ -143,7 +143,7 @@ public void push(int n) {
你可以想象,加入数字的大小代表人的体重,把前面体重不足的都压扁了,直到遇到更大的量级才停住。
-
+
如果每个元素被加入时都这样操作,最终单调队列中的元素大小就会保持一个**单调递减**的顺序,因此我们的 `max` 方法可以可以这样写:
@@ -166,7 +166,7 @@ public void pop(int n) {
之所以要判断 `data.getFirst() == n`,是因为我们想删除的队头元素 `n` 可能已经被「压扁」了,可能已经不存在了,所以这时候就不用删除了:
-
+
至此,单调队列设计完毕,看下完整的解题代码:
@@ -300,7 +300,7 @@ class MonotonicQueue
> {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円233円276円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円233円276円.md"
index 590947a493..836f3987d9 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円233円276円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円233円276円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -34,7 +34,7 @@
一幅图是由**节点**和**边**构成的,逻辑结构如下:
-
+
**什么叫「逻辑结构」?就是说为了方便研究,我们把图抽象成这个样子**。
@@ -64,11 +64,11 @@ class TreeNode {
比如还是刚才那幅图:
-
+
用邻接表和邻接矩阵的存储方式如下:
-
+
邻接表很直观,我把每个节点 `x` 的邻居都存到一个列表里,然后把 `x` 和这个列表关联起来,这样就可以通过一个节点 `x` 找到它的所有相邻节点。
@@ -104,7 +104,7 @@ boolean[][] matrix;
由于有向图的边有方向,所以有向图中每个节点「度」被细分为**入度**(indegree)和**出度**(outdegree),比如下图:
-
+
其中节点 `3` 的入度为 3(有三条边指向它),出度为 1(它有 1 条边指向别的节点)。
@@ -134,7 +134,7 @@ int[][] matrix;
**无向图怎么实现**?也很简单,所谓的「无向」,是不是等同于「双向」?
-
+
如果连接无向图中的节点 `x` 和 `y`,把 `matrix[x][y]` 和 `matrix[y][x]` 都变成 `true` 不就行了;邻接表也是类似的操作,在 `x` 的邻居列表里添加 `y`,同时在 `y` 的邻居列表里添加 `x`。
@@ -189,7 +189,7 @@ void traverse(Graph graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**,类比贪吃蛇游戏,`visited` 记录蛇经过过的格子,而 `onPath` 仅仅记录蛇身。在图的遍历过程中,`onPath` 用于判断是否成环,类比当贪吃蛇自己咬到自己(成环)的场景,这下你可以理解它们二者的区别了吧。
@@ -199,7 +199,7 @@ void traverse(Graph graph, int s) {
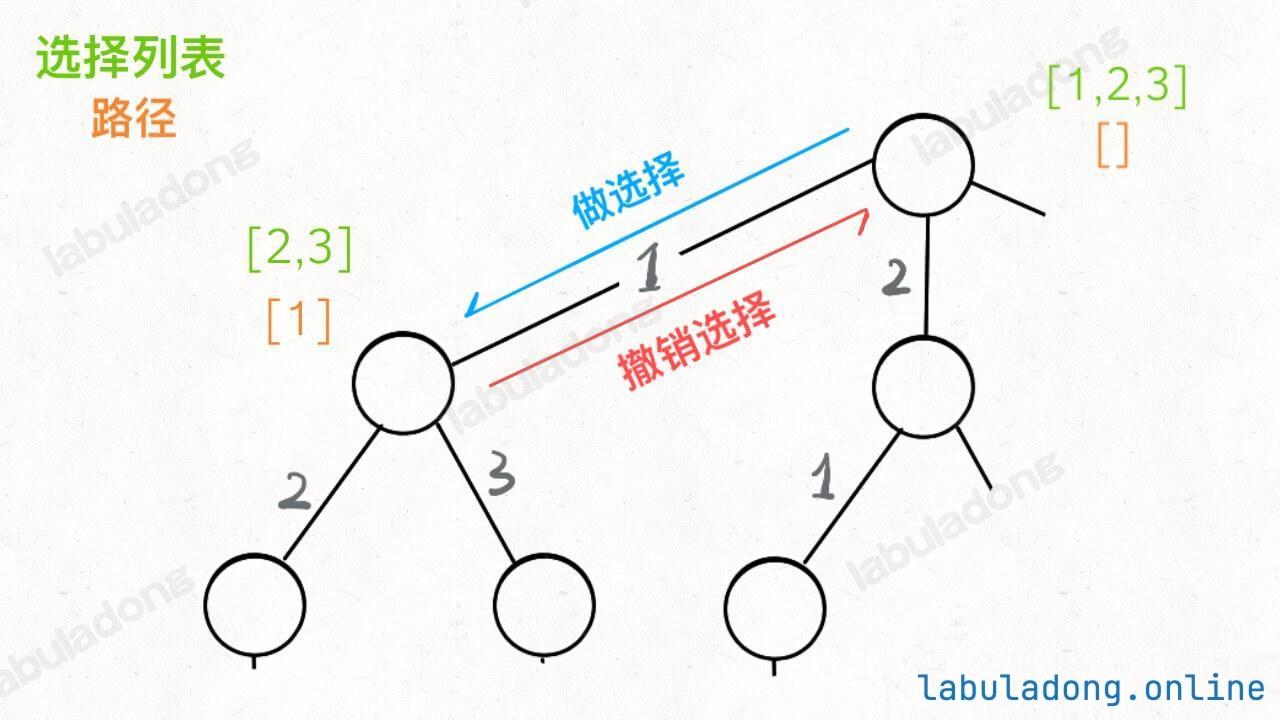
为什么有这个区别呢?这就是前文 [回溯算法核心套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 中讲到的回溯算法和 DFS 算法的区别所在:回溯算法关注的不是节点,而是树枝。不信你看前文画的回溯树,我们需要在「树枝」上做选择和撤销选择:
-
+
他们的区别可以这样反应到代码上:
@@ -260,7 +260,7 @@ List> allPathsSourceTarget(int[][] graph);
比如输入 `graph = [[1,2],[3],[3],[]]`,就代表下面这幅图:
-
+
算法应该返回 `[[0,1,3],[0,2,3]]`,即 `0` 到 `3` 的所有路径。
@@ -329,7 +329,7 @@ void traverse(int[][] graph, int s, LinkedList path) {
- [并查集(Union-Find)算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
@@ -359,4 +359,4 @@ void traverse(int[][] graph, int s, LinkedList path) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円256円236円347円216円260円350円256円241円347円256円227円345円231円250円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円256円236円347円216円260円350円256円241円347円256円227円345円231円250円.md"
index ee96d96214..30e25a90eb 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円256円236円347円216円260円350円256円241円347円256円227円345円231円250円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/345円256円236円347円216円260円350円256円241円347円256円227円345円231円250円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -125,13 +125,13 @@ int calculate(string s) {
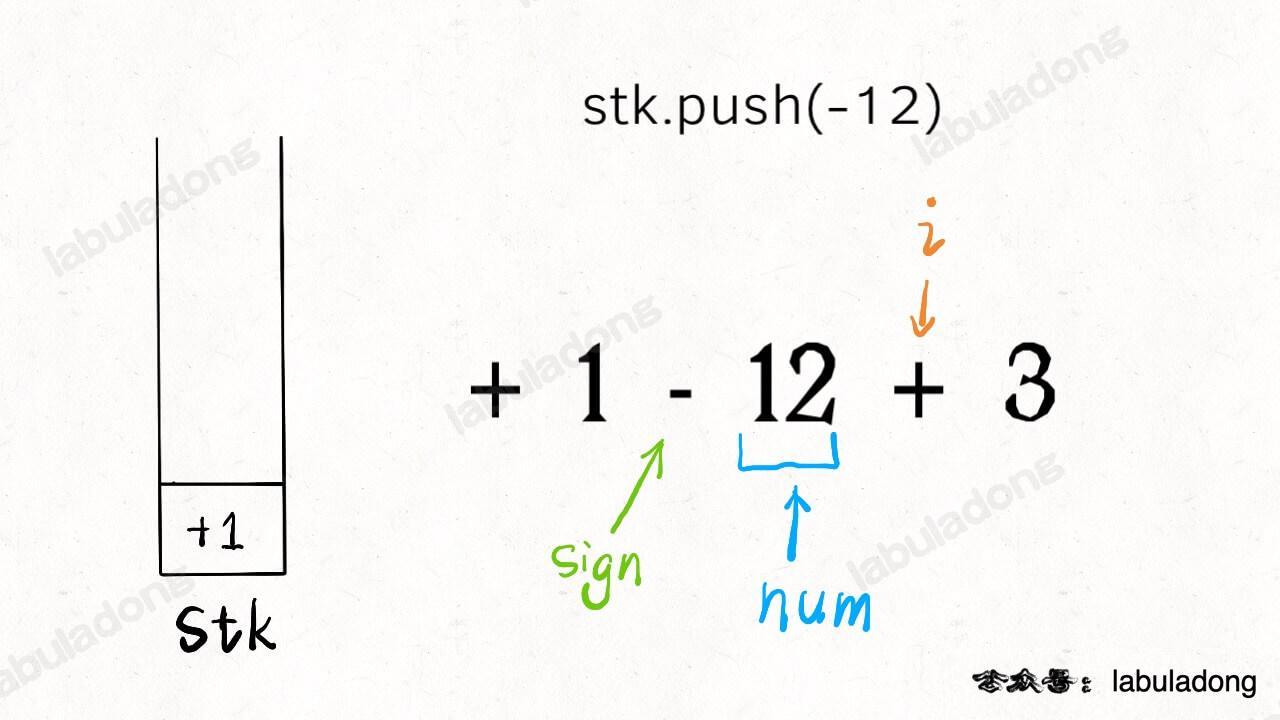
我估计就是中间带 `switch` 语句的部分有点不好理解吧,`i` 就是从左到右扫描,`sign` 和 `num` 跟在它身后。当 `s[i]` 遇到一个运算符时,情况是这样的:
-
+
所以说,此时要根据 `sign` 的 case 不同选择 `nums` 的正负号,存入栈中,然后更新 `sign` 并清零 `nums` 记录下一对儿符合和数字的组合。
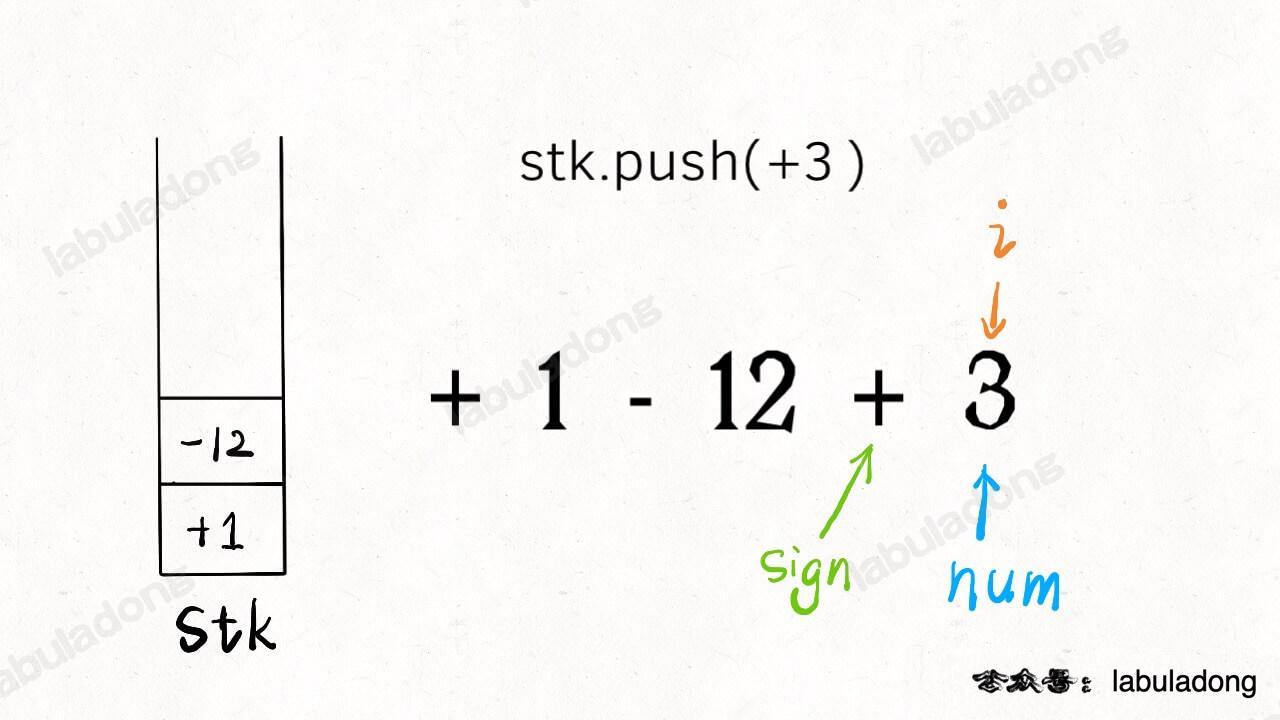
另外注意,不只是遇到新的符号会触发入栈,当 `i` 走到了算式的尽头(`i == s.size() - 1` ),也应该将前面的数字入栈,方便后续计算最终结果。
-
+
至此,仅处理紧凑加减法字符串的算法就完成了,请确保理解以上内容,后续的内容就基于这个框架修修改改就完事儿了。
@@ -173,7 +173,7 @@ for (int i = 0; i < s.size(); i++) { } ``` -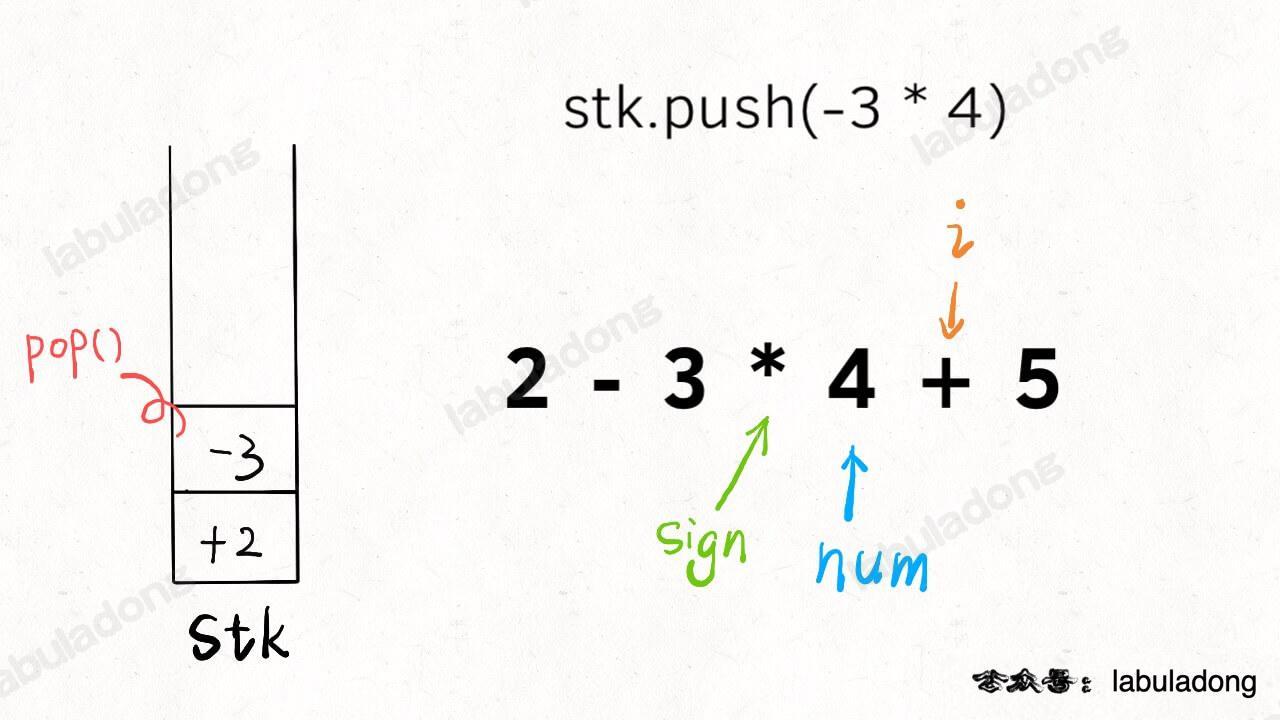 + **乘除法优先于加减法体现在,乘除法可以和栈顶的数结合,而加减法只能把自己放入栈**。 @@ -287,11 +287,11 @@ def calculate(s: str) -> int:
return helper(collections.deque(s))
```
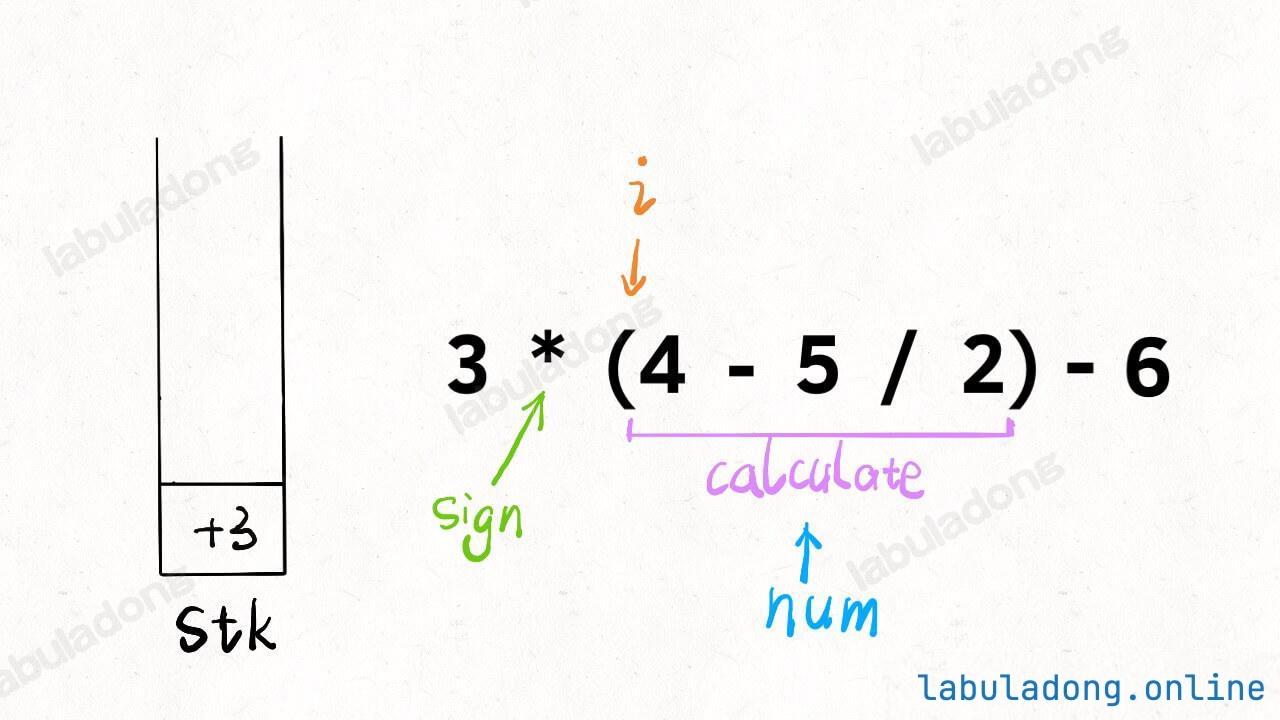
-
+
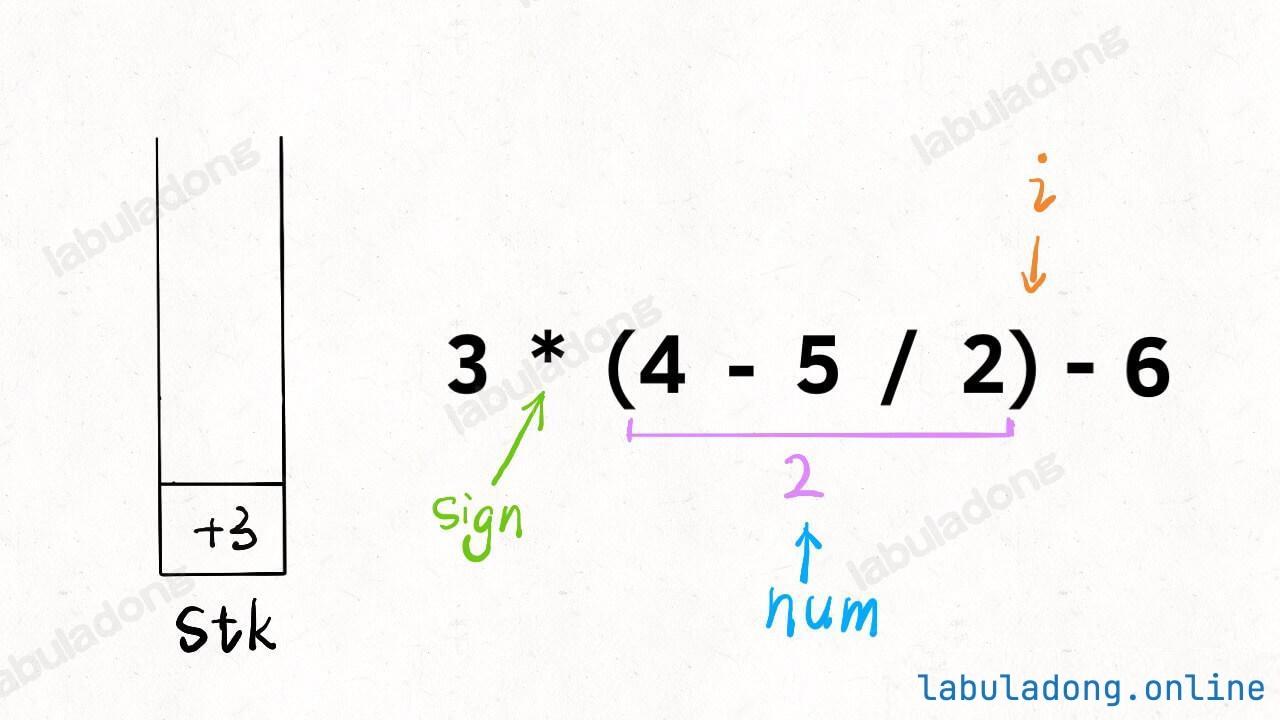
-
+
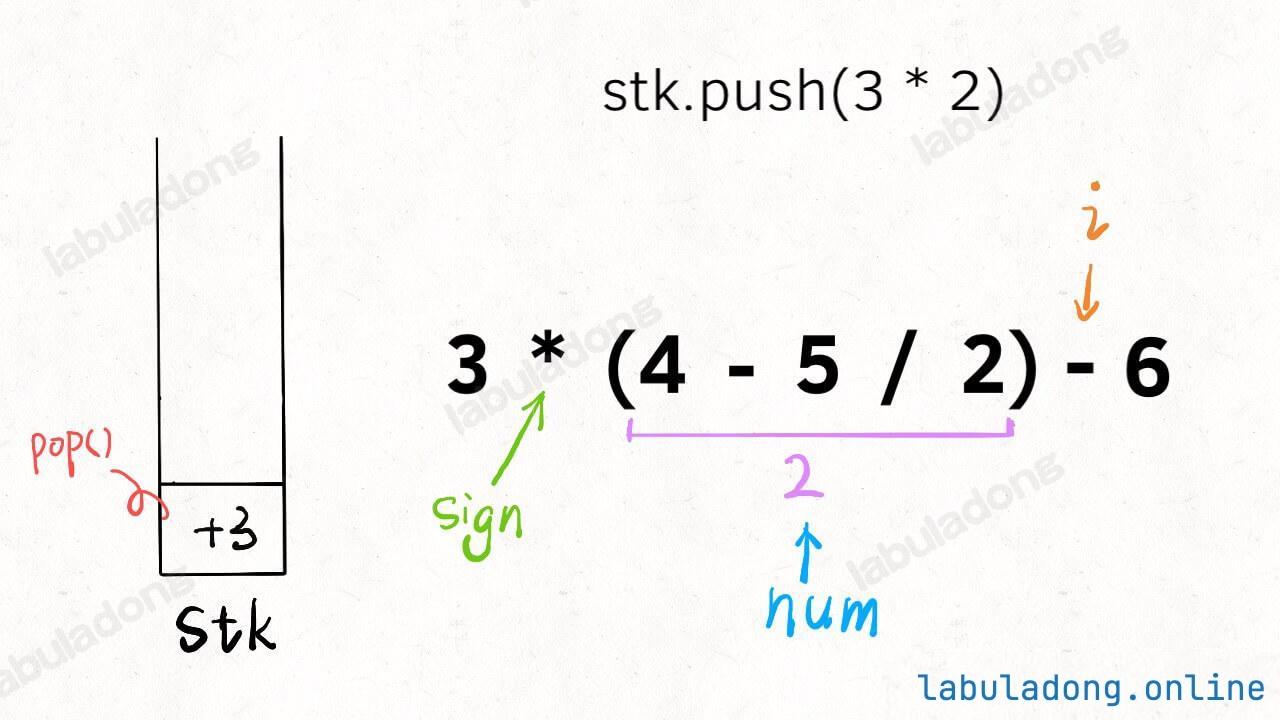
-
+
你看,加了两三行代码,就可以处理括号了,这就是递归的魅力。至此,计算器的全部功能就实现了,通过对问题的层层拆解化整为零,再回头看,这个问题似乎也没那么复杂嘛。
@@ -323,7 +323,7 @@ def calculate(s: str) -> int:
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/346円213円223円346円211円221円346円216円222円345円272円217円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/346円213円223円346円211円221円346円216円222円345円272円217円.md"
index 03e2168ea6..3a1c702876 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/346円213円223円346円211円221円346円216円222円345円272円217円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/346円213円223円346円211円221円346円216円222円345円272円217円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -37,7 +37,7 @@
先来看看力扣第 207 题「课程表」:
-
+
函数签名如下:
@@ -57,7 +57,7 @@ boolean canFinish(int numCourses, int[][] prerequisites);
所以我们可以根据题目输入的 `prerequisites` 数组生成一幅类似这样的图:
-
+
**如果发现这幅有向图中存在环,那就说明课程之间存在循环依赖,肯定没办法全部上完;反之,如果没有环,那么肯定能上完全部课程**。
@@ -178,7 +178,7 @@ void traverse(List[] graph, int s) {
注意 `visited` 数组和 `onPath` 数组的区别,因为二叉树算是特殊的图,所以用遍历二叉树的过程来理解下这两个数组的区别:
-
+
**上述 GIF 描述了递归遍历二叉树的过程,在 `visited` 中被标记为 true 的节点用灰色表示,在 `onPath` 中被标记为 true 的节点用绿色表示**。
@@ -241,7 +241,7 @@ List[] buildGraph(int numCourses, int[][] prerequisites) {
不是的,假设下图中绿色的节点是递归的路径,它们在 `onPath` 中的值都是 true,但显然成环的节点只是其中的一部分:
-
+
这个问题留给大家思考,我会在公众号留言区置顶正确的答案。
@@ -251,7 +251,7 @@ List[] buildGraph(int numCourses, int[][] prerequisites) {
看下力扣第 210 题「课程表 II」:
-
+
这道题就是上道题的进阶版,不是仅仅让你判断是否可以完成所有课程,而是进一步让你返回一个合理的上课顺序,保证开始修每个课程时,前置的课程都已经修完。
@@ -263,7 +263,7 @@ int[] findOrder(int numCourses, int[][] prerequisites);
这里我先说一下拓扑排序(Topological Sorting)这个名词,网上搜出来的定义很数学,这里干脆用百度百科的一幅图来让你直观地感受下:
-
+
> PS:图片中拓扑排序的结果有误,`C7->C8->C6` 应该改为 `C6->C7->C8`。
@@ -378,13 +378,13 @@ void traverse(TreeNode root) {
你把二叉树理解成一幅有向图,边的方向是由父节点指向子节点,那么就是下图这样:
-
+
按照我们的定义,边的含义是「被依赖」关系,那么上图的拓扑排序应该首先是节点 `1`,然后是 `2, 3`,以此类推。
但显然标准的后序遍历结果不满足拓扑排序,而如果把后序遍历结果反转,就是拓扑排序结果了:
-
+
以上,我直观解释了一下为什么「拓扑排序的结果就是反转之后的后序遍历结果」,当然,我的解释并没有严格的数学证明,有兴趣的读者可以自己查一下。
@@ -462,27 +462,27 @@ List[] buildGraph(int n, int[][] edges) {
我画个图你就容易理解了,比如下面这幅图,节点中的数字代表该节点的入度:
-
+
队列进行初始化后,入度为 0 的节点首先被加入队列:
-
+
开始执行 BFS 循环,从队列中弹出一个节点,减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-
+
继续从队列弹出节点,并减少相邻节点的入度,这一次没有新产生的入度为 0 的节点:
-
+
继续从队列弹出节点,并减少相邻节点的入度,同时将新产生的入度为 0 的节点加入队列:
-
+
继续弹出节点,直到队列为空:
-
+
这时候,所有节点都被遍历过一遍,也就说明图中不存在环。
@@ -490,11 +490,11 @@ List[] buildGraph(int n, int[][] edges) {
比如下面这种情况,队列中最初只有一个入度为 0 的节点:
-
+
当弹出这个节点并减小相邻节点的入度之后队列为空,但并没有产生新的入度为 0 的节点加入队列,所以 BFS 算法终止:
-
+
你看到了,如果存在节点没有被遍历,那么说明图中存在环,现在回头去看 BFS 的代码,你应该就很容易理解其中的逻辑了。
@@ -504,7 +504,7 @@ List[] buildGraph(int n, int[][] edges) {
比如刚才举的第一个例子,下图每个节点中的值即入队的顺序:
-
+
显然,这个顺序就是一个可行的拓扑排序结果。
@@ -581,7 +581,7 @@ List[] buildGraph(int n, int[][] edges) {
- [图论基础及遍历算法](https://labuladong.github.io/article/fname.html?fname=图)
- [并查集(Union-Find)算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
@@ -606,4 +606,4 @@ List[] buildGraph(int n, int[][] edges) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/350円256円276円350円256円241円Twitter.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/350円256円276円350円256円241円Twitter.md"
index 93e98455a4..7d8d435df1 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/350円256円276円350円256円241円Twitter.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/350円256円276円350円256円241円Twitter.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -123,13 +123,13 @@ class Tweet {
}
```
-
+
**2、User 类的实现**
我们根据实际场景想一想,一个用户需要存储的信息有 userId,关注列表,以及该用户发过的推文列表。其中关注列表应该用集合(Hash Set)这种数据结构来存,因为不能重复,而且需要快速查找;推文列表应该由链表这种数据结构储存,以便于进行有序合并的操作。画个图理解一下:
-
+
除此之外,根据面向对象的设计原则,「关注」「取关」和「发文」应该是 User 的行为,况且关注列表和推文列表也存储在 User 类中,所以我们也应该给 User 添加 follow,unfollow 和 post 这几个方法:
@@ -272,7 +272,7 @@ public List getNewsFeed(int userId) {
这个过程是这样的,下面是我制作的一个 GIF 图描述合并链表的过程。假设有三个 Tweet 链表按 time 属性降序排列,我们把他们降序合并添加到 res 中。注意图中链表节点中的数字是 time 属性,不是 id 属性:
-
+
至此,这道一个极其简化的 Twitter 时间线功能就设计完毕了。
@@ -284,7 +284,7 @@ public List getNewsFeed(int userId) {
当然,实际应用中的社交 App 数据量是巨大的,考虑到数据库的读写性能,我们的设计可能承受不住流量压力,还是有些太简化了。而且实际的应用都是一个极其庞大的工程,比如下图,是 Twitter 这样的社交网站大致的系统结构:
-
+
我们解决的问题应该只能算 Timeline Service 模块的一小部分,功能越多,系统的复杂性可能是指数级增长的。所以说合理的顶层设计十分重要,其作用是远超某一个算法的。Github 上有一个优秀的开源项目,专门收集了很多大型系统设计的案例和解析,而且有中文版本,上面这个图也出自该项目。对系统设计感兴趣的读者可以点击 [这里](https://github.com/donnemartin/system-design-primer) 查看。
@@ -308,7 +308,7 @@ public List getNewsFeed(int userId) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円200円222円345円275円222円345円217円215円350円275円254円351円223円276円350円241円250円347円232円204円344円270円200円351円203円250円345円210円206円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円200円222円345円275円222円345円217円215円350円275円254円351円223円276円350円241円250円347円232円204円344円270円200円351円203円250円345円210円206円.md"
index 5a225b5475..34f553d345 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円200円222円345円275円222円345円217円215円350円275円254円351円223円276円350円241円250円347円232円204円344円270円200円351円203円250円345円210円206円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円200円222円345円275円222円345円217円215円350円275円254円351円223円276円350円241円250円347円232円204円344円270円200円351円203円250円345円210円206円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -41,7 +41,7 @@ public class ListNode {
看下力扣第 92 题「反转链表 II」:
-
+
**注意这里的索引是从 1 开始的**。迭代的思路大概是:先用一个 for 循环找到第 `m` 个位置,然后再用一个 for 循环将 `m` 和 `n` 之间的元素反转。但是我们的递归解法不用一个 for 循环,纯递归实现反转。
@@ -72,7 +72,7 @@ ListNode reverse(ListNode head) {
明白了函数的定义,再来看这个问题。比如说我们想反转这个链表:
-
+
那么输入 `reverse(head)` 后,会在这里进行递归:
@@ -82,11 +82,11 @@ ListNode last = reverse(head.next);
不要跳进递归(你的脑袋能压几个栈呀?),而是要根据刚才的函数定义,来弄清楚这段代码会产生什么结果:
-
+
这个 `reverse(head.next)` 执行完成后,整个链表就成了这样:
-
+
并且根据函数定义,`reverse` 函数会返回反转之后的头结点,我们用变量 `last` 接收了。
@@ -96,7 +96,7 @@ ListNode last = reverse(head.next);
head.next.next = head;
```
-
+
接下来:
@@ -105,7 +105,7 @@ head.next = null;
return last;
```
-
+
神不神奇,这样整个链表就反转过来了!递归代码就是这么简洁优雅,不过其中有两个地方需要注意:
@@ -138,7 +138,7 @@ ListNode reverseN(ListNode head, int n)
比如说对于下图链表,执行 `reverseN(head, 3)`:
-
+
解决思路和反转整个链表差不多,只要稍加修改即可:
@@ -168,7 +168,7 @@ ListNode reverseN(ListNode head, int n) {
2、刚才我们直接把 `head.next` 设置为 null,因为整个链表反转后原来的 `head` 变成了整个链表的最后一个节点。但现在 `head` 节点在递归反转之后不一定是最后一个节点了,所以要记录后驱 `successor`(第 `n + 1` 个节点),反转之后将 `head` 连接上。
-
+
OK,如果这个函数你也能看懂,就离实现「反转一部分链表」不远了。
@@ -254,7 +254,7 @@ ListNode reverseBetween(ListNode head, int m, int n) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円230円237円345円210円227円345円256円236円347円216円260円346円240円210円346円240円210円345円256円236円347円216円260円351円230円237円345円210円227円.md" "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円230円237円345円210円227円345円256円236円347円216円260円346円240円210円346円240円210円345円256円236円347円216円260円351円230円237円345円210円227円.md"
index d945f1ba0e..55a47cb5e0 100644
--- "a/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円230円237円345円210円227円345円256円236円347円216円260円346円240円210円346円240円210円345円256円236円347円216円260円351円230円237円345円210円227円.md"
+++ "b/346円225円260円346円215円256円347円273円223円346円236円204円347円263円273円345円210円227円/351円230円237円345円210円227円345円256円236円347円216円260円346円240円210円346円240円210円345円256円236円347円216円260円351円230円237円345円210円227円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
队列是一种先进先出的数据结构,栈是一种先进后出的数据结构,形象一点就是这样:
-
+
这两种数据结构底层其实都是数组或者链表实现的,只是 API 限定了它们的特性,那么今天就来看看如何使用「栈」的特性来实现一个「队列」,如何用「队列」实现一个「栈」。
@@ -52,7 +52,7 @@ class MyQueue {
我们使用两个栈 `s1, s2` 就能实现一个队列的功能(这样放置栈可能更容易理解):
-
+
```java
class MyQueue {
@@ -68,7 +68,7 @@ class MyQueue {
当调用 `push` 让元素入队时,只要把元素压入 `s1` 即可,比如说 `push` 进 3 个元素分别是 1,2,3,那么底层结构就是这样:
-
+
```java
/** 添加元素到队尾 */
@@ -79,7 +79,7 @@ public void push(int x) {
那么如果这时候使用 `peek` 查看队头的元素怎么办呢?按道理队头元素应该是 1,但是在 `s1` 中 1 被压在栈底,现在就要轮到 `s2` 起到一个中转的作用了:当 `s2` 为空时,可以把 `s1` 的所有元素取出再添加进 `s2`,**这时候 `s2` 中元素就是先进先出顺序了**。
-
+
```java
/** 返回队头元素 */
@@ -166,11 +166,11 @@ class MyStack {
我们的底层数据结构是先进先出的队列,每次 `pop` 只能从队头取元素;但是栈是后进先出,也就是说 `pop` API 要从队尾取元素:
-
+
解决方法简单粗暴,把队列前面的都取出来再加入队尾,让之前的队尾元素排到队头,这样就可以取出了:
-
+
```java
/** 删除栈顶的元素并返回 */
@@ -217,7 +217,7 @@ public boolean empty() {
个人认为,用队列实现栈是没啥亮点的问题,但是**用双栈实现队列是值得学习的**。
-
+
从栈 `s1` 搬运元素到 `s2` 之后,元素在 `s2` 中就变成了队列的先进先出顺序,这个特性有点类似「负负得正」,确实不太容易想到。
@@ -244,7 +244,7 @@ public boolean empty() {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS346円241円206円346円236円266円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS346円241円206円346円236円266円.md"
index 6947ca8dbc..fb79225f6c 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS346円241円206円346円236円266円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS346円241円206円346円236円266円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -49,7 +49,7 @@ BFS 相对 DFS 的最主要的区别是:**BFS 找到的路径一定是最短
净整些花里胡哨的,这些问题都没啥奇技淫巧,本质上就是一幅「图」,让你从一个起点,走到终点,问最短路径。这就是 BFS 的本质,框架搞清楚了直接默写就好。
-
+
记住下面这个框架就 OK 了:
@@ -91,7 +91,7 @@ int BFS(Node start, Node target) {
先来个简单的问题实践一下 BFS 框架吧,判断一棵二叉树的**最小**高度,这也是力扣第 111 题「二叉树的最小深度」:
-
+
怎么套到 BFS 的框架里呢?首先明确一下起点 `start` 和终点 `target` 是什么,怎么判断到达了终点?
@@ -135,7 +135,7 @@ int minDepth(TreeNode root) {
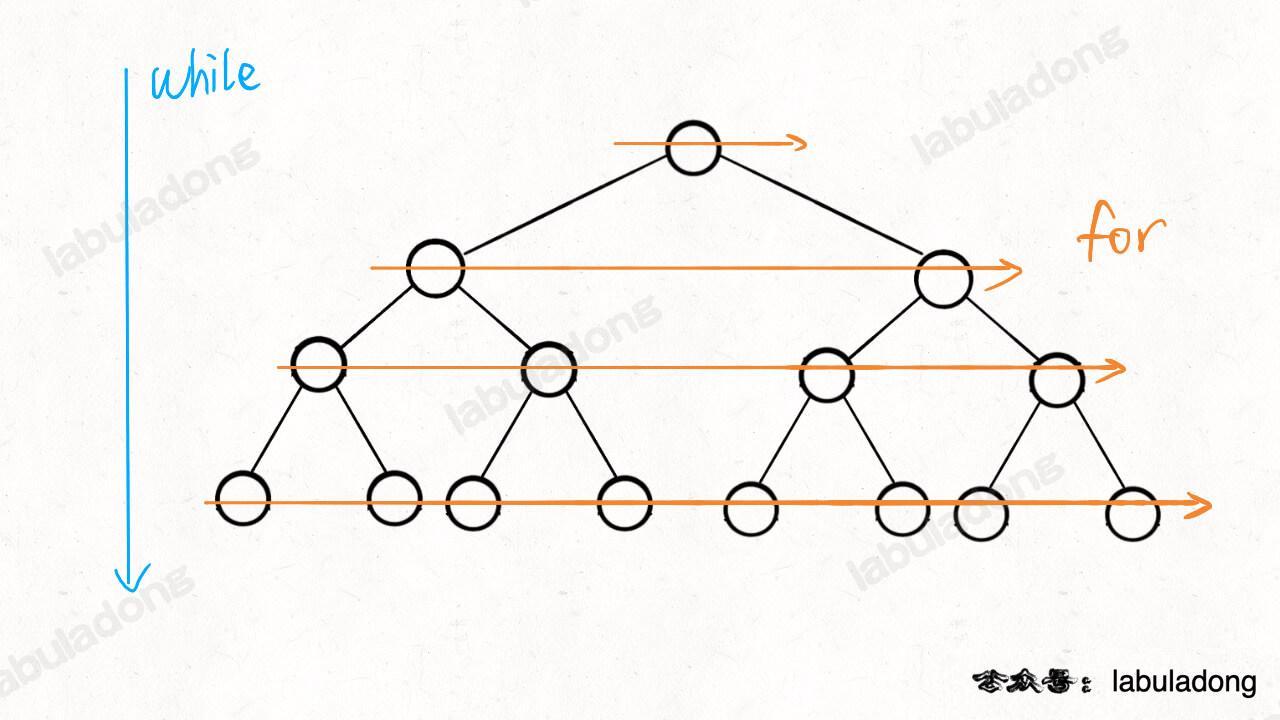
这里注意这个 `while` 循环和 `for` 循环的配合,**`while` 循环控制一层一层往下走,`for` 循环利用 `sz` 变量控制从左到右遍历每一层二叉树节点**:
-
+
这一点很重要,这个形式在普通 BFS 问题中都很常见,但是在 [Dijkstra 算法模板框架](https://labuladong.github.io/article/fname.html?fname=dijkstra算法) 中我们修改了这种代码模式,读完并理解本文后你可以去看看 BFS 算法是如何演变成 Dijkstra 算法在加权图中寻找最短路径的。
@@ -165,7 +165,7 @@ BFS 可以找到最短距离,但是空间复杂度高,而 DFS 的空间复
这是力扣第 752 题「打开转盘锁」,比较有意思:
-
+
题目中描述的就是我们生活中常见的那种密码锁,如果没有任何约束,最少的拨动次数很好算,就像我们平时开密码锁那样直奔密码拨就行了。
@@ -295,9 +295,9 @@ int openLock(String[] deadends, String target) {
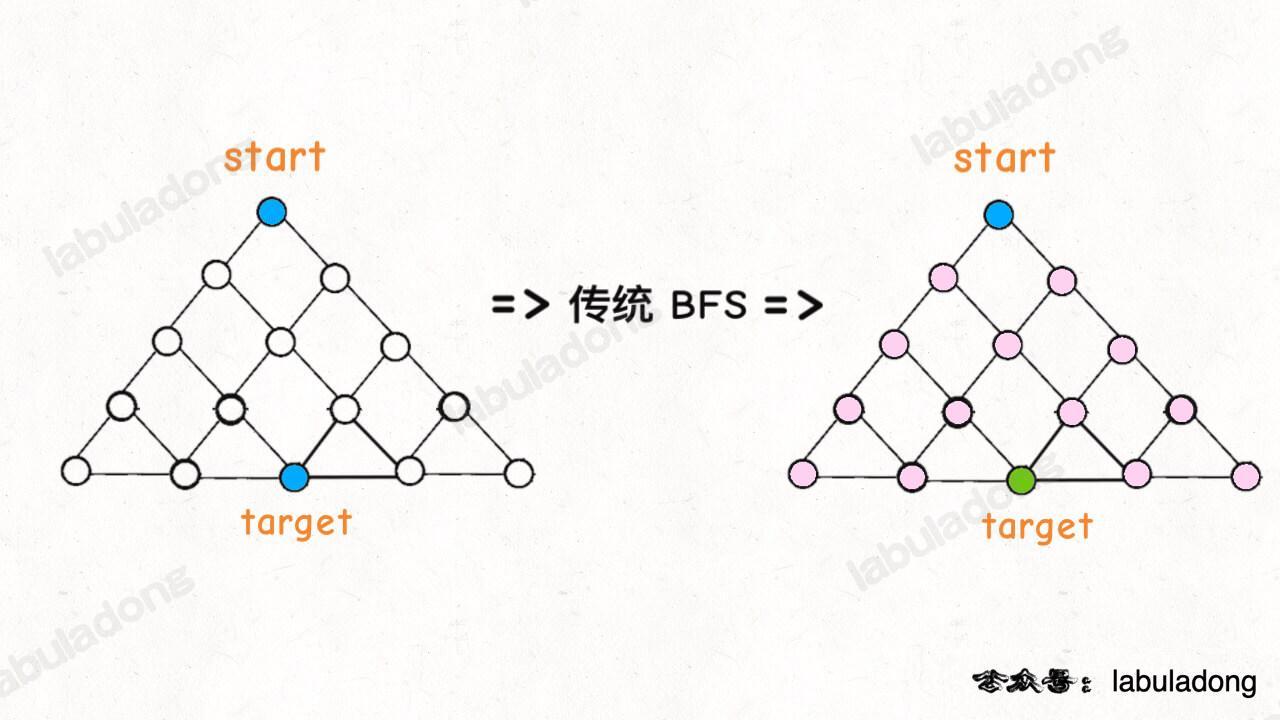
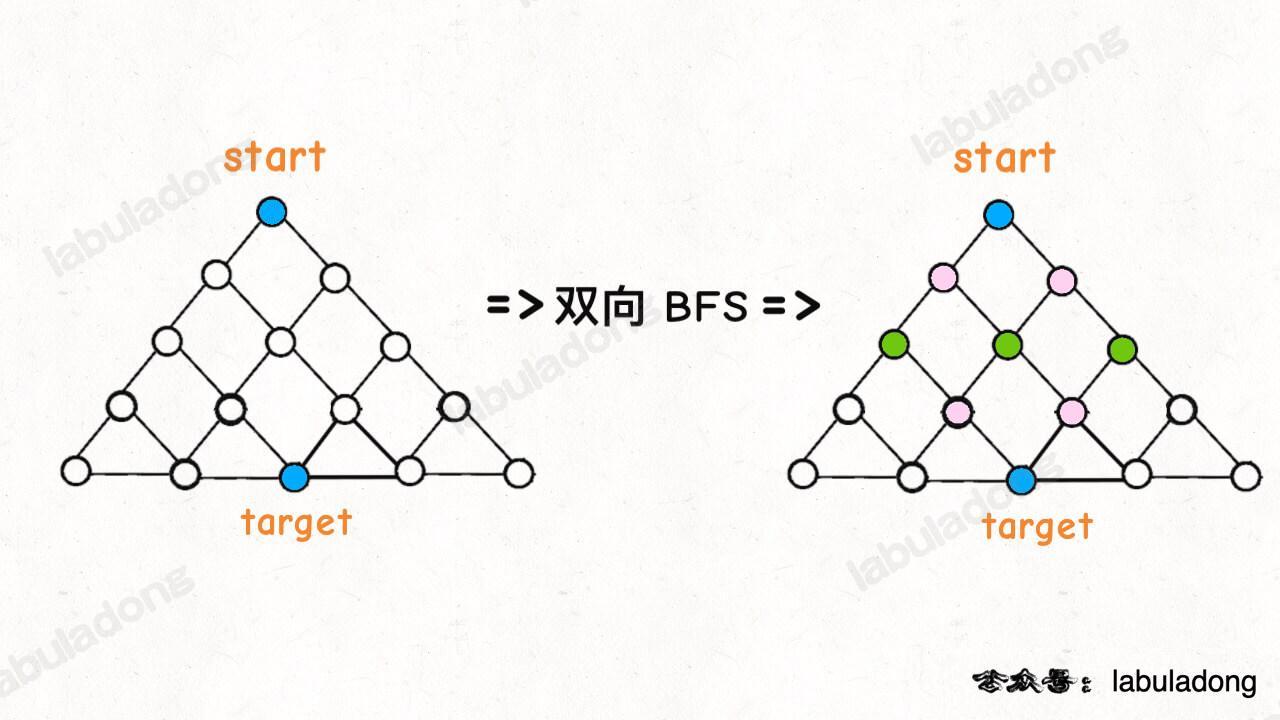
为什么这样能够能够提升效率呢?其实从 Big O 表示法分析算法复杂度的话,它俩的最坏复杂度都是 `O(N)`,但是实际上双向 BFS 确实会快一些,我给你画两张图看一眼就明白了:
-
+
-
+
图示中的树形结构,如果终点在最底部,按照传统 BFS 算法的策略,会把整棵树的节点都搜索一遍,最后找到 `target`;而双向 BFS 其实只遍历了半棵树就出现了交集,也就是找到了最短距离。从这个例子可以直观地感受到,双向 BFS 是要比传统 BFS 高效的。
@@ -395,7 +395,7 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- [旅游省钱大法:加权最短路径](https://labuladong.github.io/article/fname.html?fname=旅行最短路径)
- [环检测及拓扑排序算法](https://labuladong.github.io/article/fname.html?fname=拓扑排序)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
- [算法学习和心流体验](https://labuladong.github.io/article/fname.html?fname=心流)
@@ -429,4 +429,4 @@ while (!q1.isEmpty() && !q2.isEmpty()) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS350円247円243円345円206円263円346円273円221円345円212円250円346円213円274円345円233円276円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS350円247円243円345円206円263円346円273円221円345円212円250円346円213円274円345円233円276円.md"
index 2acefba743..c8b16e3a86 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS350円247円243円345円206円263円346円273円221円345円212円250円346円213円274円345円233円276円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/BFS350円247円243円345円206円263円346円273円221円345円212円250円346円213円274円345円233円276円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -23,13 +23,13 @@
滑动拼图游戏大家应该都玩过,下图是一个 4x4 的滑动拼图:
-
+
拼图中有一个格子是空的,可以利用这个空着的格子移动其他数字。你需要通过移动这些数字,得到某个特定排列顺序,这样就算赢了。
我小时候还玩过一款叫做「华容道」的益智游戏,也和滑动拼图比较类似:
-
+
实际上,滑动拼图游戏也叫数字华容道,你看它俩挺相似的。
@@ -45,7 +45,7 @@
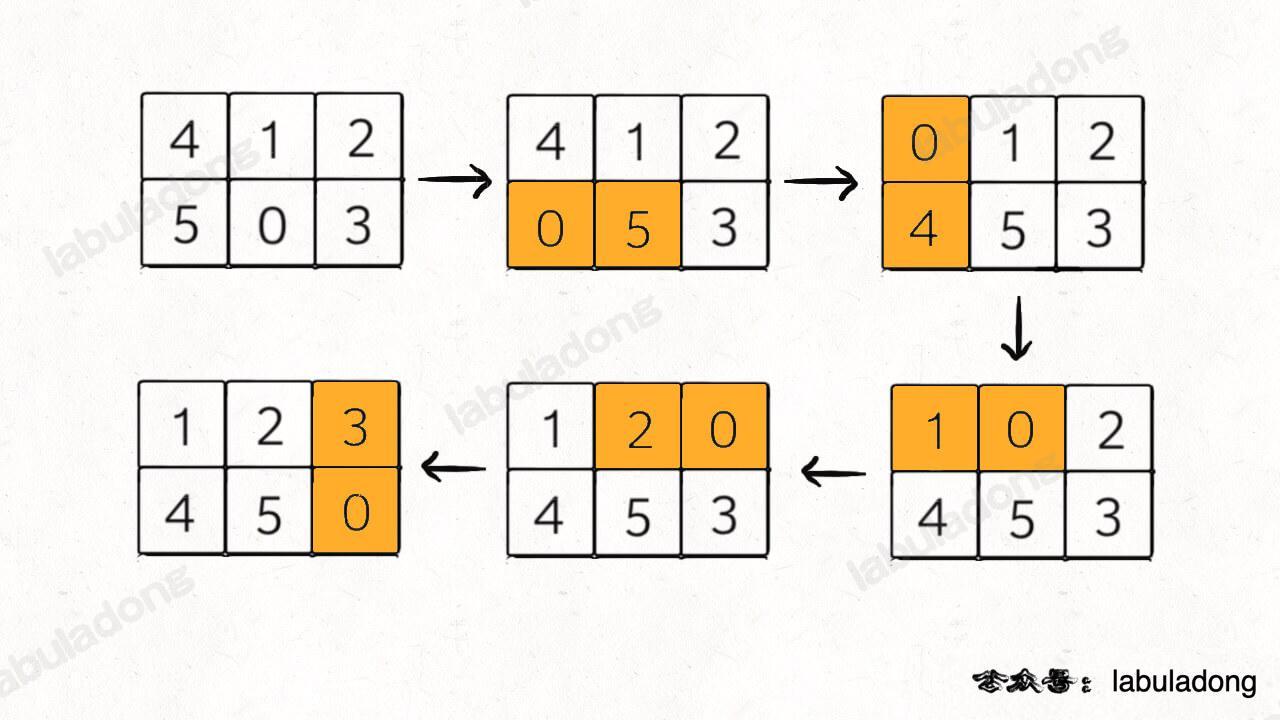
比如说输入的二维数组 `board = [[4,1,2],[5,0,3]]`,算法应该返回 5:
-
+
如果输入的是 `board = [[1,2,3],[5,4,0]]`,则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
@@ -65,7 +65,7 @@
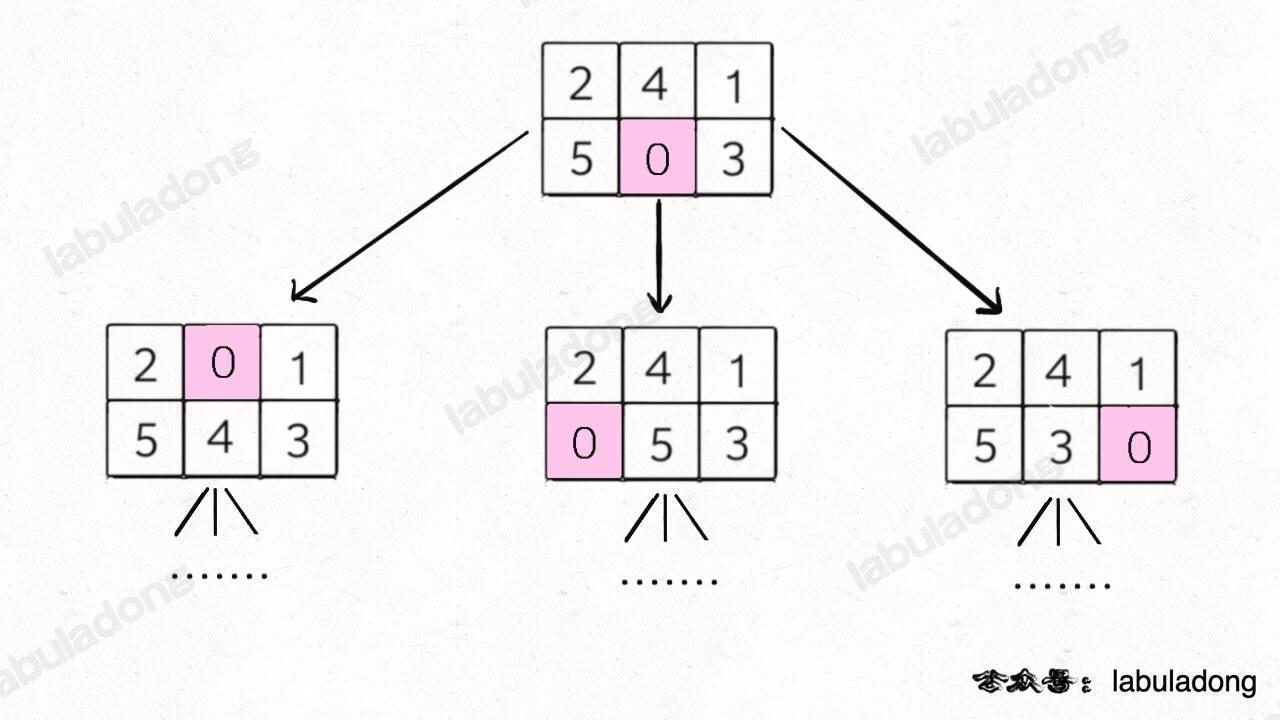
明白了这个道理,我们的问题就转化成了:**如何穷举出 `board` 当前局面下可能衍生出的所有局面**?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
-
+
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列...... 当第一次到达 `target` 时,就得到了赢得游戏的最少步数。
@@ -87,7 +87,7 @@ int[][] neighbor = new int[][]{
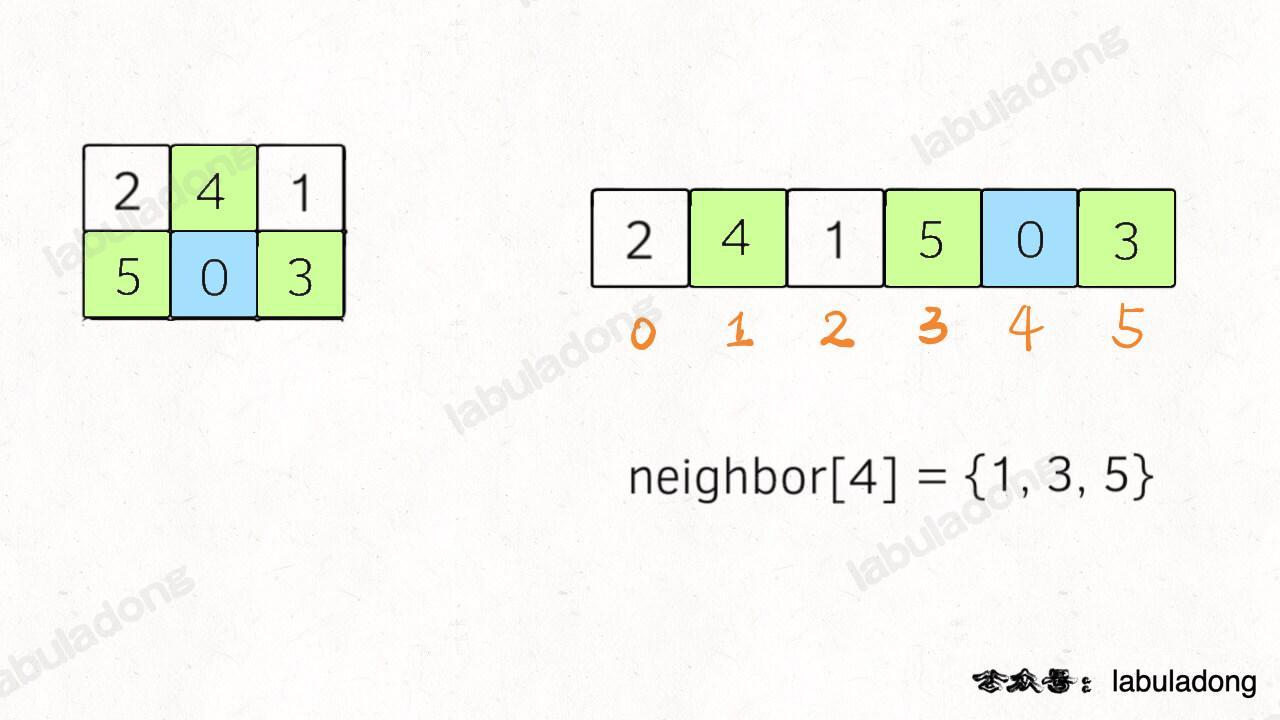
**这个含义就是,在一维字符串中,索引 `i` 在二维数组中的的相邻索引为 `neighbor[i]`**:
-
+
那么对于一个 `m x n` 的二维数组,手写它的一维索引映射肯定不现实了,如何用代码生成它的一维索引映射呢?
@@ -185,4 +185,4 @@ private String swap(char[] chars, int i, int j) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/UnionFind347円256円227円346円263円225円350円257円246円350円247円243円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/UnionFind347円256円227円346円263円225円350円257円246円350円247円243円.md"
index 0b4d8f4119..7a5d710255 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/UnionFind347円256円227円346円263円225円350円257円246円350円247円243円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/UnionFind347円256円227円346円263円225円350円257円246円350円247円243円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -43,7 +43,7 @@
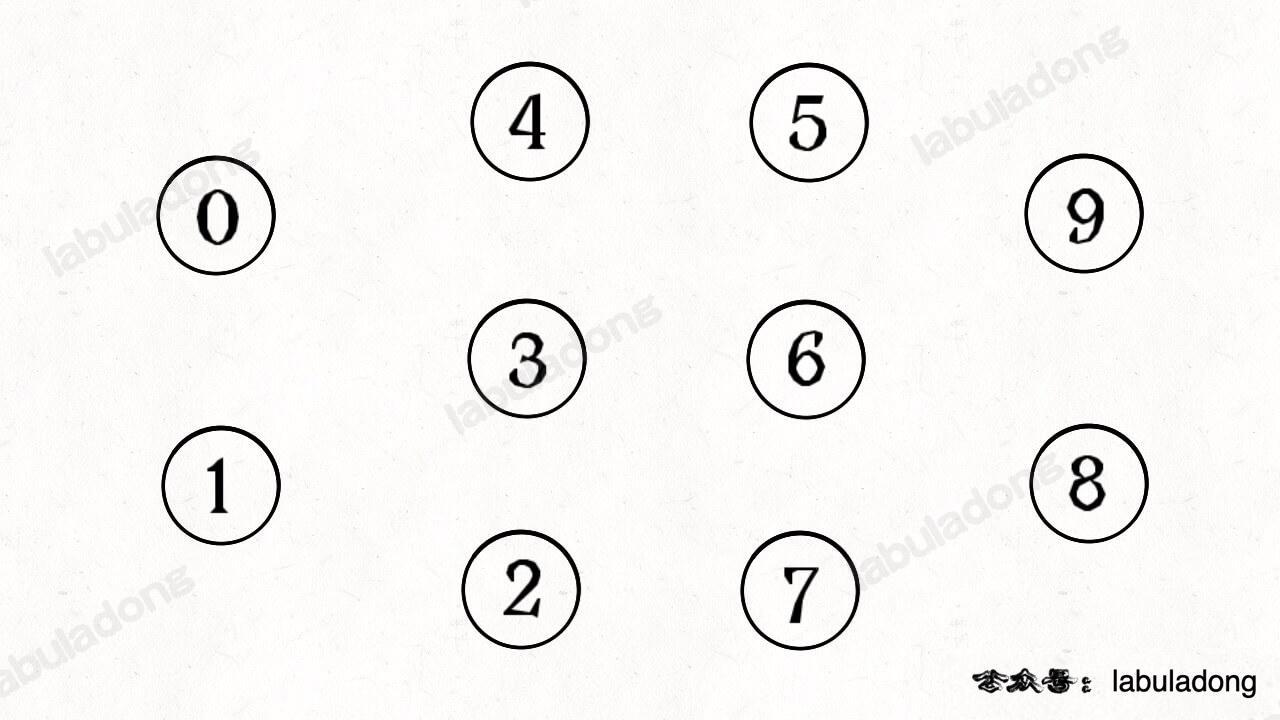
简单说,动态连通性其实可以抽象成给一幅图连线。比如下面这幅图,总共有 10 个节点,他们互不相连,分别用 0~9 标记:
-
+
现在我们的 Union-Find 算法主要需要实现这两个 API:
@@ -72,7 +72,7 @@ class UF {
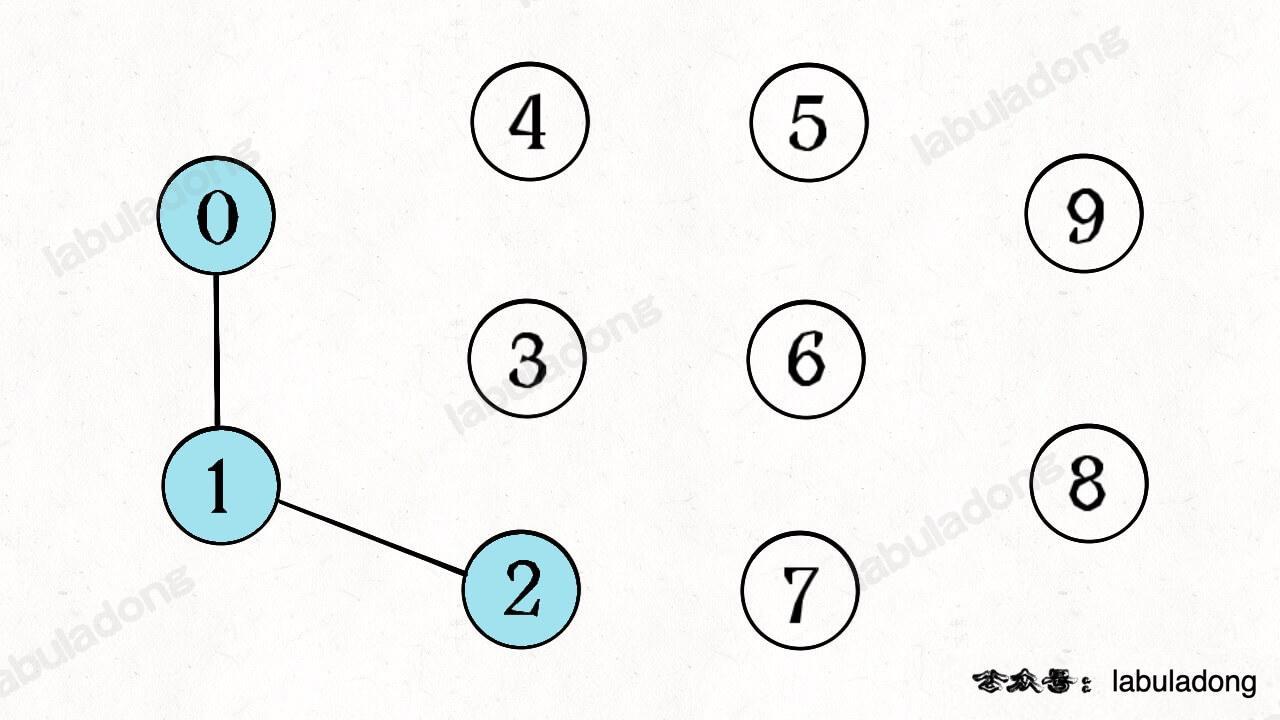
再调用 `union(1, 2)`,这时 0,1,2 都被连通,调用 `connected(0, 2)` 也会返回 true,连通分量变为 8 个。
-
+
判断这种「等价关系」非常实用,比如说编译器判断同一个变量的不同引用,比如社交网络中的朋友圈计算等等。
@@ -84,7 +84,7 @@ class UF {
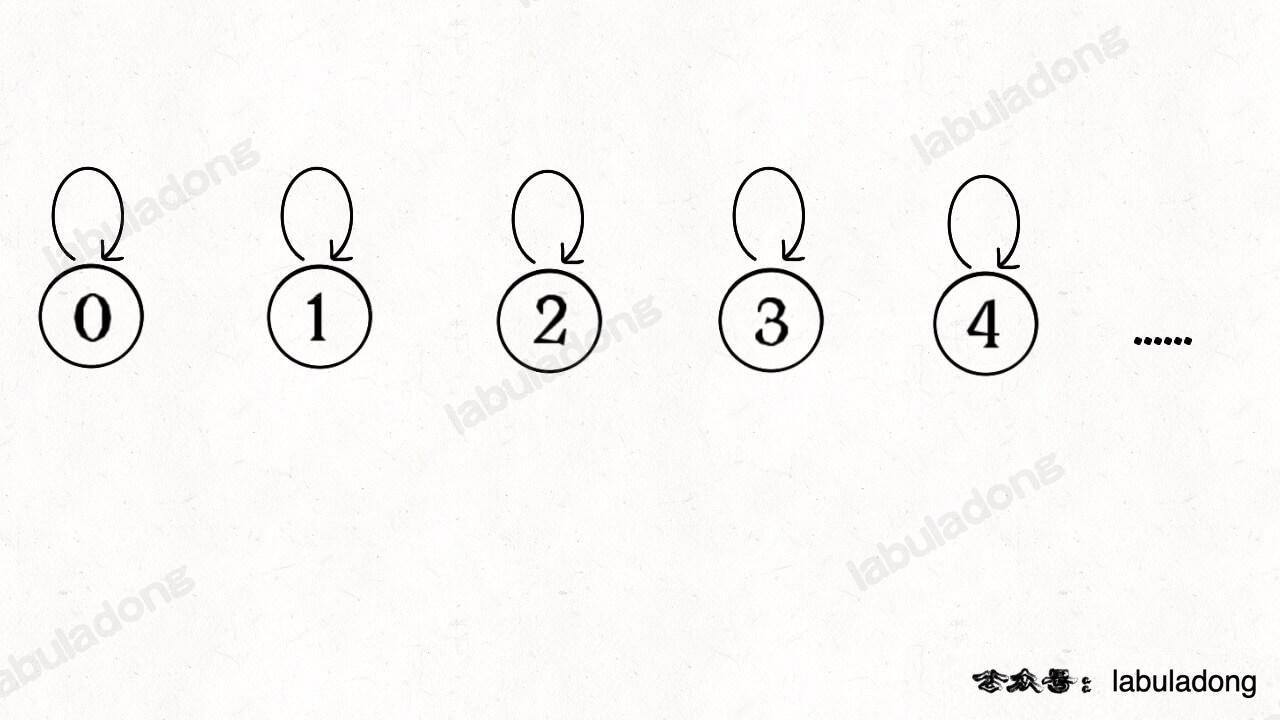
怎么用森林来表示连通性呢?我们设定树的每个节点有一个指针指向其父节点,如果是根节点的话,这个指针指向自己。比如说刚才那幅 10 个节点的图,一开始的时候没有相互连通,就是这样:
-
+
```java
class UF {
@@ -109,7 +109,7 @@ class UF {
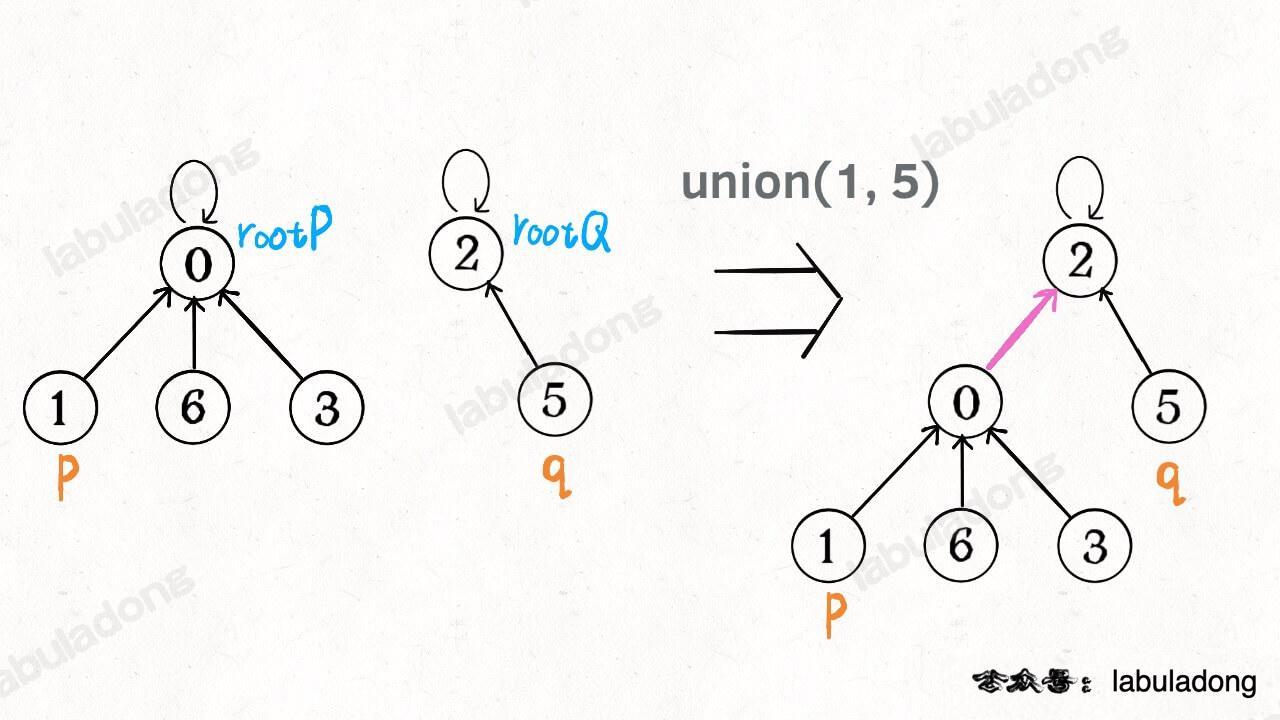
**如果某两个节点被连通,则让其中的(任意)一个节点的根节点接到另一个节点的根节点上**:
-
+
```java
public void union(int p, int q) {
@@ -139,7 +139,7 @@ public int count() {
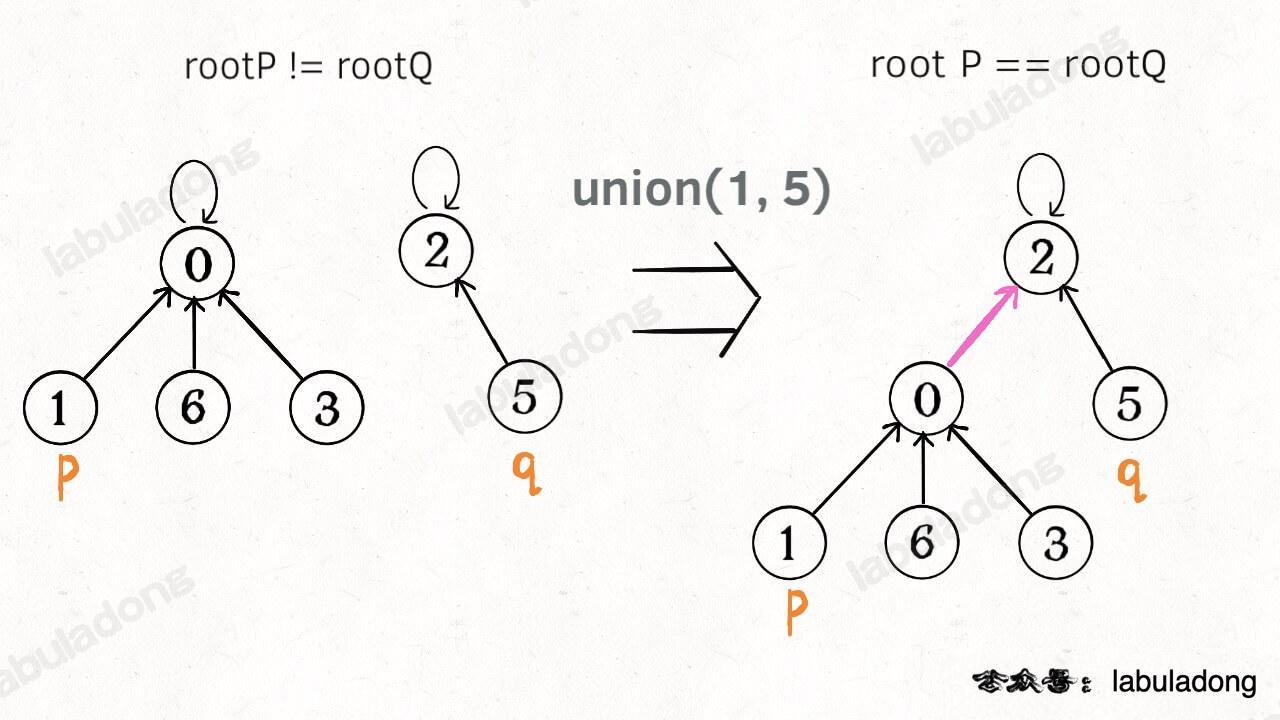
**这样,如果节点 `p` 和 `q` 连通的话,它们一定拥有相同的根节点**:
-
+
```java
public boolean connected(int p, int q) {
@@ -155,7 +155,7 @@ public boolean connected(int p, int q) {
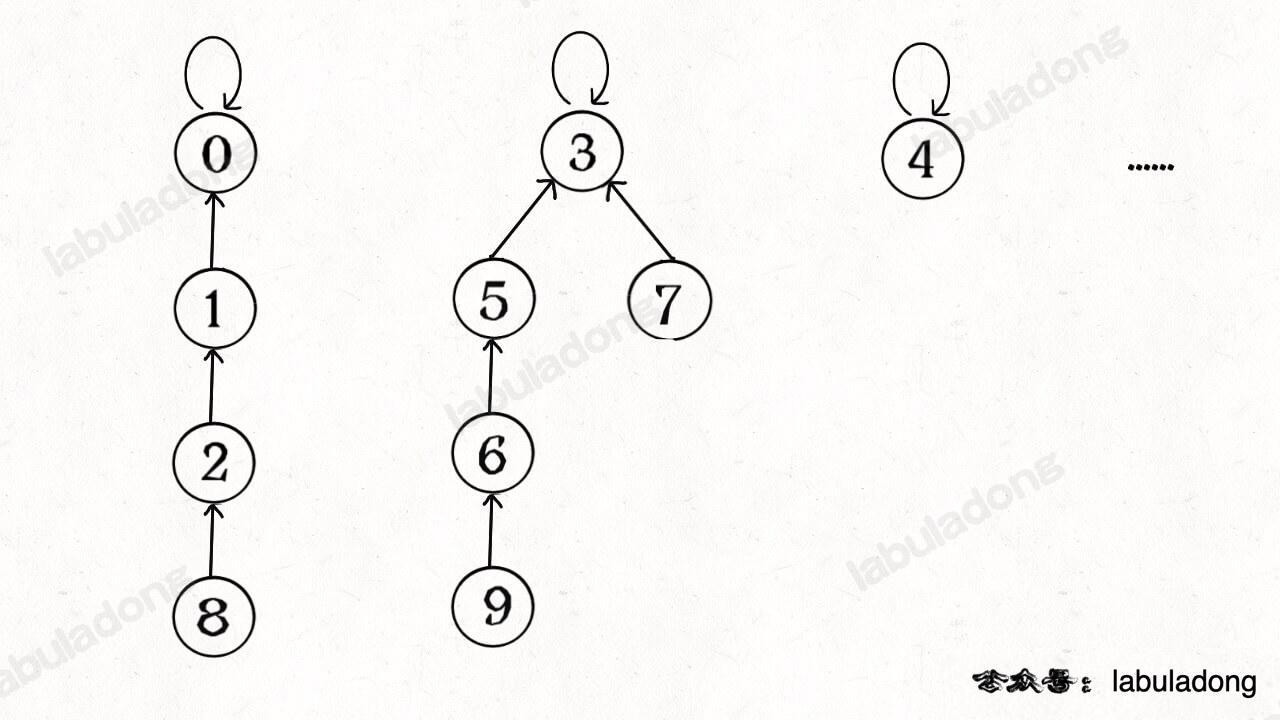
`find` 主要功能就是从某个节点向上遍历到树根,其时间复杂度就是树的高度。我们可能习惯性地认为树的高度就是 `logN`,但这并不一定。`logN` 的高度只存在于平衡二叉树,对于一般的树可能出现极端不平衡的情况,使得「树」几乎退化成「链表」,树的高度最坏情况下可能变成 `N`。
-
+
所以说上面这种解法,`find` , `union` , `connected` 的时间复杂度都是 O(N)。这个复杂度很不理想的,你想图论解决的都是诸如社交网络这样数据规模巨大的问题,对于 `union` 和 `connected` 的调用非常频繁,每次调用需要线性时间完全不可忍受。
@@ -179,7 +179,7 @@ public void union(int p, int q) {
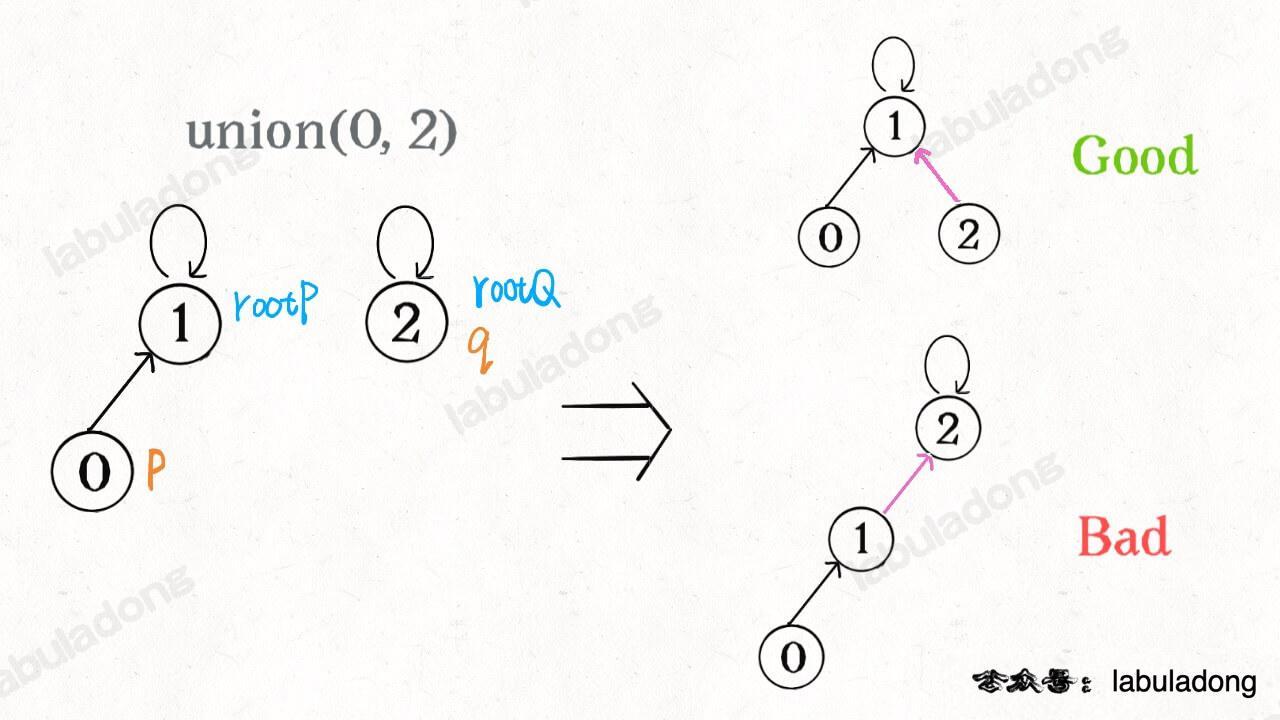
我们一开始就是简单粗暴的把 `p` 所在的树接到 `q` 所在的树的根节点下面,那么这里就可能出现「头重脚轻」的不平衡状况,比如下面这种局面:
-
+
长此以往,树可能生长得很不平衡。**我们其实是希望,小一些的树接到大一些的树下面,这样就能避免头重脚轻,更平衡一些**。解决方法是额外使用一个 `size` 数组,记录每棵树包含的节点数,我们不妨称为「重量」:
@@ -238,7 +238,7 @@ public void union(int p, int q) {
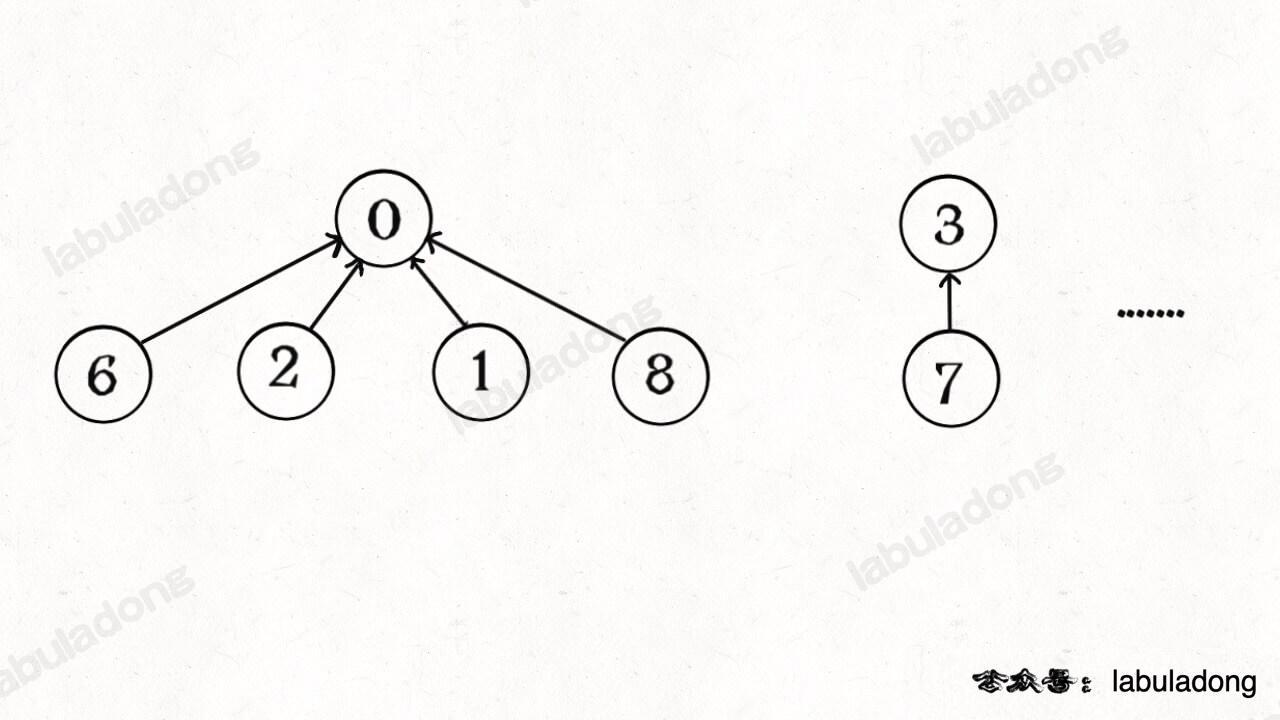
因为无论树长啥样,树上的每个节点的根节点都是相同的,所以能不能进一步压缩每棵树的高度,使树高始终保持为常数?
-
+
这样每个节点的父节点就是整棵树的根节点,`find` 就能以 O(1) 的时间找到某一节点的根节点,相应的,`connected` 和 `union` 复杂度都下降为 O(1)。
@@ -259,7 +259,7 @@ private int find(int x) {
这个操作有点匪夷所思,看个 GIF 就明白它的作用了(为清晰起见,这棵树比较极端):
-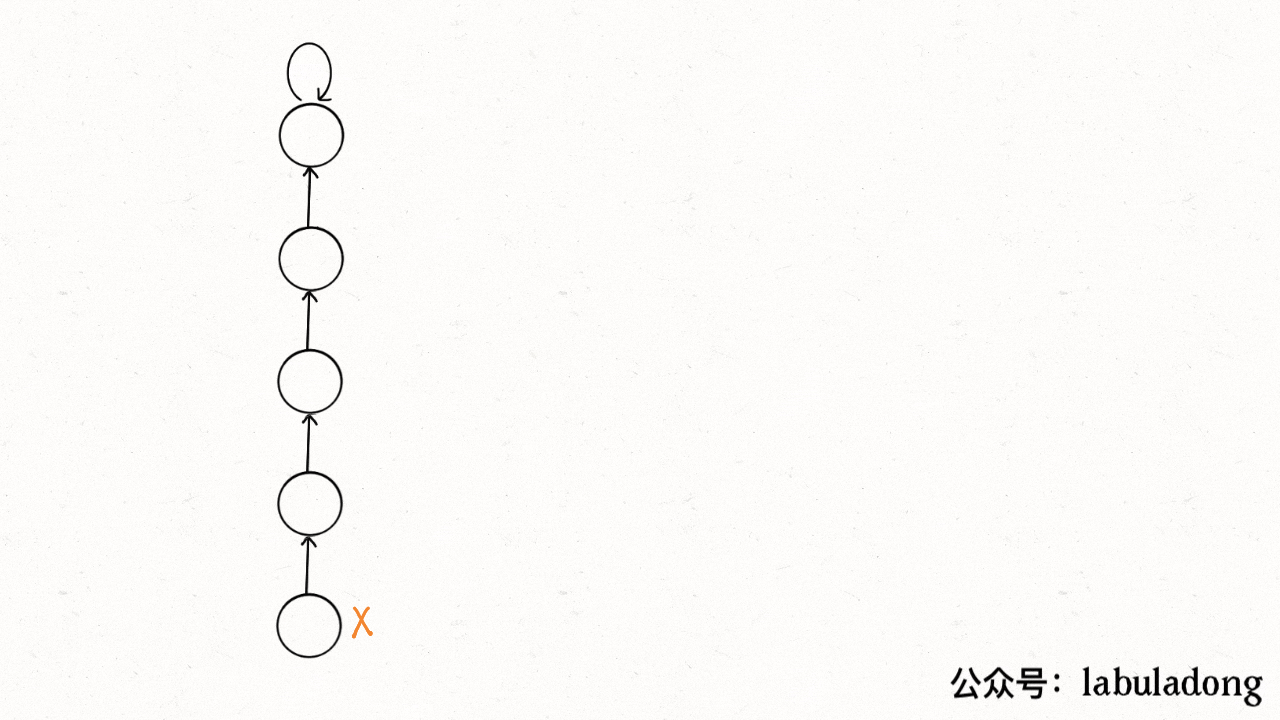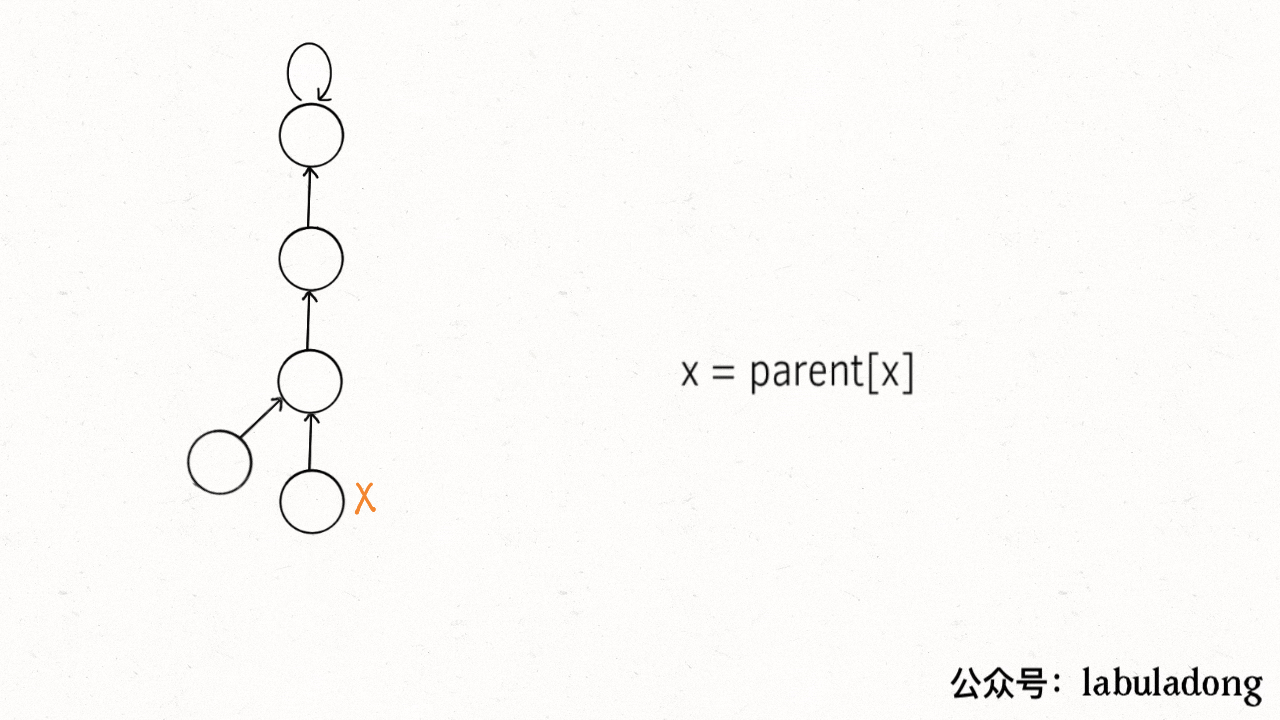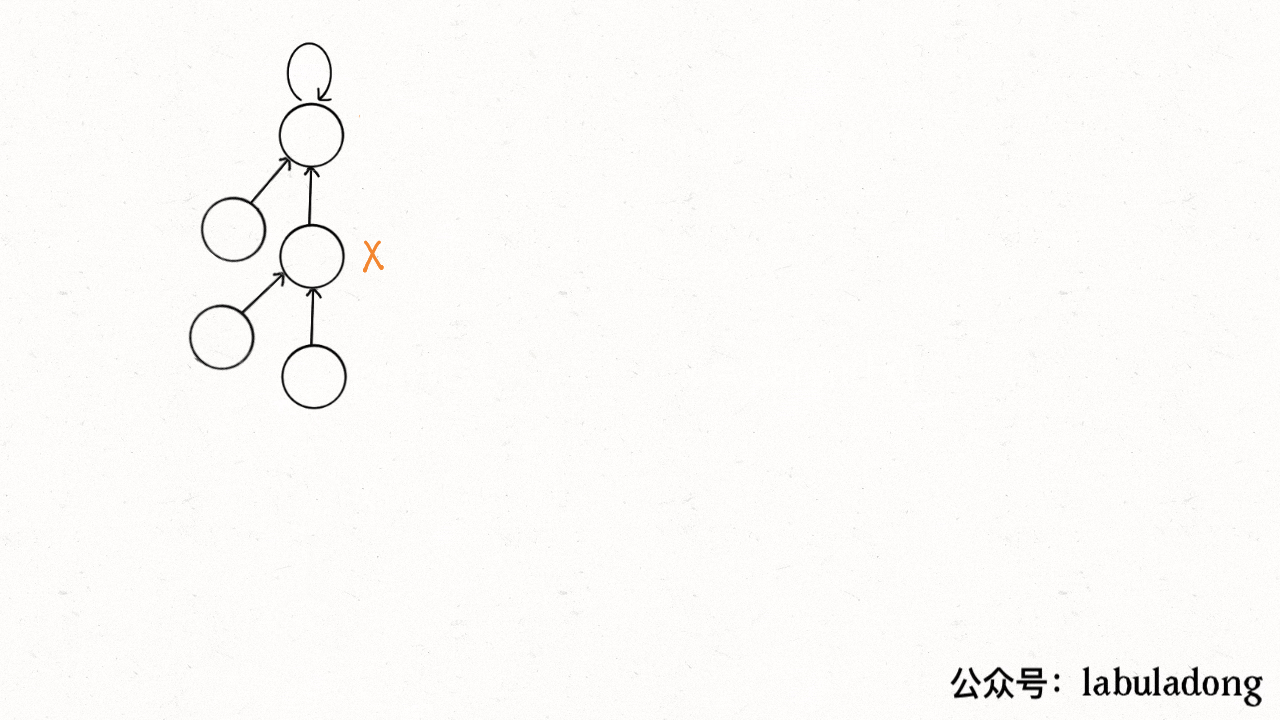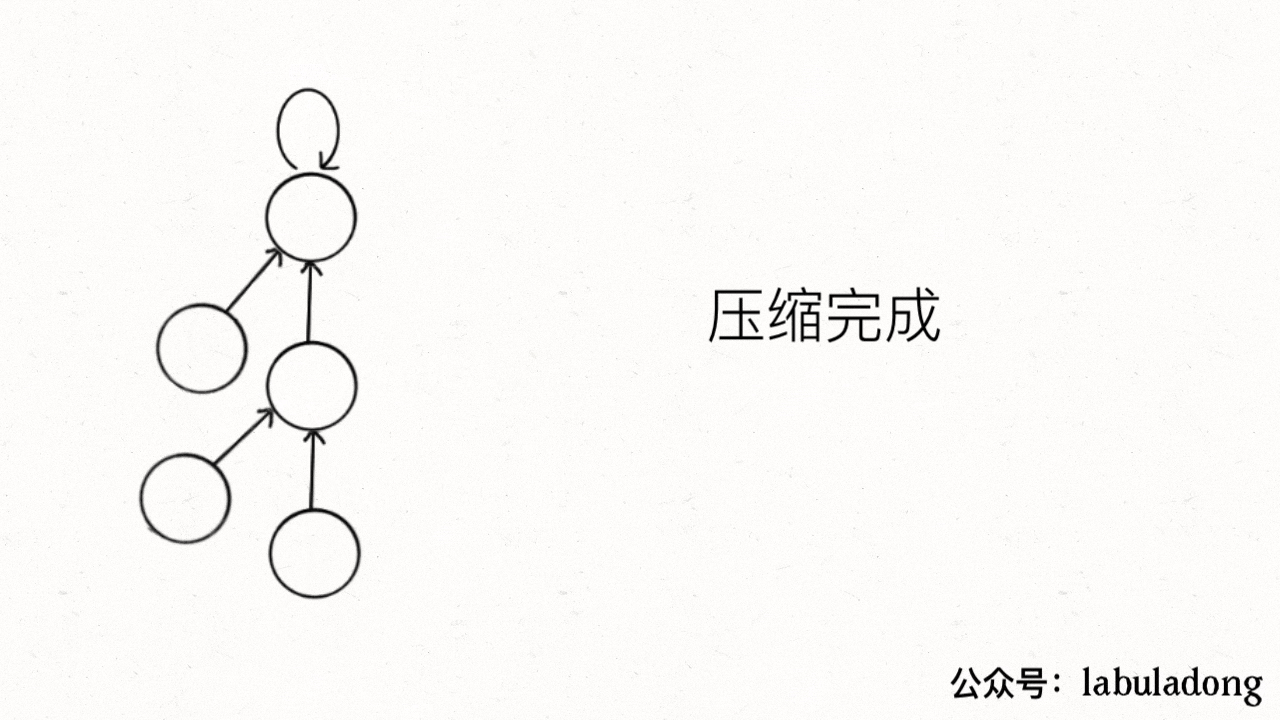
+
用语言描述就是,每次 while 循环都会把一对儿父子节点改到同一层,这样每次调用 `find` 函数向树根遍历的同时,顺手就将树高缩短了。
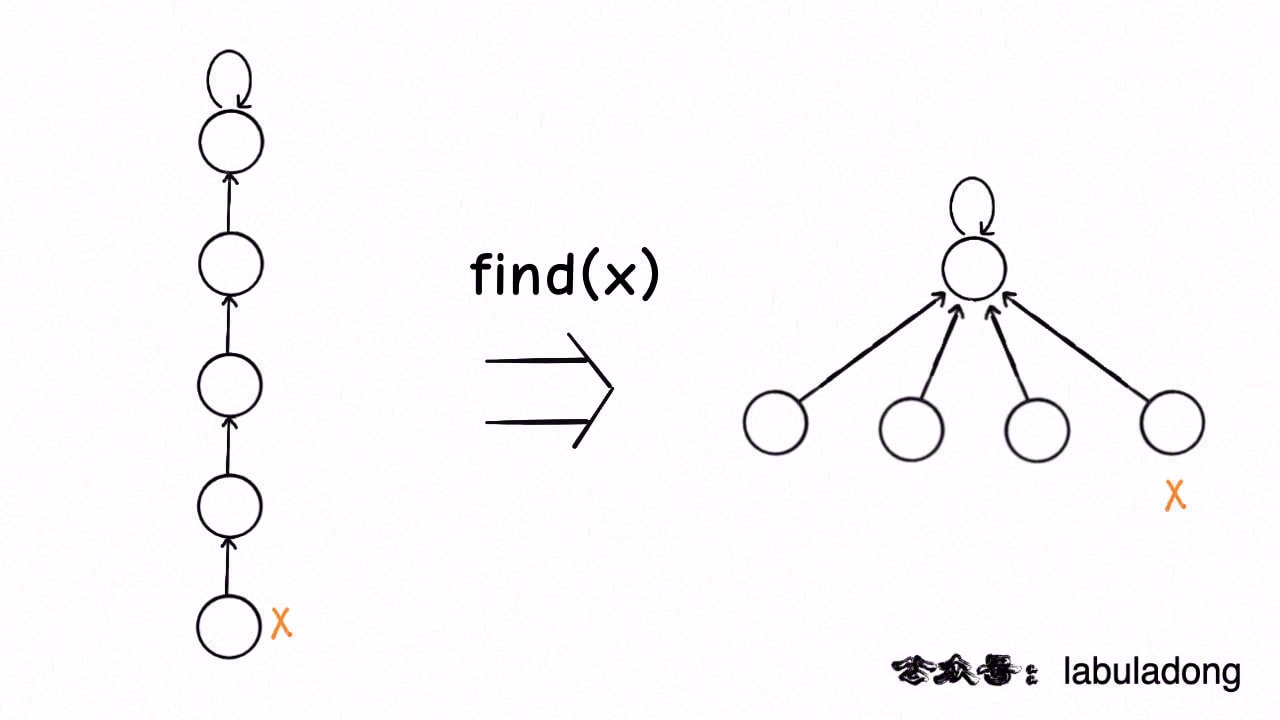
@@ -300,7 +300,7 @@ public int find(int x) {
这种路径压缩的效果如下:
-
+
比起第一种路径压缩,显然这种方法压缩得更彻底,直接把一整条树枝压平,一点意外都没有。就算一些极端情况下产生了一棵比较高的树,只要一次路径压缩就能大幅降低树高,从 [摊还分析](https://labuladong.github.io/article/fname.html?fname=时间复杂度) 的角度来看,所有操作的平均时间复杂度依然是 O(1),所以从效率的角度来说,推荐你使用这种路径压缩算法。
@@ -410,7 +410,7 @@ void solve(char[][] board);
注意哦,必须是四面被围的 `O` 才能被换成 `X`,也就是说边角上的 `O` 一定不会被围,进一步,与边角上的 `O` 相连的 `O` 也不会被 `X` 围四面,也不会被替换。
-
+
> PS:这让我想起小时候玩的棋类游戏「黑白棋」,只要你用两个棋子把对方的棋子夹在中间,对方的子就被替换成你的子。可见,占据四角的棋子是无敌的,与其相连的边棋子也是无敌的(无法被夹掉)。
@@ -422,7 +422,7 @@ void solve(char[][] board);
**你可以把那些不需要被替换的 `O` 看成一个拥有独门绝技的门派,它们有一个共同「祖师爷」叫 `dummy`,这些 `O` 和 `dummy` 互相连通,而那些需要被替换的 `O` 与 `dummy` 不连通**。
-
+
这就是 Union-Find 的核心思路,明白这个图,就很容易看懂代码了。
@@ -543,7 +543,7 @@ class UF {
- [一文秒杀所有岛屿题目](https://labuladong.github.io/article/fname.html?fname=岛屿题目)
- [二分图判定算法](https://labuladong.github.io/article/fname.html?fname=二分图)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
@@ -573,7 +573,7 @@ class UF {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円350円257円246円350円247円243円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円350円257円246円350円247円243円.md"
index 38bb7d6a93..c190c24856 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円350円257円246円350円247円243円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円350円257円246円350円247円243円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -37,7 +37,7 @@
你要是没有正确理解这些细节,写二分肯定就是玄学编程,有没有 bug 只能靠菩萨保佑(谁写谁知道)。我特意写了一首诗来歌颂该算法,概括本文的主要内容,建议保存(手动狗头):
-
+
本文就来探究几个最常用的二分查找场景:寻找一个数、寻找左侧边界、寻找右侧边界。而且,我们就是要深入细节,比如不等号是否应该带等号,`mid` 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因,保证你能灵活准确地写出正确的二分查找算法。
@@ -327,7 +327,7 @@ if (nums[mid] == target) {
// 这样想: mid = left - 1
```
-
+
因为我们对 `left` 的更新必须是 `left = mid + 1`,就是说 while 循环结束时,`nums[left]` 一定不等于 `target` 了,而 `nums[left-1]` 可能是 `target`。
@@ -518,7 +518,7 @@ int right_bound(int[] nums, int target) {
- [快速排序详解及应用](https://labuladong.github.io/article/fname.html?fname=快速排序)
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
- [讲两道常考的阶乘算法题](https://labuladong.github.io/article/fname.html?fname=阶乘题目)
@@ -558,7 +558,7 @@ int right_bound(int[] nums, int target) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円207円240円344円270円252円345円217円215円347円233円264円350円247円211円347円232円204円346円246円202円347円216円207円351円227円256円351円242円230円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円207円240円344円270円252円345円217円215円347円233円264円350円247円211円347円232円204円346円246円202円347円216円207円351円227円256円351円242円230円.md"
index 433e99238b..c9f903d9ae 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円207円240円344円270円252円345円217円215円347円233円264円350円247円211円347円232円204円346円246円202円347円216円207円351円227円256円351円242円230円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円207円240円344円270円252円345円217円215円347円233円264円350円247円211円347円232円204円346円246円202円347円216円207円351円227円256円351円242円230円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -83,7 +83,7 @@
那为什么只要 23 个人出现相同生日的概率就能大于 50% 了呢?我们先计算 23 个人生日都唯一(不重复)的概率。只有 1 个人的时候,生日唯一的概率是 `365/365`,2 个人时,生日唯一的概率是 `365/365 ×ばつ 364/365`,以此类推可知 23 人的生日都唯一的概率:
-
+
算出来大约是 0.493,所以存在相同生日的概率就是 0.507,差不多就是 50% 了。实际上,按照这个算法,当人数达到 70 时,存在两个人生日相同的概率就上升到了 99.9%,基本可以认为是 100% 了。所以从概率上说,一个几十人的小团体中存在生日相同的人真没啥稀奇的。
@@ -95,13 +95,13 @@
你是游戏参与者,现在有门 1,2,3,假设你随机选择了门 1,然后主持人打开了门 3 告诉你那后面是山羊。现在,你是坚持你最初的选择门 1,还是选择换成门 2 呢?
-
+
答案是应该换门,换门之后抽到跑车的概率是 2/3,不换的话是 1/3。又一次反直觉,感觉换不换的中奖概率应该都一样啊,因为最后肯定就剩两个门,一个是羊,一个是跑车,这是事实,所以不管选哪个的概率不都是 1/2 吗?
类似前面说的男孩女孩问题,最简单稳妥的方法就是把所有可能结果穷举出来:
-
+
很容易看到选择换门中奖的概率是 2/3,不换的话是 1/3。
@@ -135,7 +135,7 @@
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円211円215円347円274円200円345円222円214円346円212円200円345円267円247円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円211円215円347円274円200円345円222円214円346円212円200円345円267円247円.md"
index 10155987d4..26414cada7 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円211円215円347円274円200円345円222円214円346円212円200円345円267円247円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円211円215円347円274円200円345円222円214円346円212円200円345円267円247円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -31,7 +31,7 @@
先看一道例题,力扣第 303 题「区域和检索 - 数组不可变」,让你计算数组区间内元素的和,这是一道标准的前缀和问题:
-
+
题目要求你实现这样一个类:
@@ -96,7 +96,7 @@ class NumArray {
核心思路是我们 new 一个新的数组 `preSum` 出来,`preSum[i]` 记录 `nums[0..i-1]` 的累加和,看图 10 = 3 + 5 + 2:
-
+
看这个 `preSum` 数组,如果我想求索引区间 `[1, 4]` 内的所有元素之和,就可以通过 `preSum[5] - preSum[1]` 得出。
@@ -126,11 +126,11 @@ for (int i = 1; i < count.length; i++) 这是力扣第 304 题「二维区域和检索 - 矩阵不可变」,其实和上一题类似,上一题是让你计算子数组的元素之和,这道题让你计算二维矩阵中子矩阵的元素之和: - + 比如说输入的 `matrix` 如下图: - + 按照题目要求,矩阵左上角为坐标原点 `(0, 0)`,那么 `sumRegion([2,1,4,3])` 就是图中红色的子矩阵,你需要返回该子矩阵的元素和 8。 @@ -138,7 +138,7 @@ for (int i = 1; i < count.length; i++) 注意任意子矩阵的元素和可以转化成它周边几个大矩阵的元素和的运算: - + 而这四个大矩阵有一个共同的特点,就是左上角都是 `(0, 0)` 原点。 @@ -230,7 +230,7 @@ class NumMatrix { **《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**: - + ======其他语言代码====== diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円217円214円346円214円207円351円222円210円346円212円200円345円267円247円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円217円214円346円214円207円351円222円210円346円212円200円345円267円247円.md" index fcadd59d87..e07d4fc39f 100644 --- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円217円214円346円214円207円351円222円210円346円212円200円345円267円247円.md" +++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円217円214円346円214円207円351円222円210円346円212円200円345円267円247円.md" @@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -45,7 +45,7 @@
比如说看下力扣第 26 题「删除有序数组中的重复项」,让你在有序数组去重:
-
+
函数签名如下:
@@ -90,7 +90,7 @@ int removeDuplicates(int[] nums) {
算法执行的过程如下 GIF 图:
-
+
再简单扩展一下,看看力扣第 83 题「删除排序链表中的重复元素」,如果给你一个有序的单链表,如何去重呢?
@@ -118,7 +118,7 @@ ListNode deleteDuplicates(ListNode head) {
算法执行的过程请看下面这个 GIF:
-
+
这里可能有读者会问,链表中那些重复的元素并没有被删掉,就让这些节点在链表上挂着,合适吗?
@@ -130,7 +130,7 @@ ListNode deleteDuplicates(ListNode head) {
比如力扣第 27 题「移除元素」,看下题目:
-
+
函数签名如下:
@@ -249,7 +249,7 @@ int binarySearch(int[] nums, int target) {
看下力扣第 167 题「两数之和 II」:
-
+
只要数组有序,就应该想到双指针技巧。这道题的解法有点类似二分查找,通过调节 `left` 和 `right` 就可以调整 `sum` 的大小:
@@ -320,7 +320,7 @@ boolean isPalindrome(String s) {
这就是力扣第 5 题「最长回文子串」:
-
+
函数签名如下:
@@ -394,7 +394,7 @@ String longestPalindrome(String s) {
- [我写了首诗,把滑动窗口算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=滑动窗口技巧进阶)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- [扫描线技巧:安排会议室](https://labuladong.github.io/article/fname.html?fname=安排会议室)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
- [田忌赛马背后的算法决策](https://labuladong.github.io/article/fname.html?fname=田忌赛马)
- [算法时空复杂度分析实用指南](https://labuladong.github.io/article/fname.html?fname=时间复杂度)
- [算法笔试「骗分」套路](https://labuladong.github.io/article/fname.html?fname=刷题技巧)
@@ -430,7 +430,7 @@ String longestPalindrome(String s) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円233円236円346円272円257円347円256円227円346円263円225円350円257円246円350円247円243円344円277円256円350円256円242円347円211円210円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円233円236円346円272円257円347円256円227円346円263円225円350円257円246円350円247円243円344円277円256円350円256円242円347円211円210円.md"
index 7eb1126067..8e2db47dba 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円233円236円346円272円257円347円256円227円346円263円225円350円257円246円350円247円243円344円277円256円350円256円242円347円211円210円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円233円236円346円272円257円347円256円227円346円263円225円350円257円246円350円247円243円344円277円256円350円256円242円347円211円210円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
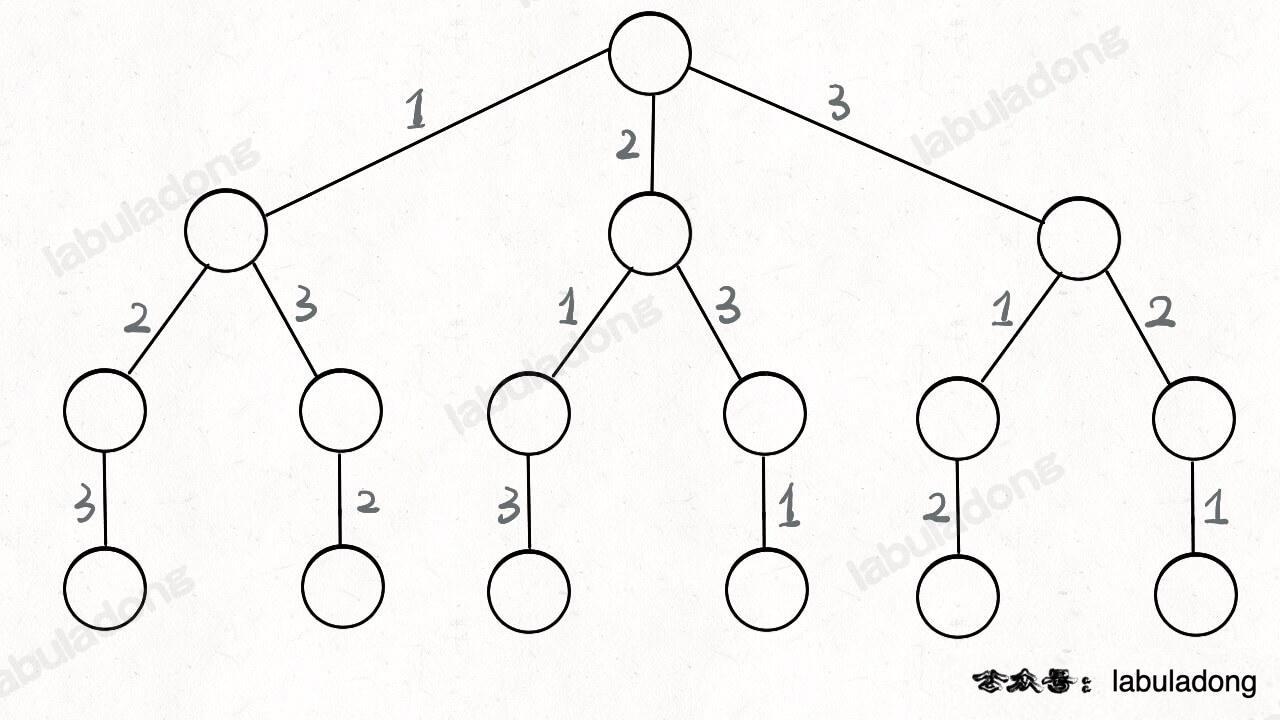
@@ -76,13 +76,13 @@ def backtrack(路径, 选择列表):
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
-
+
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。**我们不妨把这棵树称为回溯算法的「决策树」**。
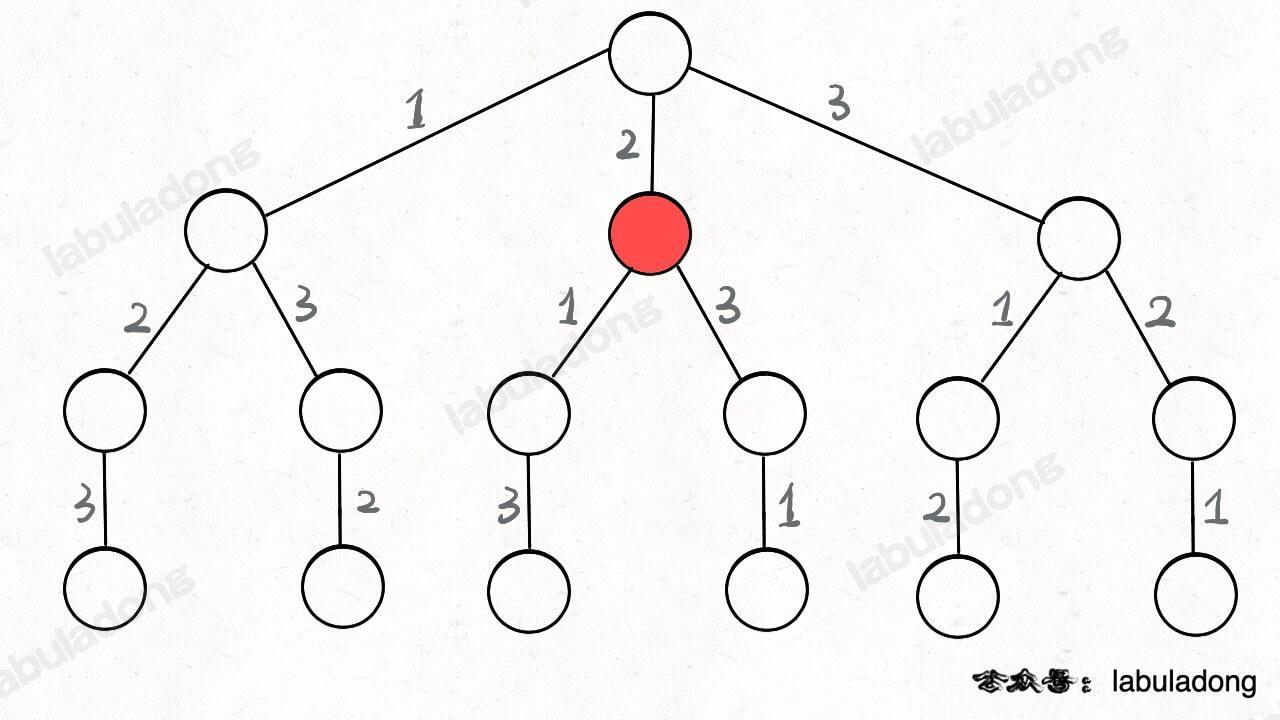
**为啥说这是决策树呢,因为你在每个节点上其实都在做决策**。比如说你站在下图的红色节点上:
-
+
你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
@@ -90,7 +90,7 @@ def backtrack(路径, 选择列表):
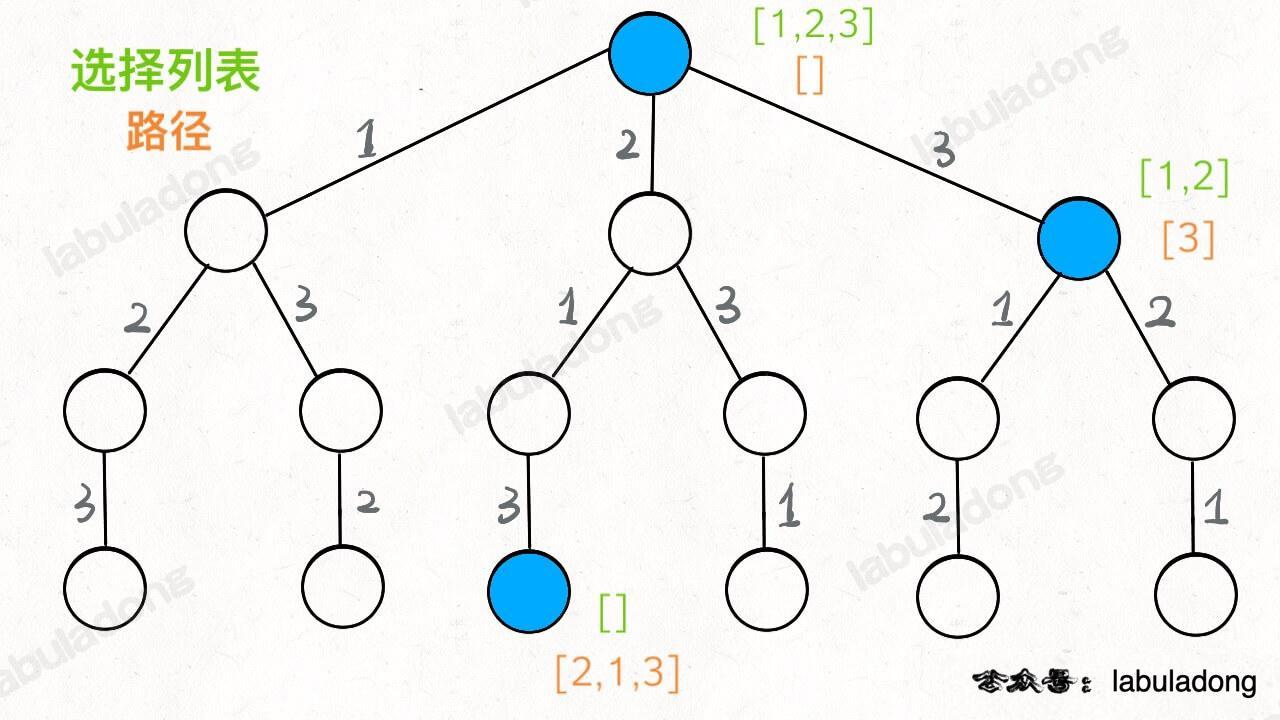
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个蓝色节点的属性:
-
+
**我们定义的 `backtrack` 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层叶子节点,其「路径」就是一个全排列**。
@@ -112,13 +112,13 @@ void traverse(TreeNode root) {
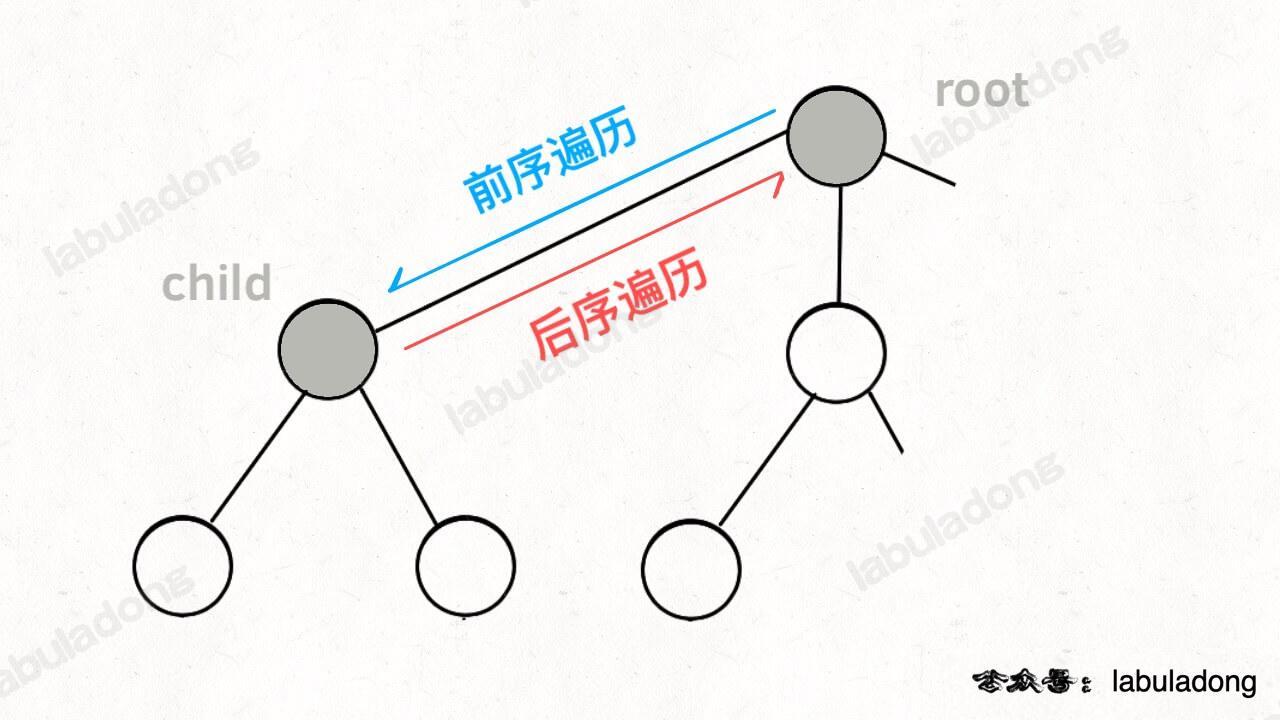
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:
-
+
**前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行**。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确处理节点的属性,那么就要在这两个特殊时间点搞点动作:
-
+
现在,你是否理解了回溯算法的这段核心框架?
@@ -181,7 +181,7 @@ void backtrack(int[] nums, LinkedList track, boolean[] used) {
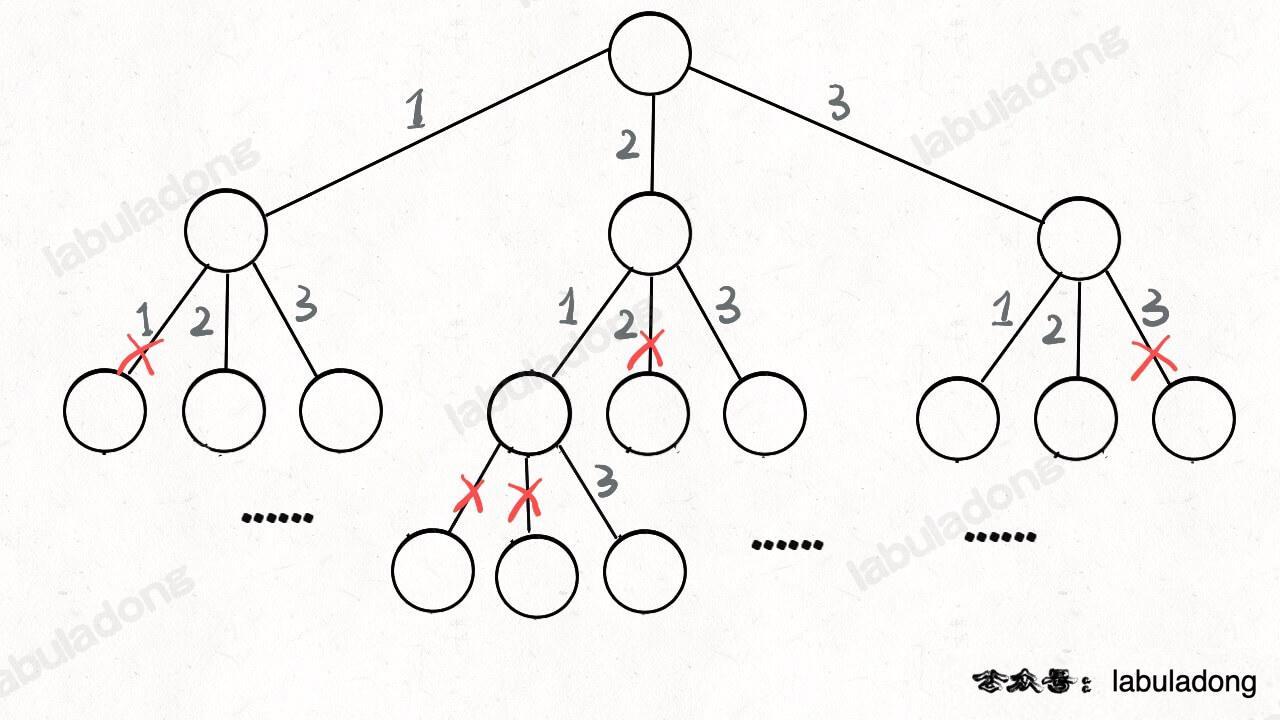
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 `used` 数组排除已经存在 `track` 中的元素,从而推导出当前的选择列表:
-
+
至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是最高效的,你可能看到有的解法连 `used` 数组都不使用,通过交换元素达到目的。但是那种解法稍微难理解一些,这里就不写了,有兴趣可以自行搜索一下。
@@ -270,7 +270,7 @@ bool isValid(vector& board, int row, int col) {
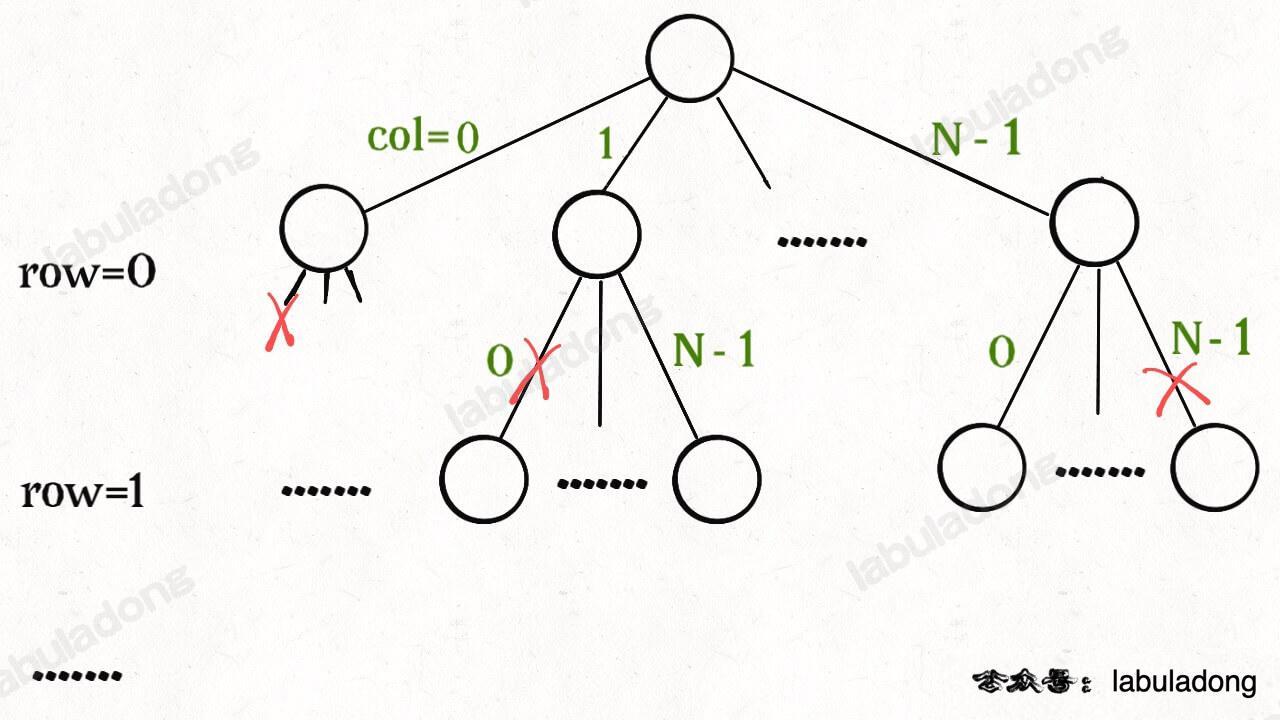
函数 `backtrack` 依然像个在决策树上游走的指针,通过 `row` 和 `col` 就可以表示函数遍历到的位置,通过 `isValid` 函数可以将不符合条件的情况剪枝:
-
+
如果直接给你这么一大段解法代码,可能是懵逼的。但是现在明白了回溯算法的框架套路,还有啥难理解的呢?无非是改改做选择的方式,排除不合法选择的方式而已,只要框架存于心,你面对的只剩下小问题了。
@@ -394,7 +394,7 @@ def backtrack(...):
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円227円347円254円246円344円270円262円344円271円230円346円263円225円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円227円347円254円246円344円270円262円344円271円230円346円263円225円.md"
index d5dce4e765..bda46d3eaf 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円227円347円254円246円344円270円262円344円271円230円346円263円225円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円227円347円254円246円344円270円262円344円271円230円346円263円225円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -25,13 +25,13 @@
看下力扣第 43 题「字符串相乘」:
-
+
需要注意的是,`num1` 和 `num2` 可以非常长,所以不可以把他们直接转成整型然后运算,唯一的思路就是模仿我们手算乘法。
比如说我们手算 `123 ×ばつ 45`,应该会这样计算:
-
+
计算 `123 ×ばつ 5`,再计算 `123 ×ばつ 4`,最后错一位相加。这个流程恐怕小学生都可以熟练完成,但是你是否能**把这个运算过程进一步机械化**,写成一套算法指令让没有任何智商的计算机来执行呢?
@@ -39,21 +39,21 @@
首先,我们这种手算方式还是太「高级」了,我们要再「低级」一点,`123 ×ばつ 5` 和 `123 ×ばつ 4` 的过程还可以进一步分解,最后再相加:
-
+
现在 `123` 并不大,如果是个很大的数字的话,是无法直接计算乘积的。我们可以用一个数组在底下接收相加结果:
-
+
整个计算过程大概是这样,**有两个指针 `i,j` 在 `num1` 和 `num2` 上游走,计算乘积,同时将乘积叠加到 `res` 的正确位置**,如下 GIF 图所示:
-
+
现在还有一个关键问题,如何将乘积叠加到 `res` 的正确位置,或者说,如何通过 `i,j` 计算 `res` 的对应索引呢?
其实,细心观察之后就发现,**`num1[i]` 和 `num2[j]` 的乘积对应的就是 `res[i+j]` 和 `res[i+j+1]` 这两个位置**。
-
+
明白了这一点,就可以用代码模仿出这个计算过程了:
@@ -102,7 +102,7 @@ string multiply(string num1, string num2) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円246円344円271円240円346円225円260円346円215円256円347円273円223円346円236円204円345円222円214円347円256円227円346円263円225円347円232円204円351円253円230円346円225円210円346円226円271円346円263円225円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円246円344円271円240円346円225円260円346円215円256円347円273円223円346円236円204円345円222円214円347円256円227円346円263円225円347円232円204円351円253円230円346円225円210円346円226円271円346円263円225円.md"
index c014cc20cc..337758f3f4 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円246円344円271円240円346円225円260円346円215円256円347円273円223円346円236円204円345円222円214円347円256円227円346円263円225円347円232円204円351円253円230円346円225円210円346円226円271円346円263円225円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円255円246円344円271円240円346円225円260円346円215円256円347円273円223円346円236円204円345円222円214円347円256円227円346円263円225円347円232円204円351円253円230円346円225円210円346円226円271円346円263円225円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -138,7 +138,7 @@ void traverse(TreeNode root) {
这是我这刷题多年的亲身体会,下图是我刚开始学算法的提交截图:
-
+
公众号文章的阅读数据显示,大部分人对数据结构相关的算法文章不感兴趣,而是更关心动规回溯分治等等技巧。为什么要先刷二叉树呢,**因为二叉树是最容易培养框架思维的,而且大部分算法技巧,本质上都是树的遍历问题**。
@@ -238,7 +238,7 @@ PS:[刷题插件](https://mp.weixin.qq.com/s/OE1zPVPj0V2o82N4HtLQbw) 集成了
[动态规划详解](https://labuladong.github.io/article/fname.html?fname=动态规划详解进阶)说过凑零钱问题,暴力解法就是遍历一棵 N 叉树:
-
+
```java
int dp(int[] coins, int amount) {
@@ -275,7 +275,7 @@ int dp(int amount) {
比如全排列问题吧,本质上全排列就是在遍历下面这棵树,到叶子节点的路径就是一个全排列:
-
+
全排列算法的主要代码如下:
@@ -384,7 +384,7 @@ N 叉树的遍历框架,找出来了吧?你说,树这种结构重不重要
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
\ No newline at end of file
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円267円256円345円210円206円346円212円200円345円267円247円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円267円256円345円210円206円346円212円200円345円267円247円.md"
index 98628bdea8..1214b55556 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円267円256円345円210円206円346円212円200円345円267円247円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円267円256円345円210円206円346円212円200円345円267円247円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -48,7 +48,7 @@ class PrefixSum {
}
```
-
+
`prefix[i]` 就代表着 `nums[0..i-1]` 所有元素的累加和,如果我们想求区间 `nums[i..j]` 的累加和,只要计算 `prefix[j+1] - prefix[i]` 即可,而不需要遍历整个区间求和。
@@ -71,7 +71,7 @@ for (int i = 1; i < nums.length; i++) { } ``` - + 通过这个 `diff` 差分数组是可以反推出原始数组 `nums` 的,代码逻辑如下: @@ -86,7 +86,7 @@ for (int i = 1; i < diff.length; i++) { **这样构造差分数组 `diff`,就可以快速进行区间增减的操作**,如果你想对区间 `nums[i..j]` 的元素全部加 3,那么只需要让 `diff[i] += 3`,然后再让 `diff[j+1] -= 3` 即可: -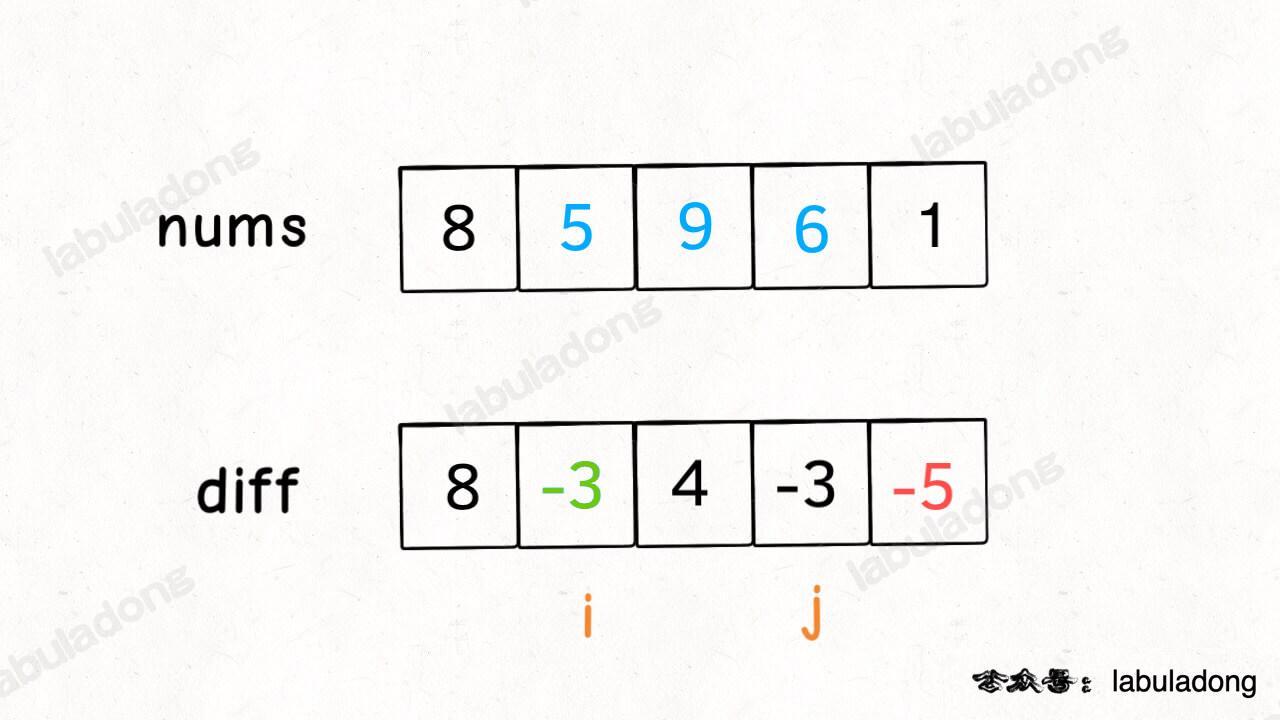 + **原理很简单,回想 `diff` 数组反推 `nums` 数组的过程,`diff[i] += 3` 意味着给 `nums[i..]` 所有的元素都加了 3,然后 `diff[j+1] -= 3` 又意味着对于 `nums[j+1..]` 所有元素再减 3,那综合起来,是不是就是对 `nums[i..j]` 中的所有元素都加 3 了**? @@ -150,7 +150,7 @@ public void increment(int i, int j, int val) { 首先,力扣第 370 题「区间加法」 就直接考察了差分数组技巧: - + 那么我们直接复用刚才实现的 `Difference` 类就能把这道题解决掉: @@ -174,7 +174,7 @@ int[] getModifiedArray(int length, int[][] updates) { 当然,实际的算法题可能需要我们对题目进行联想和抽象,不会这么直接地让你看出来要用差分数组技巧,这里看一下力扣第 1109 题「航班预订统计」: - + 函数签名如下: @@ -297,4 +297,4 @@ boolean carPooling(int[][] trips, int capacity) { **《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**: - \ No newline at end of file + \ No newline at end of file diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円270円270円347円224円250円347円232円204円344円275円215円346円223円215円344円275円234円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円270円270円347円224円250円347円232円204円344円275円215円346円223円215円344円275円234円.md" index 41c0d54b60..4ae00672aa 100644 --- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円270円270円347円224円250円347円232円204円344円275円215円346円223円215円344円275円234円.md" +++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/345円270円270円347円224円250円347円232円204円344円275円215円346円223円215円344円275円234円.md" @@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -100,7 +100,7 @@ n = ~-n;
看个图就很容易理解了:
-
+
其核心逻辑就是,`n - 1` 一定可以消除最后一个 1,同时把其后的 0 都变成 1,这样再和 `n` 做一次 `&` 运算,就可以仅仅把最后一个 1 变成 0 了。
@@ -108,7 +108,7 @@ n = ~-n;
这是力扣第 191 题「位 1 的个数」:
-
+
就是让你返回 `n` 的二进制表示中有几个 1。因为 `n & (n - 1)` 可以消除最后一个 1,所以可以用一个循环不停地消除 1 同时计数,直到 `n` 变成 0 为止。
@@ -154,7 +154,7 @@ boolean isPowerOfTwo(int n) {
这是力扣第 136 题「只出现一次的数字」:
-
+
对于这道题目,我们只要把所有数字进行异或,成对儿的数字就会变成 0,落单的数字和 0 做异或还是它本身,所以最后异或的结果就是只出现一次的元素:
@@ -172,7 +172,7 @@ int singleNumber(int[] nums) {
这是力扣第 268 题「丢失的数字」:
-
+
给一个长度为 `n` 的数组,其索引应该在 `[0,n)`,但是现在你要装进去 `n + 1` 个元素 `[0,n]`,那么肯定有一个元素装不下嘛,请你找出这个缺失的元素。
@@ -212,11 +212,11 @@ int missingNumber(int[] nums) {
而这道题索就可以通过这些性质巧妙算出缺失的那个元素,比如说 `nums = [0,3,1,4]`:
-
+
为了容易理解,我们假设先把索引补一位,然后让每个元素和自己相等的索引相对应:
-
+
这样做了之后,就可以发现除了缺失元素之外,所有的索引和元素都组成一对儿了,现在如果把这个落单的索引 2 找出来,也就找到了缺失的那个元素。
@@ -235,7 +235,7 @@ int missingNumber(int[] nums) {
}
```
-
+
由于异或运算满足交换律和结合律,所以总是能把成对儿的数字消去,留下缺失的那个元素。
@@ -276,7 +276,7 @@ http://graphics.stanford.edu/~seander/bithacks.html#ReverseParallel
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円264円227円347円211円214円347円256円227円346円263円225円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円264円227円347円211円214円347円256円227円346円263円225円.md"
index 903246b670..0b89130d23 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円264円227円347円211円214円347円256円227円346円263円225円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円264円227円347円211円214円347円256円227円346円263円225円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -84,15 +84,15 @@ void shuffle(int[] arr) {
for 循环第一轮迭代时,`i = 0`,`rand` 的取值范围是 `[0, 4]`,有 5 个可能的取值。
-
+
for 循环第二轮迭代时,`i = 1`,`rand` 的取值范围是 `[1, 4]`,有 4 个可能的取值。
-
+
后面以此类推,直到最后一次迭代,`i = 4`,`rand` 的取值范围是 `[4, 4]`,只有 1 个可能的取值。
-
+
可以看到,整个过程产生的所有可能结果有 `n! = 5! = 5*4*3*2*1` 种,所以这个算法是正确的。
@@ -137,7 +137,7 @@ void shuffle(int[] arr) {
记得高中有道数学题:往一个正方形里面随机打点,这个正方形里紧贴着一个圆,告诉你打点的总数和落在圆里的点的数量,让你计算圆周率。
-
+
这其实就是利用了蒙特卡罗方法:当打的点足够多的时候,点的数量就可以近似代表图形的面积。通过面积公式,由正方形和圆的面积比值是可以很容易推出圆周率的。当然打的点越多,算出的圆周率越准确,充分体现了大力出奇迹的真理。
@@ -145,7 +145,7 @@ void shuffle(int[] arr) {
**第一种思路**,我们把数组 arr 的所有排列组合都列举出来,做成一个直方图(假设 arr = {1,2,3}):
-
+
每次进行洗牌算法后,就把得到的打乱结果对应的频数加一,重复进行 100 万次,如果每种结果出现的总次数差不多,那就说明每种结果出现的概率应该是相等的。写一下这个思路的伪代码:
@@ -190,7 +190,7 @@ for (int feq : count)
print(feq / N + " "); // 频率
```
-
+
这种思路也是可行的,而且避免了阶乘级的空间复杂度,但是多了嵌套 for 循环,时间复杂度高一点。不过由于我们的测试数据量不会有多大,这些问题都可以忽略。
@@ -210,7 +210,7 @@ for (int feq : count)
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円273円221円345円212円250円347円252円227円345円217円243円346円212円200円345円267円247円350円277円233円351円230円266円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円273円221円345円212円250円347円252円227円345円217円243円346円212円200円345円267円247円350円277円233円351円230円266円.md"
index 0a7096140a..235f752521 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円273円221円345円212円250円347円252円227円345円217円243円346円212円200円345円267円247円350円277円233円351円230円266円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/346円273円221円345円212円250円347円252円227円345円217円243円346円212円200円345円267円247円350円277円233円351円230円266円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -33,7 +33,7 @@
鉴于前文 [二分搜索框架详解](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 的那首《二分搜索升天词》很受好评,并在民间广为流传,成为安睡助眠的一剂良方,今天在滑动窗口算法框架中,我再次编写一首小诗来歌颂滑动窗口算法的伟大(手动狗头):
-
+
哈哈,我自己快把自己夸上天了,大家乐一乐就好,不要当真:)
@@ -124,7 +124,7 @@ void slidingWindow(string s) {
先来看看力扣第 76 题「最小覆盖子串」难度 Hard:
-
+
就是说要在 `S`(source) 中找到包含 `T`(target) 中全部字母的一个子串,且这个子串一定是所有可能子串中最短的。
@@ -157,19 +157,19 @@ for (int i = 0; i < s.size(); i++) 初始状态: -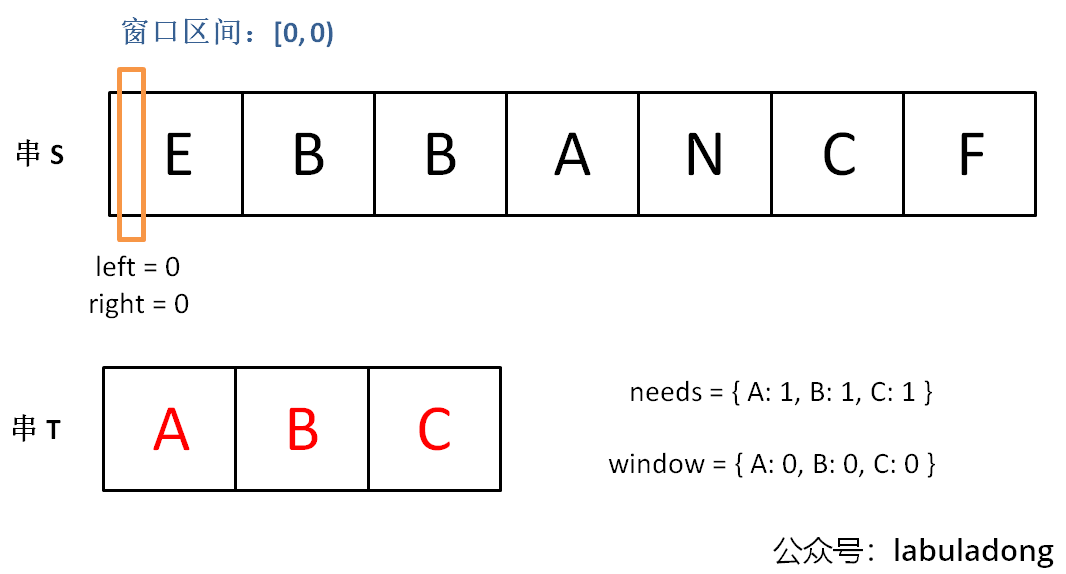 + 增加 `right`,直到窗口 `[left, right)` 包含了 `T` 中所有字符: -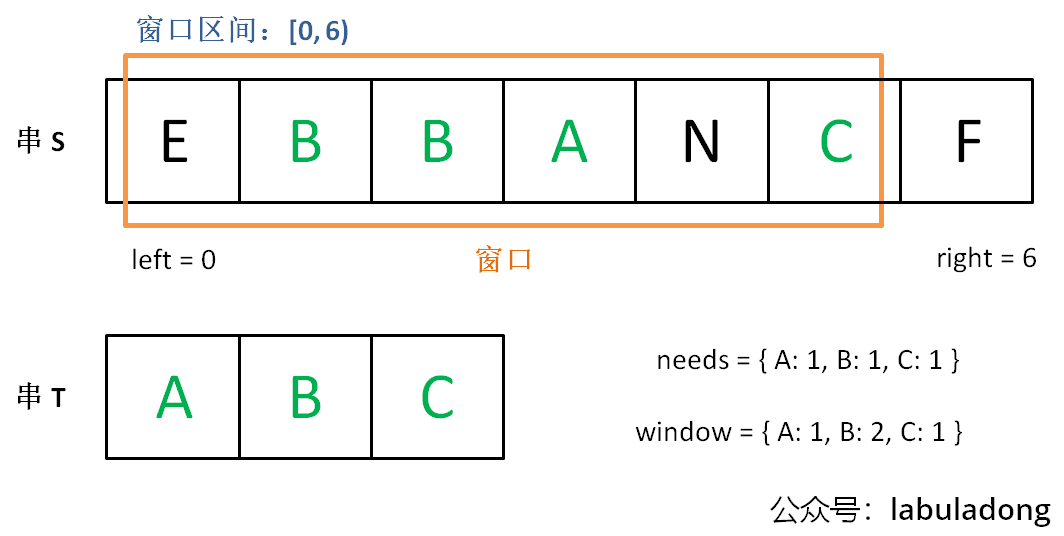 + 现在开始增加 `left`,缩小窗口 `[left, right)`: -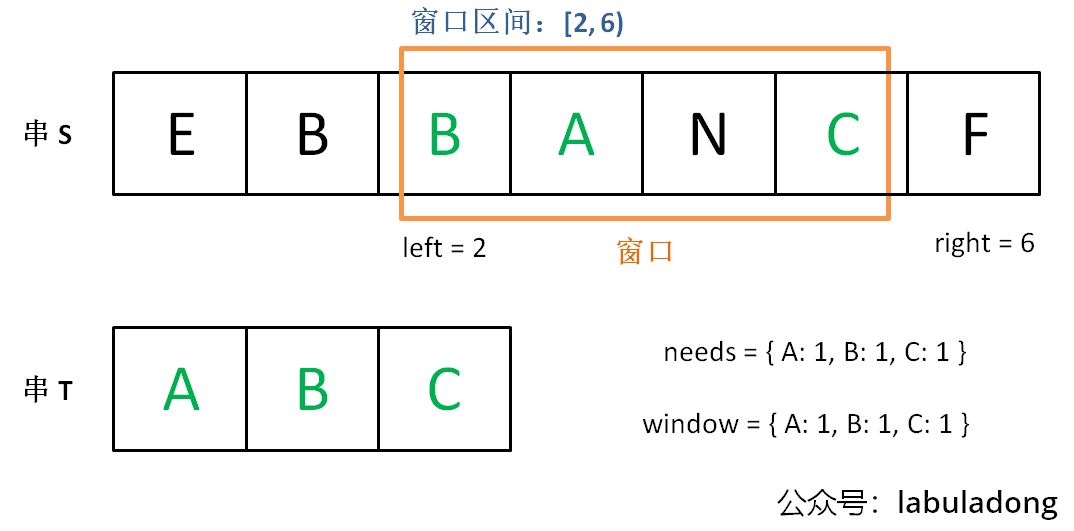 + 直到窗口中的字符串不再符合要求,`left` 不再继续移动: -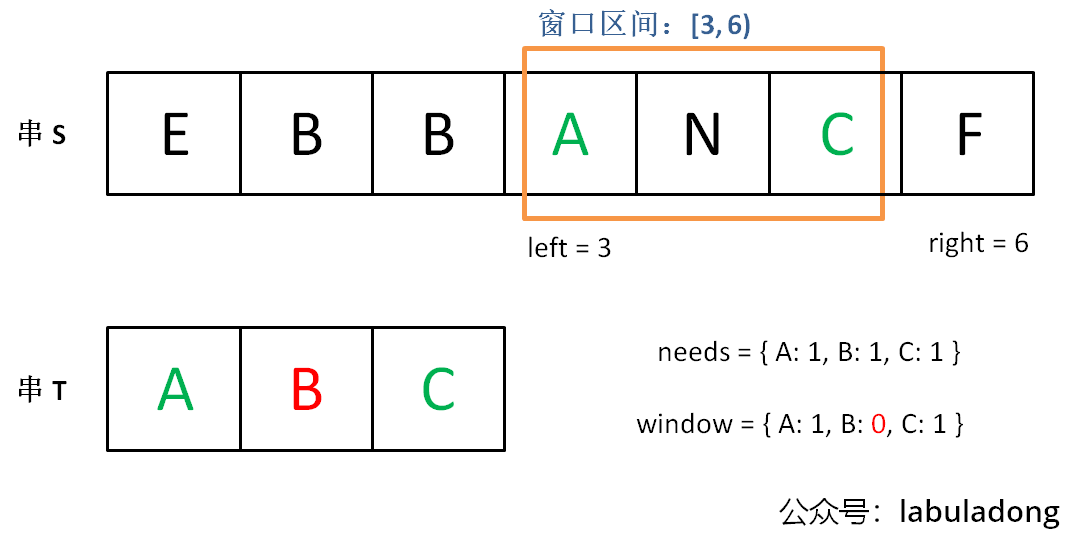 + 之后重复上述过程,先移动 `right`,再移动 `left`...... 直到 `right` 指针到达字符串 `S` 的末端,算法结束。 @@ -268,7 +268,7 @@ string minWindow(string s, string t) { 这是力扣第 567 题「字符串的排列」,难度中等: - + 注意哦,输入的 `s1` 是可以包含重复字符的,所以这个题难度不小。 @@ -328,7 +328,7 @@ bool checkInclusion(string t, string s) { 这是力扣第 438 题「找到字符串中所有字母异位词」,难度中等: - + 呵呵,这个所谓的字母异位词,不就是排列吗,搞个高端的说法就能糊弄人了吗?**相当于,输入一个串 `S`,一个串 `T`,找到 `S` 中所有 `T` 的排列,返回它们的起始索引**。 @@ -376,7 +376,7 @@ vector findAnagrams(string s, string t) {
这是力扣第 3 题「无重复字符的最长子串」,难度中等:
-
+
这个题终于有了点新意,不是一套框架就出答案,不过反而更简单了,稍微改一改框架就行了:
@@ -480,4 +480,4 @@ int lengthOfLongestSubstring(string s) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/347円203円247円351円245円274円346円216円222円345円272円217円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/347円203円247円351円245円274円346円216円222円345円272円217円.md"
index c408552e3d..c72bd17cf8 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/347円203円247円351円245円274円346円216円222円345円272円217円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/347円203円247円351円245円274円346円216円222円345円272円217円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -23,17 +23,17 @@
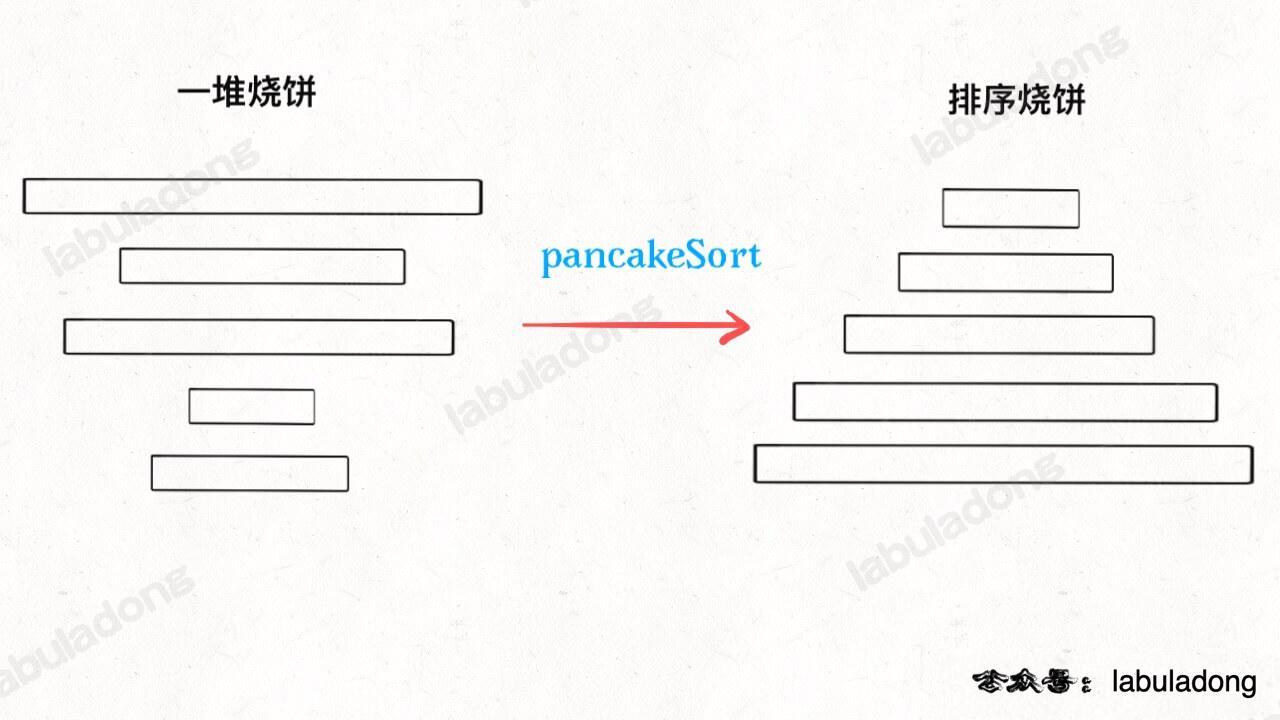
力扣第 969 题「煎饼排序」是个很有意思的实际问题:假设盘子上有 `n` 块**面积大小不一**的烧饼,你如何用一把锅铲进行若干次翻转,让这些烧饼的大小有序(小的在上,大的在下)?
-
+
设想一下用锅铲翻转一堆烧饼的情景,其实是有一点限制的,我们每次只能将最上面的若干块饼子翻转:
-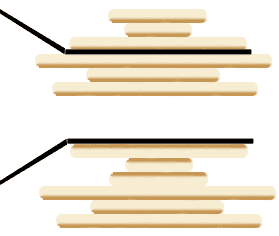
+
我们的问题是,**如何使用算法得到一个翻转序列,使得烧饼堆变得有序**?
首先,需要把这个问题抽象,用数组来表示烧饼堆:
-
+
如何解决这个问题呢?其实类似上篇文章 [递归反转链表的一部分](https://labuladong.github.io/article/fname.html?fname=递归反转链表的一部分),这也是需要**递归思想**的。
@@ -48,11 +48,11 @@ void sort(int[] cakes, int n);
如果我们找到了前 `n` 个烧饼中最大的那个,然后设法将这个饼子翻转到最底下:
-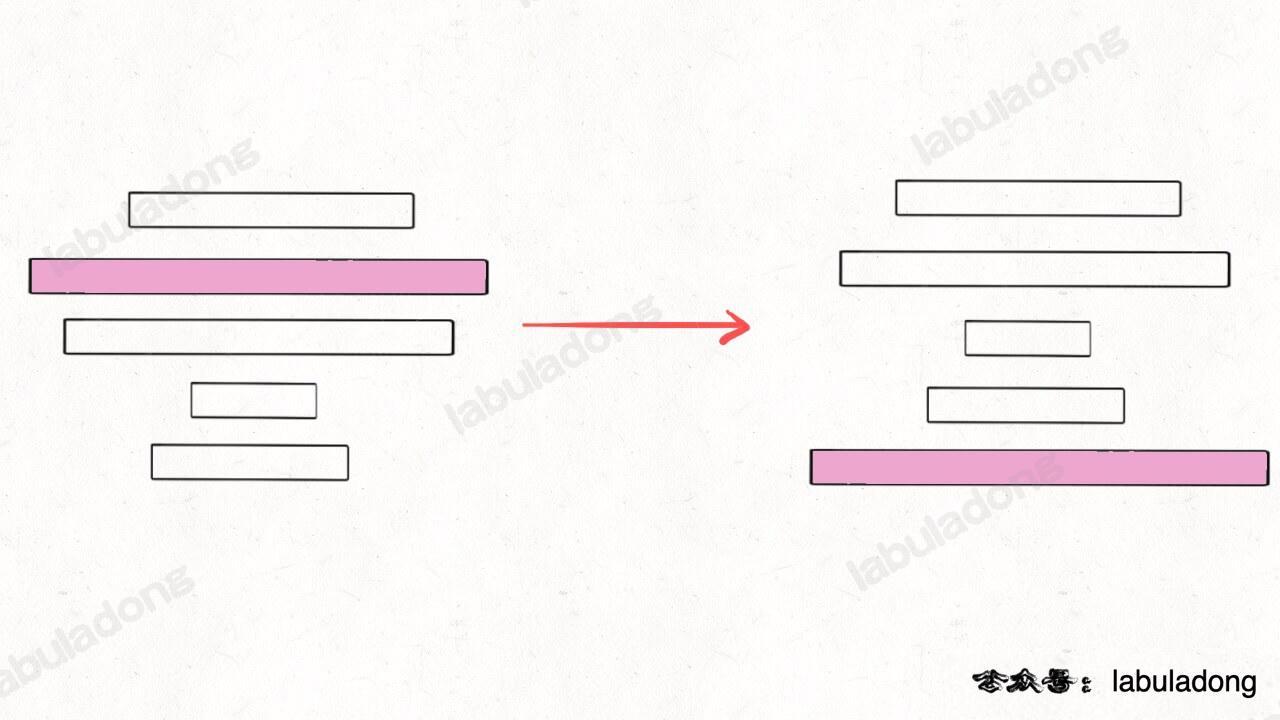
+
那么,原问题的规模就可以减小,递归调用 `pancakeSort(A, n-1)` 即可:
-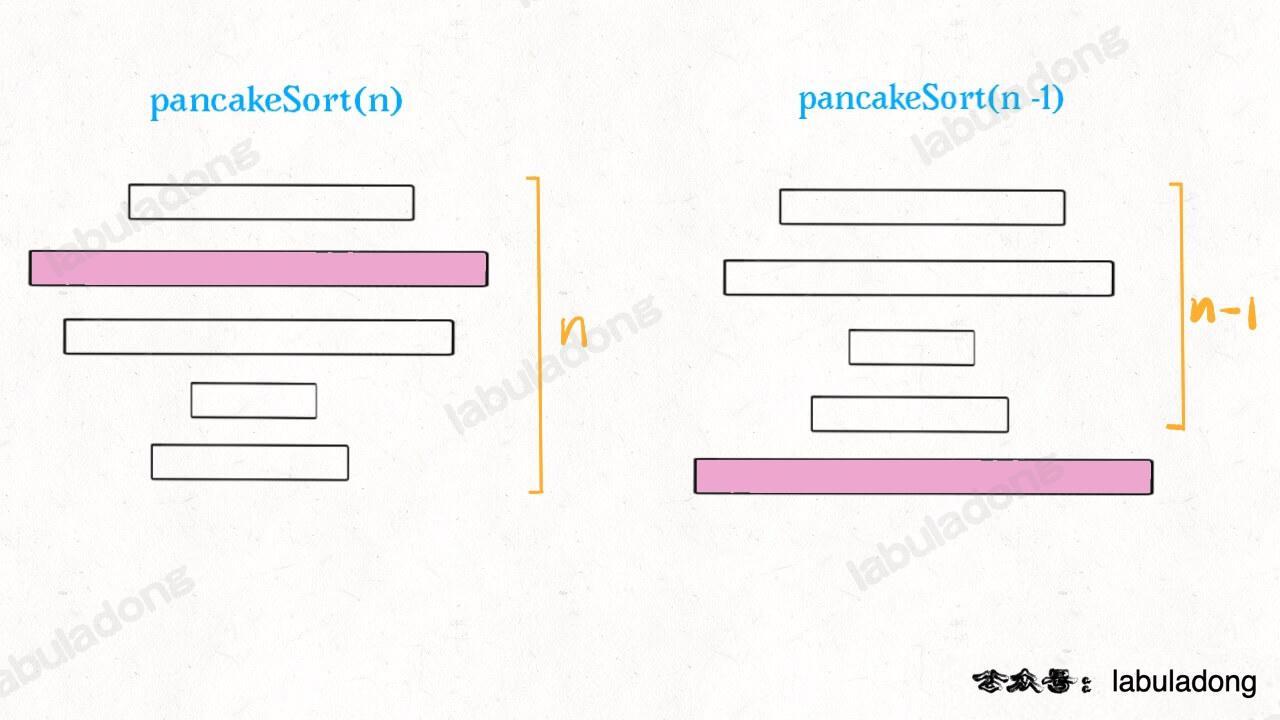
+
接下来,对于上面的这 `n - 1` 块饼,如何排序呢?还是先从中找到最大的一块饼,然后把这块饼放到底下,再递归调用 `pancakeSort(A, n-1-1)`......
@@ -150,7 +150,7 @@ void reverse(int[] arr, int i, int j) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/350円212円261円345円274円217円351円201円215円345円216円206円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/350円212円261円345円274円217円351円201円215円345円216円206円.md"
index ae476ef69a..2d4f8bfbe4 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/350円212円261円345円274円217円351円201円215円345円216円206円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/350円212円261円345円274円217円351円201円215円345円216円206円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
对二维数组进行旋转是常见的笔试题,力扣第 48 题「旋转图像」就是很经典的一道:
-
+
题目很好理解,就是让你将一个二维矩阵顺时针旋转 90 度,**难点在于要「原地」修改**,函数签名如下:
@@ -45,7 +45,7 @@ void rotate(int[][] matrix)
如何「原地」旋转二维矩阵?稍想一下,感觉操作起来非常复杂,可能要设置巧妙的算法机制来「一圈一圈」旋转矩阵:
-
+
**但实际上,这道题不能走寻常路**,在讲巧妙解法之前,我们先看另一道谷歌曾经考过的算法题热热身:
@@ -87,15 +87,15 @@ s = "labuladong world hello"
**我们可以先将 `n x n` 矩阵 `matrix` 按照左上到右下的对角线进行镜像对称**:
-
+
**然后再对矩阵的每一行进行反转**:
-
+
**发现结果就是 `matrix` 顺时针旋转 90 度的结果**:
-
+
将上述思路翻译成代码,即可解决本题:
@@ -140,7 +140,7 @@ void reverse(int[] arr) {
思路是类似的,只要通过另一条对角线镜像对称矩阵,然后再反转每一行,就得到了逆时针旋转矩阵的结果:
-
+
翻译成代码如下:
@@ -174,7 +174,7 @@ void reverse(int[] arr) { /* 见上文 */}
但接下来我们讲一下力扣第 54 题「螺旋矩阵」,看一看二维矩阵可以如何花式遍历:
-
+
函数签名如下:
@@ -184,11 +184,11 @@ List spiralOrder(int[][] matrix)
**解题的核心思路是按照右、下、左、上的顺序遍历数组,并使用四个变量圈定未遍历元素的边界**:
-
+
随着螺旋遍历,相应的边界会收缩,直到螺旋遍历完整个数组:
-
+
只要有了这个思路,翻译出代码就很容易了:
@@ -242,7 +242,7 @@ List spiralOrder(int[][] matrix) {
力扣第 59 题「螺旋矩阵 II」也是类似的题目,只不过是反过来,让你按照螺旋的顺序生成矩阵:
-
+
函数签名如下:
@@ -330,4 +330,4 @@ int[][] generateMatrix(int n) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/351円233円206円345円220円210円345円210円222円345円210円206円.md" "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/351円233円206円345円220円210円345円210円222円345円210円206円.md"
index a7f29ef3b2..da52cc6e74 100644
--- "a/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/351円233円206円345円220円210円345円210円222円345円210円206円.md"
+++ "b/347円256円227円346円263円225円346円200円235円347円273円264円347円263円273円345円210円227円/351円233円206円345円220円210円345円210円222円345円210円206円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -55,13 +55,13 @@ boolean canPartitionKSubsets(int[] nums, int k);
3、排列、组合总数的计算公式:
-
+
好,现在我问一个问题,这个排列公式 `P(n, k)` 是如何推导出来的?为了搞清楚这个问题,我需要讲一点组合数学的知识。
排列组合问题的各种变体都可以抽象成「球盒模型」,`P(n, k)` 就可以抽象成下面这个场景:
-
+
即,将 `n` 个标记了不同序号的球(标号为了体现顺序的差异),放入 `k` 个标记了不同序号的盒子中(其中 `n>= k`,每个盒子最终都装有恰好一个球),共有 `P(n, k)` 种不同的方法。
@@ -71,7 +71,7 @@ boolean canPartitionKSubsets(int[] nums, int k);
这样,第一个盒子可以选择 `n` 个球中的任意一个,然后你需要让剩下 `k - 1` 个盒子在 `n - 1` 个球中选择:
-
+
**另外,你也可以站在球的视角**,因为并不是每个球都会被装进盒子,所以球的视角分两种情况:
@@ -81,11 +81,11 @@ boolean canPartitionKSubsets(int[] nums, int k);
结合上述两种情况,可以得到:
-
+
你看,两种视角得到两个不同的递归式,但这两个递归式解开的结果都是我们熟知的阶乘形式:
-
+
至于如何解递归式,涉及数学的内容比较多,这里就不做深入探讨了,有兴趣的读者可以自行学习组合数学相关知识。
@@ -101,11 +101,11 @@ boolean canPartitionKSubsets(int[] nums, int k);
**视角一,如果我们切换到这 `n` 个数字的视角,每个数字都要选择进入到 `k` 个桶中的某一个**。
-
+
**视角二,如果我们切换到这 `k` 个桶的视角,对于每个桶,都要遍历 `nums` 中的 `n` 个数字,然后选择是否将当前遍历到的数字装进自己这个桶里**。
-
+
你可能问,这两种视角有什么不同?
@@ -389,11 +389,11 @@ boolean backtrack(int k, int bucket,
那么,比如下面这种情况,`target = 5`,算法会在第一个桶里面装 `1, 4`:
-
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `2, 3`:
-
+
然后以此类推,对后面的元素进行穷举,凑出若干个和为 5 的桶(子集)。
@@ -401,11 +401,11 @@ boolean backtrack(int k, int bucket,
回溯算法会回溯到第一个桶,重新开始穷举,现在它知道第一个桶里装 `1, 4` 是不可行的,它会尝试把 `2, 3` 装到第一个桶里:
-
+
现在第一个桶装满了,就开始装第二个桶,算法会装入 `1, 4`:
-
+
好,到这里你应该看出来问题了,这种情况其实和之前的那种情况是一样的。也就是说,到这里你其实已经知道不需要再穷举了,必然凑不出来和为 `target` 的 `k` 个子集。
@@ -570,4 +570,4 @@ boolean backtrack(int k, int bucket,
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/LRU347円256円227円346円263円225円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/LRU347円256円227円346円263円225円.md"
index 70f4b4233a..e7529426a8 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/LRU347円256円227円346円263円225円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/LRU347円256円227円346円263円225円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -30,17 +30,17 @@ LRU 缓存淘汰算法就是一种常用策略。LRU 的全称是 Least Recently
举个简单的例子,安卓手机都可以把软件放到后台运行,比如我先后打开了「设置」「手机管家」「日历」,那么现在他们在后台排列的顺序是这样的:
-
+
但是这时候如果我访问了一下「设置」界面,那么「设置」就会被提前到第一个,变成这样:
-
+
假设我的手机只允许我同时开 3 个应用程序,现在已经满了。那么如果我新开了一个应用「时钟」,就必须关闭一个应用为「时钟」腾出一个位置,关那个呢?
按照 LRU 的策略,就关最底下的「手机管家」,因为那是最久未使用的,然后把新开的应用放到最上面:
-
+
现在你应该理解 LRU(Least Recently Used)策略了。当然还有其他缓存淘汰策略,比如不要按访问的时序来淘汰,而是按访问频率(LFU 策略)来淘汰等等,各有应用场景。本文讲解 LRU 算法策略。
@@ -101,7 +101,7 @@ cache.put(1, 4);
LRU 缓存算法的核心数据结构就是哈希链表,双向链表和哈希表的结合体。这个数据结构长这样:
-
+
借助这个结构,我们来逐一分析上面的 3 个条件:
@@ -267,7 +267,7 @@ public int get(int key) {
`put` 方法稍微复杂一些,我们先来画个图搞清楚它的逻辑:
-
+
这样我们可以轻松写出 `put` 方法的代码:
@@ -377,7 +377,7 @@ class LRUCache {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/k344円270円252円344円270円200円347円273円204円345円217円215円350円275円254円351円223円276円350円241円250円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/k344円270円252円344円270円200円347円273円204円345円217円215円350円275円254円351円223円276円350円241円250円.md"
index 8e8c9deae3..2a7be82337 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/k344円270円252円344円270円200円347円273円204円345円217円215円350円275円254円351円223円276円350円241円250円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/k344円270円252円344円270円200円347円273円204円345円217円215円350円275円254円351円223円276円350円241円250円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -25,7 +25,7 @@
本文要解决力扣第 25 题「K 个一组翻转链表」,题目不难理解:
-
+
这个问题经常在面经中看到,而且力扣上难度是 Hard,它真的有那么难吗?
@@ -37,11 +37,11 @@
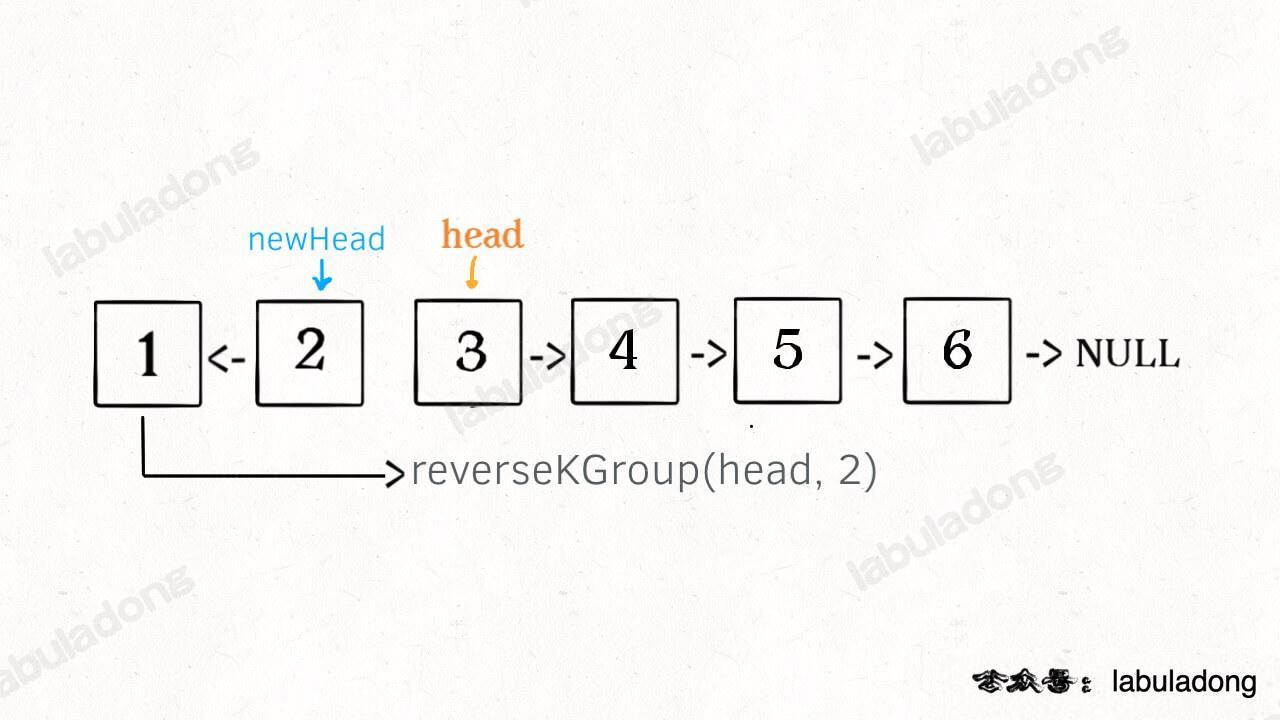
什么叫递归性质?直接上图理解,比如说我们对这个链表调用 `reverseKGroup(head, 2)`,即以 2 个节点为一组反转链表:
-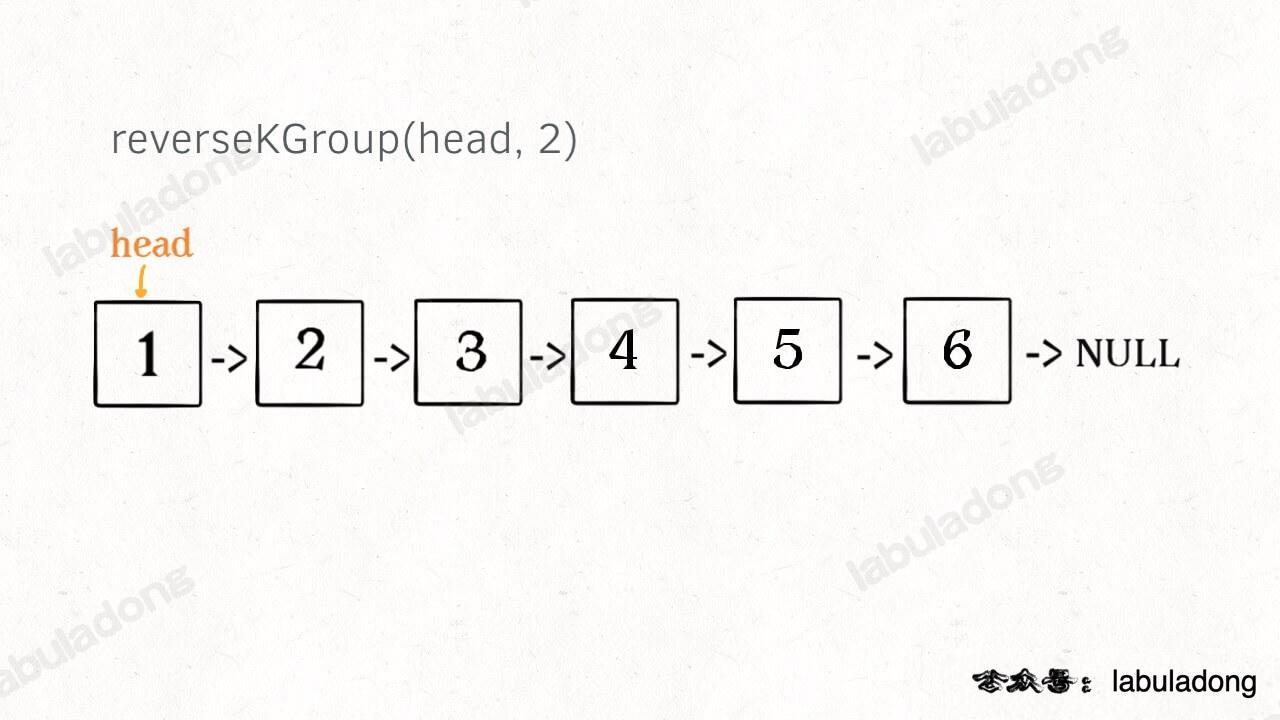
+
如果我设法把前 2 个节点反转,那么后面的那些节点怎么处理?后面的这些节点也是一条链表,而且规模(长度)比原来这条链表小,这就叫**子问题**。
-
+
我们可以把原先的 `head` 指针移动到后面这一段链表的开头,然后继续递归调用 `reverseKGroup(head, 2)`,因为子问题(后面这部分链表)和原问题(整条链表)的结构完全相同,这就是所谓的递归性质。
@@ -49,15 +49,15 @@
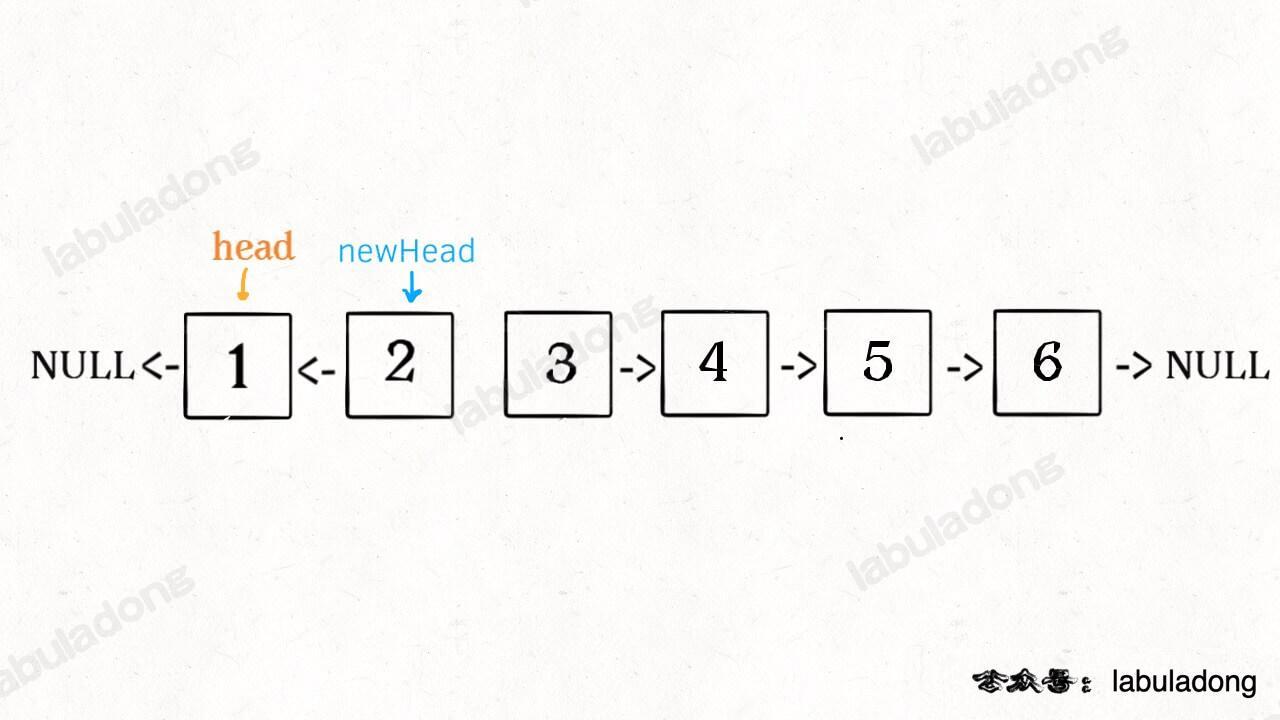
**1、先反转以 `head` 开头的 `k` 个元素**。
-
+
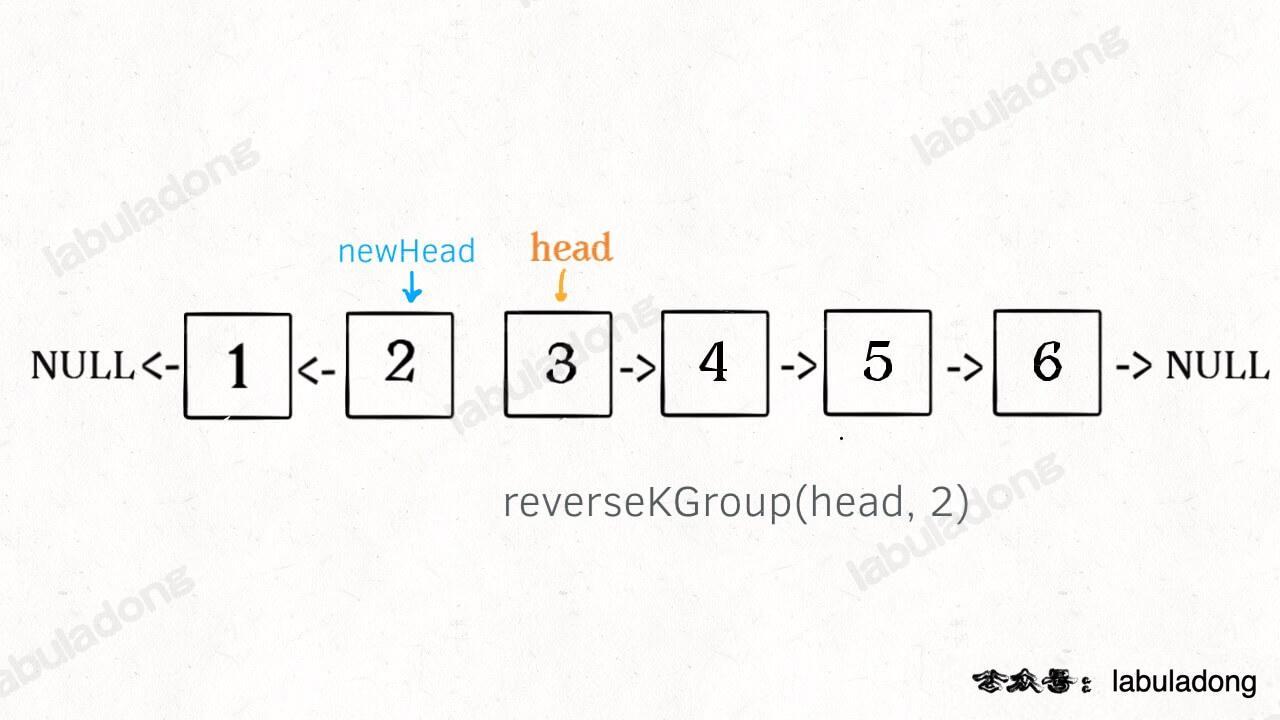
**2、将第 `k + 1` 个元素作为 `head` 递归调用 `reverseKGroup` 函数**。
-
+
**3、将上述两个过程的结果连接起来**。
-
+
整体思路就是这样了,最后一点值得注意的是,递归函数都有个 base case,对于这个问题是什么呢?
@@ -87,7 +87,7 @@ ListNode reverse(ListNode a) {
算法执行的过程如下 GIF 所示::
-
+
这次使用迭代思路来实现的,借助动画理解应该很容易。
@@ -135,11 +135,11 @@ ListNode reverseKGroup(ListNode head, int k) {
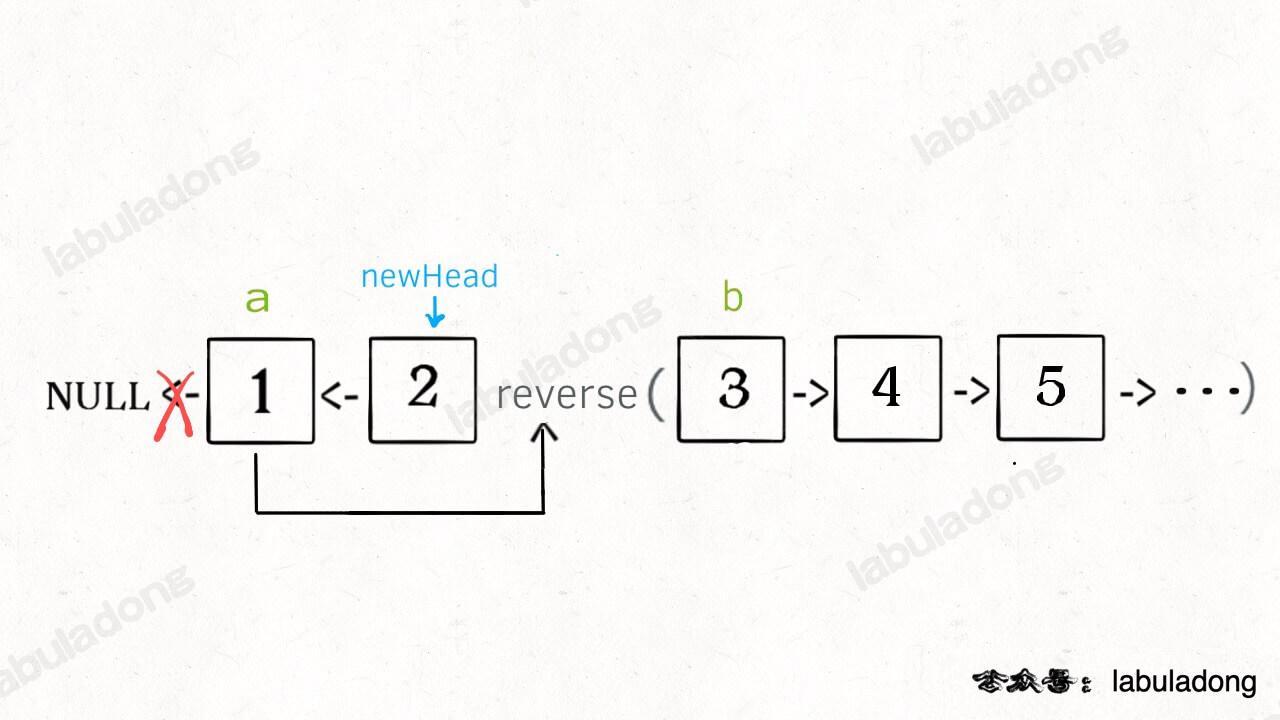
解释一下 `for` 循环之后的几句代码,注意 `reverse` 函数是反转区间 `[a, b)`,所以情形是这样的:
-
+
递归部分就不展开了,整个函数递归完成之后就是这个结果,完全符合题意:
-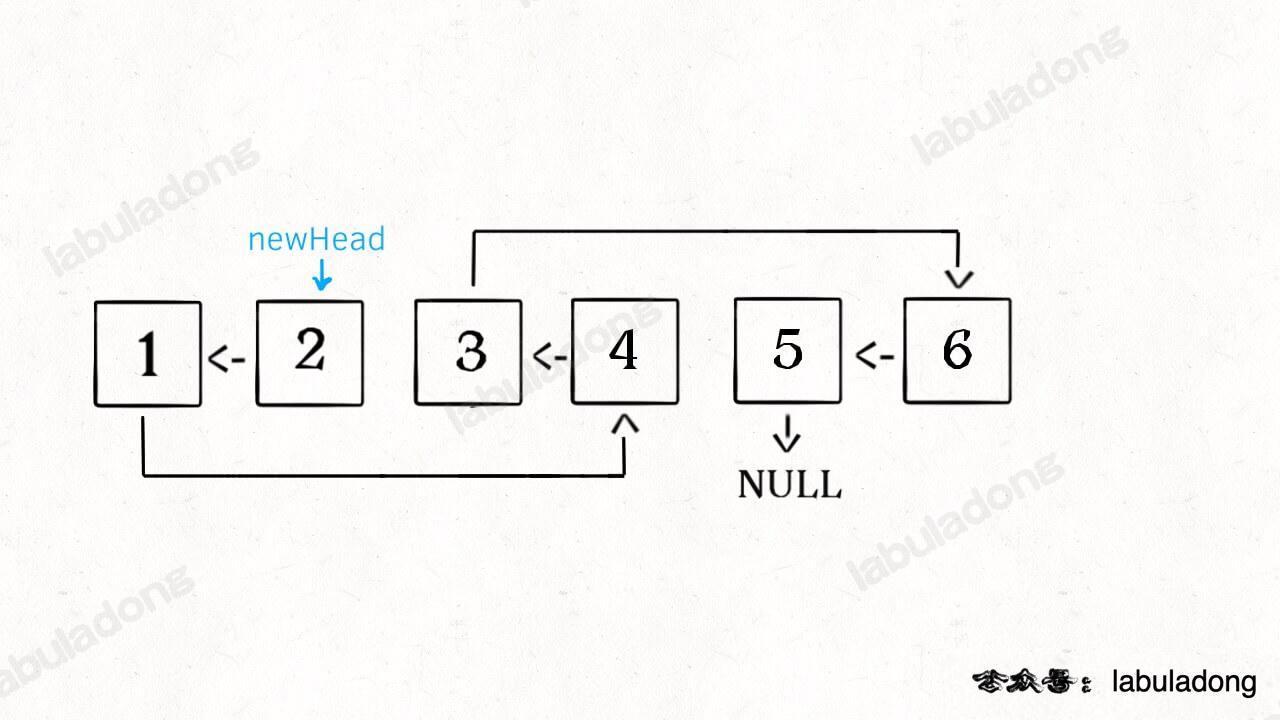
+
### 三、最后说两句
@@ -181,7 +181,7 @@ ListNode reverseKGroup(ListNode head, int k) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円270円200円350円241円214円344円273円243円347円240円201円350円247円243円345円206円263円347円232円204円346円231円272円345円212円233円351円242円230円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円270円200円350円241円214円344円273円243円347円240円201円350円247円243円345円206円263円347円232円204円346円231円272円345円212円233円351円242円230円.md"
index 21e796f0df..e0f39f96fd 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円270円200円350円241円214円344円273円243円347円240円201円350円247円243円345円206円263円347円232円204円346円231円272円345円212円233円351円242円230円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円270円200円350円241円214円344円273円243円347円240円201円350円247円243円345円206円263円347円232円204円346円231円272円345円212円233円351円242円230円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -161,7 +161,7 @@ int bulbSwitch(int n) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円345円210円244円345円256円232円345円255円220円345円272円217円345円210円227円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円345円210円244円345円256円232円345円255円220円345円272円217円345円210円227円.md"
index 9feade99ed..9b550ae9ce 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円345円210円244円345円256円232円345円255円220円345円272円217円345円210円227円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円346円237円245円346円211円276円345円210円244円345円256円232円345円255円220円345円272円217円345円210円227円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -57,7 +57,7 @@ boolean isSubsequence(String s, String t) {
其思路也非常简单,利用双指针 `i, j` 分别指向 `s, t`,一边前进一边匹配子序列:
-
+
读者也许会问,这不就是最优解法了吗,时间复杂度只需 O(N),N 为 `t` 的长度。
@@ -89,15 +89,15 @@ for (int i = 0; i < n; i++) { } ``` - + 比如对于这个情况,匹配了 "ab",应该匹配 "c" 了: - + 按照之前的解法,我们需要 `j` 线性前进扫描字符 "c",但借助 `index` 中记录的信息,**可以二分搜索 `index[c]` 中比 j 大的那个索引**,在上图的例子中,就是在 `[0,2,6]` 中搜索比 4 大的那个索引: - + 这样就可以直接得到下一个 "c" 的索引。现在的问题就是,如何用二分查找计算那个恰好比 4 大的索引呢?答案是,寻找左侧边界的二分搜索就可以做到。 @@ -163,7 +163,7 @@ boolean isSubsequence(String s, String t) { 算法执行的过程是这样的: - + 可见借助二分查找,算法的效率是可以大幅提升的。 @@ -234,7 +234,7 @@ int left_bound(ArrayList arr, int target) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円350円277円220円347円224円250円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円350円277円220円347円224円250円.md"
index 6844e236ea..8aa5e464a9 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円350円277円220円347円224円250円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/344円272円214円345円210円206円350円277円220円347円224円250円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -71,7 +71,7 @@ int left_bound(int[] nums, int target) {
如果画一个图,就是这样:
-
+
「搜索右侧边界」的二分搜索算法的具体代码实现如下:
@@ -98,7 +98,7 @@ int right_bound(int[] nums, int target) {
输入同上,那么算法就会返回索引 4,如果画一个图,就是这样:
-
+
好,上述内容都属于复习,我想读到这里的读者应该都能理解。记住上述的图像,所有能够抽象出上述图像的问题,都可以使用二分搜索解决。
@@ -112,7 +112,7 @@ int right_bound(int[] nums, int target) {
- [二分搜索怎么用?我和快手面试官进行了深度探讨](https://labuladong.github.io/article/fname.html?fname=二分分割子数组)
- [我写了首诗,把二分搜索算法变成了默写题](https://labuladong.github.io/article/fname.html?fname=二分查找详解)
- [我的刷题心得](https://labuladong.github.io/article/fname.html?fname=算法心得)
- - [用算法打败算法 ](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
+ - [用算法打败算法](https://labuladong.github.io/article/fname.html?fname=PDF中的算法)
- [经典动态规划:高楼扔鸡蛋](https://labuladong.github.io/article/fname.html?fname=高楼扔鸡蛋问题)
- [讲两道常考的阶乘算法题](https://labuladong.github.io/article/fname.html?fname=阶乘题目)
@@ -140,4 +140,4 @@ int right_bound(int[] nums, int target) {
应合作方要求,本文不便在此发布,请扫码关注回复关键词「二分」或 [点这里](https://appktavsiei5995.pc.xiaoe-tech.com/detail/i_627cce2de4b01a4851fe0ed1/1) 查看:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円210円244円346円226円255円345円233円236円346円226円207円351円223円276円350円241円250円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円210円244円346円226円255円345円233円236円346円226円207円351円223円276円350円241円250円.md"
index 1fd95f20d8..374d362453 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円210円244円346円226円255円345円233円236円346円226円207円351円223円276円350円241円250円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円210円244円346円226円255円345円233円236円346円226円207円351円223円276円350円241円250円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -147,7 +147,7 @@ boolean traverse(ListNode right) {
这么做的核心逻辑是什么呢?**实际上就是把链表节点放入一个栈,然后再拿出来,这时候元素顺序就是反的**,只不过我们利用的是递归函数的堆栈而已,如下 GIF 所示:
-
+
当然,无论造一条反转链表还是利用后序遍历,算法的时间和空间复杂度都是 O(N)。下面我们想想,能不能不用额外的空间,解决这个问题呢?
@@ -167,7 +167,7 @@ while (fast != null && fast.next != null) {
// slow 指针现在指向链表中点
```
-
+
**2、如果`fast`指针没有指向`null`,说明链表长度为奇数,`slow`还要再前进一步**:
@@ -176,7 +176,7 @@ if (fast != null)
slow = slow.next;
```
-
+
**3、从`slow`开始反转后面的链表,现在就可以开始比较回文串了**:
@@ -193,7 +193,7 @@ while (right != null) {
return true;
```
-
+
至此,把上面 3 段代码合在一起就高效地解决这个问题了,其中 `reverse` 函数很容易实现:
@@ -235,7 +235,7 @@ ListNode reverse(ListNode head) {
算法过程如下 GIF 所示:
-
+
算法总体的时间复杂度 O(N),空间复杂度 O(1),已经是最优的了。
@@ -243,7 +243,7 @@ ListNode reverse(ListNode head) {
其实这个问题很好解决,关键在于得到`p, q`这两个指针位置:
-
+
这样,只要在函数 return 之前加一段代码即可恢复原先链表顺序:
@@ -282,7 +282,7 @@ p.next = reverse(q);
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円220円215円344円272円272円351円227円256円351円242円230円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円220円215円344円272円272円351円227円256円351円242円230円.md"
index 6c6e6e7a82..ad6653b80e 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円220円215円344円272円272円351円227円256円351円242円230円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円220円215円344円272円272円351円227円256円351円242円230円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -35,7 +35,7 @@
如果把每个人看做图中的节点,「认识」这种关系看做是节点之间的有向边,那么名人就是这幅图中一个特殊的节点:
-
+
**这个节点没有一条指向其他节点的有向边;且其他所有节点都有一条指向这个节点的有向边**。
@@ -65,7 +65,7 @@ int findCelebrity(int[][] graph);
比如输入的邻接矩阵长这样:
-
+
那么算法应该返回 2。
@@ -145,7 +145,7 @@ int findCelebrity(int n) {
如果把人比作节点,红色的有向边表示不认识,绿色的有向边表示认识,那么两个人的关系无非是如下四种情况:
-
+
不妨认为这两个人的编号分别是 `cand` 和 `other`,然后我们逐一分析每种情况,看看怎么排除掉一个人。
@@ -271,4 +271,4 @@ int findCelebrity(int n) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円255円220円351円233円206円346円216円222円345円210円227円347円273円204円345円220円210円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円255円220円351円233円206円346円216円222円345円210円227円347円273円204円345円220円210円.md"
index 6ad028e2e6..34d72092fa 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円255円220円351円233円206円346円216円222円345円210円227円347円273円204円345円220円210円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円255円220円351円233円206円346円216円222円345円210円227円347円273円204円345円220円210円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -62,9 +62,9 @@
具体来说,你需要先阅读并理解前文 [回溯算法核心套路](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版),然后记住如下子集问题和排列问题的回溯树,就可以解决所有排列组合子集相关的问题:
-
+
-
+
为什么只要记住这两种树形结构就能解决所有相关问题呢?
@@ -96,11 +96,11 @@ List> subsets(int[] nums)
然后,在 `S_0` 的基础上生成元素个数为 1 的所有子集,我称为 `S_1`:
-
+
接下来,我们可以在 `S_1` 的基础上推导出 `S_2`,即元素个数为 2 的所有子集:
-
+
为什么集合 `[2]` 只需要添加 `3`,而不添加前面的 `1` 呢?
@@ -112,7 +112,7 @@ List> subsets(int[] nums)
整个推导过程就是这样一棵树:
-
+
注意这棵树的特性:
@@ -120,7 +120,7 @@ List> subsets(int[] nums)
你比如大小为 2 的子集就是这一层节点的值:
-
+
> **PS:注意,本文之后所说「节点的值」都是指节点和根节点之间树枝上的元素,且将根节点认为是第 0 层**。
@@ -159,7 +159,7 @@ void backtrack(int[] nums, int start) {
看过前文 [回溯算法核心框架](https://labuladong.github.io/article/fname.html?fname=回溯算法详解修订版) 的读者应该很容易理解这段代码吧,我们使用 `start` 参数控制树枝的生长避免产生重复的子集,用 `track` 记录根节点到每个节点的路径的值,同时在前序位置把每个节点的路径值收集起来,完成回溯树的遍历就收集了所有子集:
-
+
最后,`backtrack` 函数开头看似没有 base case,会不会进入无限递归?
@@ -197,7 +197,7 @@ List> combine(int n, int k)
还是以 `nums = [1,2,3]` 为例,刚才让你求所有子集,就是把所有节点的值都收集起来;**现在你只需要把第 2 层(根节点视为第 0 层)的节点收集起来,就是大小为 2 的所有组合**:
-
+
反映到代码上,只需要稍改 base case,控制算法仅仅收集第 `k` 层节点的值即可:
@@ -264,7 +264,7 @@ List> permute(int[] nums)
标准全排列可以抽象成如下这棵多叉树:
-
+
我们用 `used` 数组标记已经在路径上的元素避免重复选择,然后收集所有叶子节点上的值,就是所有全排列的结果:
@@ -360,7 +360,7 @@ List> subsetsWithDup(int[] nums)
按照之前的思路画出子集的树形结构,显然,两条值相同的相邻树枝会产生重复:
-
+
```
[
@@ -373,7 +373,7 @@ List> subsetsWithDup(int[] nums)
所以我们需要进行剪枝,如果一个节点有多条值相同的树枝相邻,则只遍历第一条,剩下的都剪掉,不要去遍历:
-
+
**体现在代码上,需要先进行排序,让相同的元素靠在一起,如果发现 `nums[i] == nums[i-1]`,则跳过**:
@@ -586,15 +586,15 @@ if (i> 0 && nums[i] == nums[i - 1] && !used[i - 1]) {
比如输入 `nums = [2,2',2'']`,产生的回溯树如下:
-
+
如果用绿色树枝代表 `backtrack` 函数遍历过的路径,红色树枝代表剪枝逻辑的触发,那么 `!used[i - 1]` 这种剪枝逻辑得到的回溯树长这样:
-
+
而 `used[i - 1]` 这种剪枝逻辑得到的回溯树如下:
-
+
可以看到,`!used[i - 1]` 这种剪枝逻辑剪得干净利落,而 `used[i - 1]` 这种剪枝逻辑虽然也能得到无重结果,但它剪掉的树枝较少,存在的无效计算较多,所以效率会差一些。
@@ -634,7 +634,7 @@ void backtrack(int[] nums, LinkedList track) {
这个思路也是对的,设想一个节点出现了相同的树枝:
-
+
如果不作处理,这些相同树枝下面的子树也会长得一模一样,所以会出现重复的排列。
@@ -682,7 +682,7 @@ void backtrack(int[] nums, int start) {
这个 `i` 从 `start` 开始,那么下一层回溯树就是从 `start + 1` 开始,从而保证 `nums[start]` 这个元素不会被重复使用:
-
+
那么反过来,如果我想让每个元素被重复使用,我只要把 `i + 1` 改成 `i` 即可:
@@ -700,7 +700,7 @@ void backtrack(int[] nums, int start) {
这相当于给之前的回溯树添加了一条树枝,在遍历这棵树的过程中,一个元素可以被无限次使用:
-
+
当然,这样这棵回溯树会永远生长下去,所以我们的递归函数需要设置合适的 base case 以结束算法,即路径和大于 `target` 时就没必要再遍历下去了。
@@ -960,7 +960,7 @@ void backtrack(int[] nums) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円256円211円346円216円222円344円274円232円350円256円256円345円256円244円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円256円211円346円216円222円344円274円232円350円256円256円345円256円244円.md"
index 49d33c6111..23c8028ab2 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円256円211円346円216円222円344円274円232円350円256円256円345円256円244円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円256円211円346円216円222円344円274円232円350円256円256円345円256円244円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -108,13 +108,13 @@ int minMeetingRooms(int[][] meetings);
我们首先把这些会议的时间区间进行投影:
-
+
红色的点代表每个会议的开始时间点,绿色的点代表每个会议的结束时间点。
现在假想有一条带着计数器的线,在时间线上从左至右进行扫描,每遇到红色的点,计数器 `count` 加一,每遇到绿色的点,计数器 `count` 减一:
-
+
**这样一来,每个时刻有多少个会议在同时进行,就是计数器 `count` 的值,`count` 的最大值,就是需要申请的会议室数量**。
@@ -126,7 +126,7 @@ int minMeetingRooms(int[][] meetings);
首先,对区间进行投影,就相当于对每个区间的起点和终点分别进行排序:
-
+
```java
int minMeetingRooms(int[][] meetings) {
@@ -199,4 +199,4 @@ int minMeetingRooms(int[][] meetings) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円262円233円345円261円277円351円242円230円347円233円256円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円262円233円345円261円277円351円242円230円347円233円256円.md"
index 083421a374..ac5750c79b 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円262円233円345円261円277円351円242円230円347円233円256円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円262円233円345円261円277円351円242円230円347円233円256円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -109,7 +109,7 @@ int numIslands(char[][] grid);
比如说题目给你输入下面这个 `grid` 有四片岛屿,算法应该返回 4:
-
+
思路很简单,关键在于如何寻找并标记「岛屿」,这就要 DFS 算法发挥作用了,我们直接看解法代码:
@@ -179,7 +179,7 @@ int closedIsland(int[][] grid)
比如题目给你输入如下这个二维矩阵:
-
+
算法返回 2,只有图中灰色部分的 `0` 是四周全都被海水包围着的「封闭岛屿」。
@@ -288,7 +288,7 @@ int maxAreaOfIsland(int[][] grid)
比如题目给你输入如下一个二维矩阵:
-
+
其中面积最大的是橘红色的岛屿,算法返回它的面积 6。
@@ -339,7 +339,7 @@ int dfs(int[][] grid, int i, int j) {
如果说前面的题目都是模板题,那么力扣第 1905 题「统计子岛屿」可能得动动脑子了:
-
+
**这道题的关键在于,如何快速判断子岛屿**?肯定可以借助 [Union Find 并查集算法](https://labuladong.github.io/article/fname.html?fname=UnionFind算法详解) 来判断,不过本文重点在 DFS 算法,就不展开并查集算法了。
@@ -409,7 +409,7 @@ int numDistinctIslands(int[][] grid)
比如题目输入下面这个二维矩阵:
-
+
其中有四个岛屿,但是左下角和右上角的岛屿形状相同,所以不同的岛屿共有三个,算法返回 3。
@@ -433,7 +433,7 @@ void dfs(int[][] grid, int i, int j) {
所以,遍历顺序从某种意义上说就可以用来描述岛屿的形状,比如下图这两个岛屿:
-
+
假设它们的遍历顺序是:
@@ -531,4 +531,4 @@ int numDistinctIslands(int[][] grid) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
\ No newline at end of file
+
\ No newline at end of file
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円272円247円344円275円215円350円260円203円345円272円246円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円272円247円344円275円215円350円260円203円345円272円246円.md"
index 404ea6658e..44f2811c3c 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円272円247円344円275円215円350円260円203円345円272円246円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/345円272円247円344円275円215円350円260円203円345円272円246円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -131,7 +131,7 @@ private int distance(int[] intv) {
「虚拟线段」其实就是为了将所有座位表示为一个线段:
-
+
有了上述铺垫,主要 API `seat` 和 `leave` 就可以写了:
@@ -170,7 +170,7 @@ public void leave(int p) {
}
```
-
+
至此,算法就基本实现了,代码虽多,但思路很简单:找最长的线段,从中间分隔成两段,中点就是 `seat()` 的返回值;找 `p` 的左右线段,合并成一个线段,这就是 `leave(p)` 的逻辑。
@@ -178,11 +178,11 @@ public void leave(int p) {
但是,题目要求多个选择时选择索引最小的那个座位,我们刚才忽略了这个问题。比如下面这种情况会出错:
-
+
现在有序集合里有线段 `[0,4]` 和 `[4,9]`,那么最长线段 `longest` 就是后者,按照 `seat` 的逻辑,就会分割 `[4,9]`,也就是返回座位 6。但正确答案应该是座位 2,因为 2 和 6 都满足最大化相邻考生距离的条件,二者应该取较小的。
-
+
**遇到题目的这种要求,解决方式就是修改有序数据结构的排序方式**。具体到这个问题,就是修改 `TreeMap` 的比较函数逻辑:
@@ -210,7 +210,7 @@ private int distance(int[] intv) {
}
```
-
+
这样,`[0,4]` 和 `[4,9]` 的 `distance` 值就相等了,算法会比较二者的索引,取较小的线段进行分割。到这里,这道算法题目算是完全解决了。
@@ -232,7 +232,7 @@ private int distance(int[] intv) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円211円223円345円215円260円347円264円240円346円225円260円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円211円223円345円215円260円347円264円240円346円225円260円.md"
index 19cb54bf3f..59a99ffe48 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円211円223円345円215円260円347円264円240円346円225円260円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円211円223円345円215円260円347円264円240円346円225円260円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -94,7 +94,7 @@ boolean isPrime(int n) {
Wikipedia 的这个 GIF 很形象:
-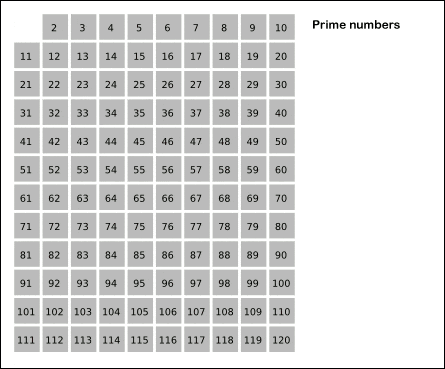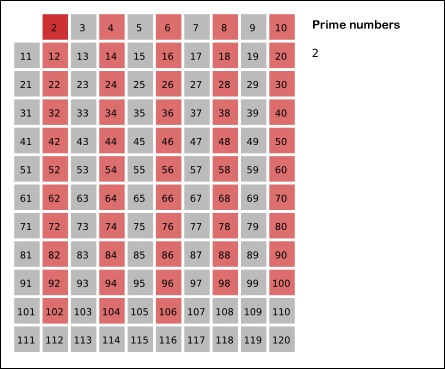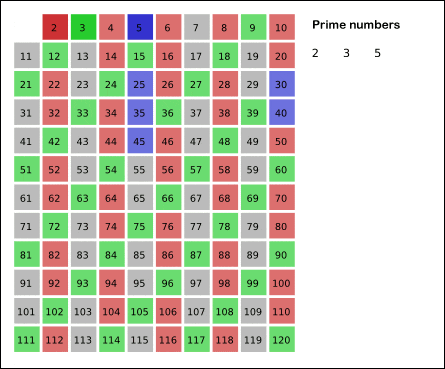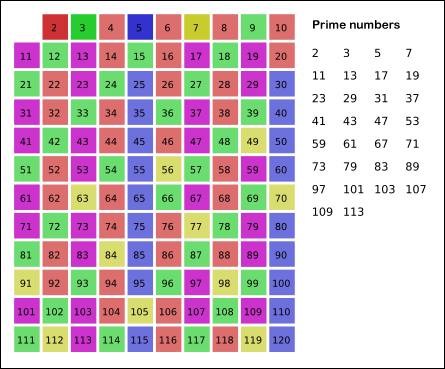
+
看到这里,你是否有点明白这个排除法的逻辑了呢?先看我们的第一版代码:
@@ -205,7 +205,7 @@ int countPrimes(int n) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円216円245円351円233円250円346円260円264円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円216円245円351円233円250円346円260円264円.md"
index f8c36f201a..1eb01f02d6 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円216円245円351円233円250円346円260円264円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円216円245円351円233円250円346円260円264円.md"
@@ -9,9 +9,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -28,7 +28,7 @@
先看一下题目:
-
+
就是用一个数组表示一个条形图,问你这个条形图最多能接多少水。
@@ -44,7 +44,7 @@ int trap(int[] height);
这么一想,可以发现这道题的思路其实很简单。具体来说,仅仅对于位置 `i`,能装下多少水呢?
-
+
能装 2 格水,因为 `height[i]` 的高度为 0,而这里最多能盛 2 格水,2-0=2。
@@ -62,9 +62,9 @@ water[i] = min(
```
-
+
-
+
这就是本问题的核心思路,我们可以简单写一个暴力算法:
@@ -181,7 +181,7 @@ int trap(int[] height) {
res += Math.min(l_max[i], r_max[i]) - height[i];
```
-
+
但是双指针解法中,`l_max` 和 `r_max` 代表的是 `height[0..left]` 和 `height[right..end]` 的最高柱子高度。比如这段代码:
@@ -192,13 +192,13 @@ if (l_max < r_max) { } ``` - + 此时的 `l_max` 是 `left` 指针左边的最高柱子,但是 `r_max` 并不一定是 `left` 指针右边最高的柱子,这真的可以得到正确答案吗? 其实这个问题要这么思考,我们只在乎 `min(l_max, r_max)`。**对于上图的情况,我们已经知道 `l_max < r_max` 了,至于这个 `r_max` 是不是右边最大的,不重要。重要的是 `height[i]` 能够装的水只和较低的 `l_max` 之差有关**: - + 这样,接雨水问题就解决了。 @@ -206,7 +206,7 @@ if (l_max < r_max) { 下面我们看一道和接雨水问题非常类似的题目,力扣第 11 题「盛最多水的容器」: - + 函数签名如下: @@ -284,7 +284,7 @@ if (height[left] < height[right]) { **《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**: - + ======其他语言代码====== diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円260円264円345円241円230円346円212円275円346円240円267円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円260円264円345円241円230円346円212円275円346円240円267円.md" index 756961d448..297b674620 100644 --- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円260円264円345円241円230円346円212円275円346円240円267円.md" +++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/346円260円264円345円241円230円346円212円275円346円240円267円.md" @@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -62,7 +62,7 @@ int getRandom(ListNode head) {
**证明**:假设总共有 `n` 个元素,我们要的随机性无非就是每个元素被选择的概率都是 `1/n` 对吧,那么对于第 `i` 个元素,它被选择的概率就是:
-
+
第 `i` 个元素被选择的概率是 `1/i`,第 `i+1` 次不被替换的概率是 `1 - 1/(i+1)`,以此类推,相乘就是第 `i` 个元素最终被选中的概率,就是 `1/n`。
@@ -100,7 +100,7 @@ int[] getRandom(ListNode head, int k) {
对于数学证明,和上面区别不大:
-
+
因为虽然每次更新选择的概率增大了 `k` 倍,但是选到具体第 `i` 个元素的概率还是要乘 `1/k`,也就回到了上一个推导。
@@ -132,7 +132,7 @@ int[] getRandom(ListNode head, int k) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/347円274円272円345円244円261円345円222円214円351円207円215円345円244円215円347円232円204円345円205円203円347円264円240円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/347円274円272円345円244円261円345円222円214円351円207円215円345円244円215円347円232円204円345円205円203円347円264円240円.md"
index 72ecd34d98..b9828e2e2b 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/347円274円272円345円244円261円345円222円214円351円207円215円345円244円215円347円232円204円345円205円203円347円264円240円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/347円274円272円345円244円261円345円222円214円351円207円215円345円244円215円347円232円204円345円205円203円347円264円240円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -56,15 +56,15 @@ O(N) 的时间复杂度遍历数组是无法避免的,所以我们可以想想
**通过将每个索引对应的元素变成负数,以表示这个索引被对应过一次了**,算法过程如下 GIF 所示:
-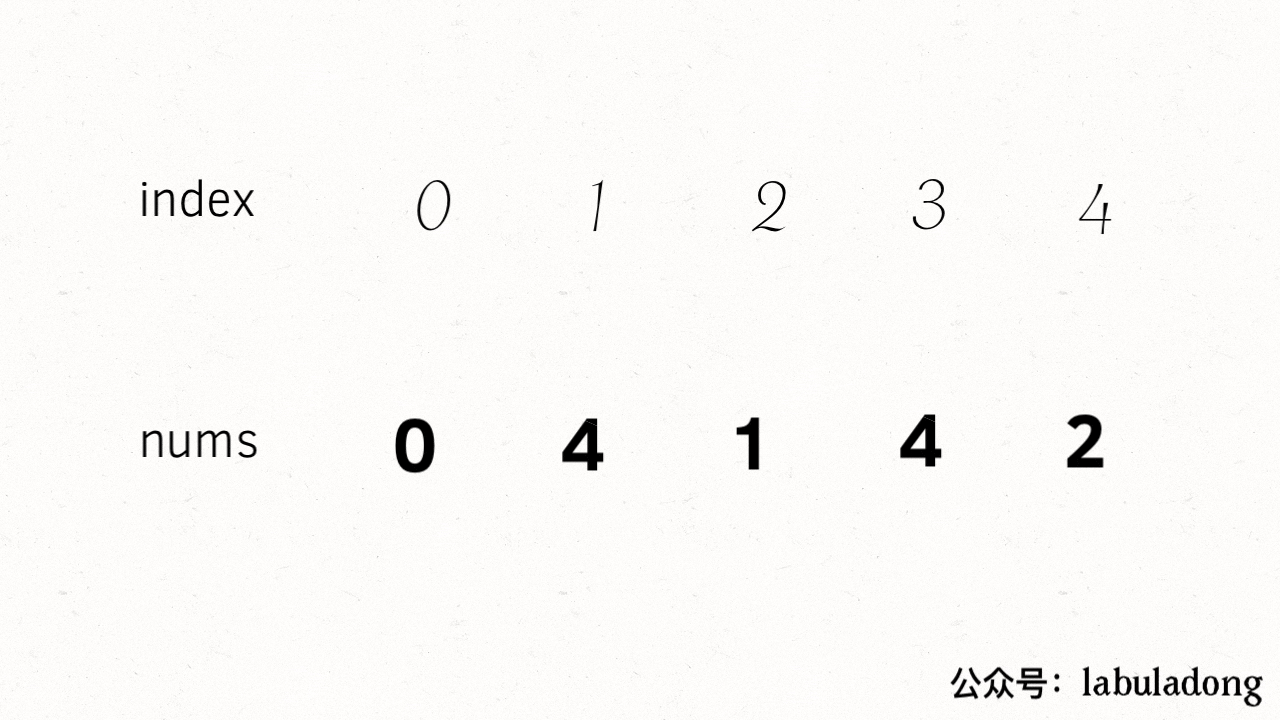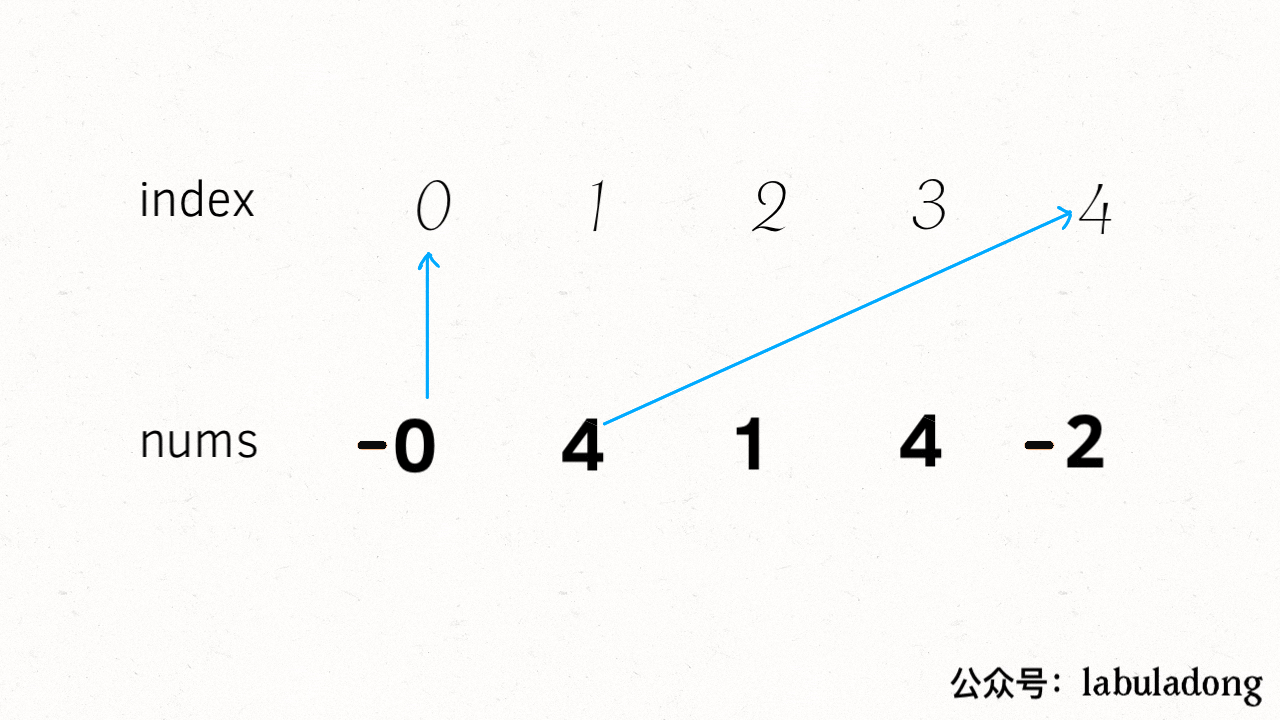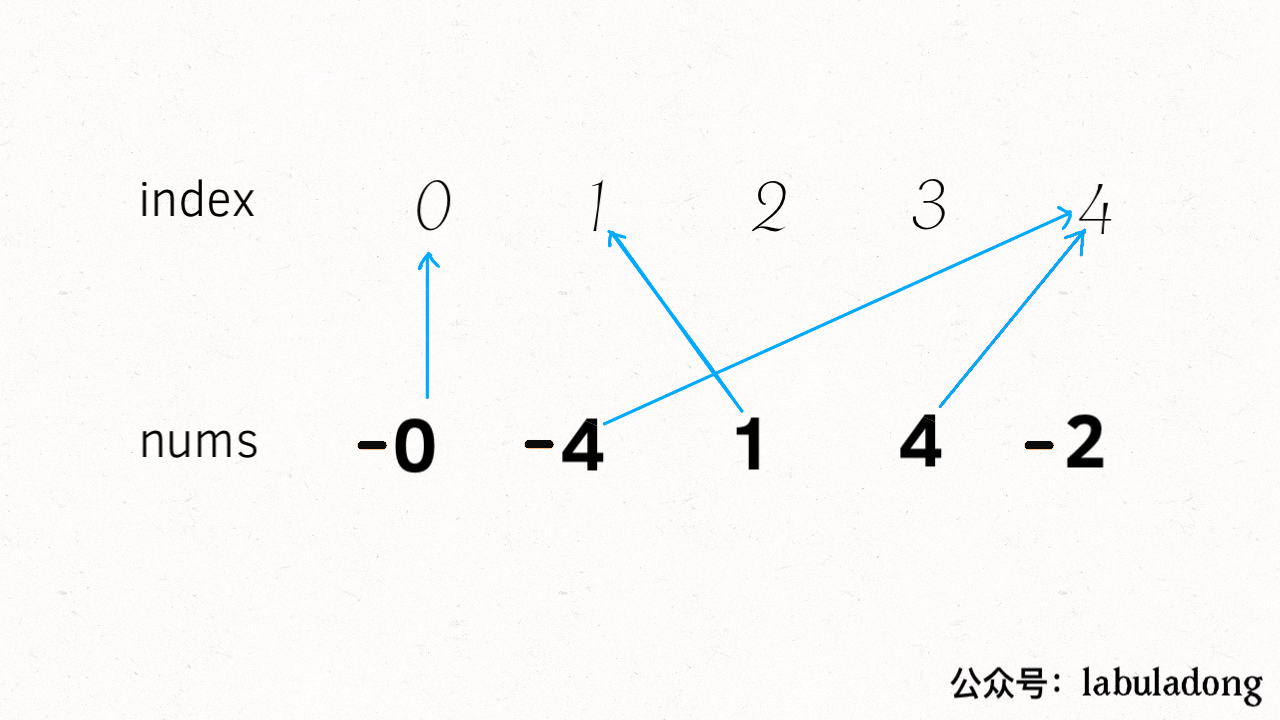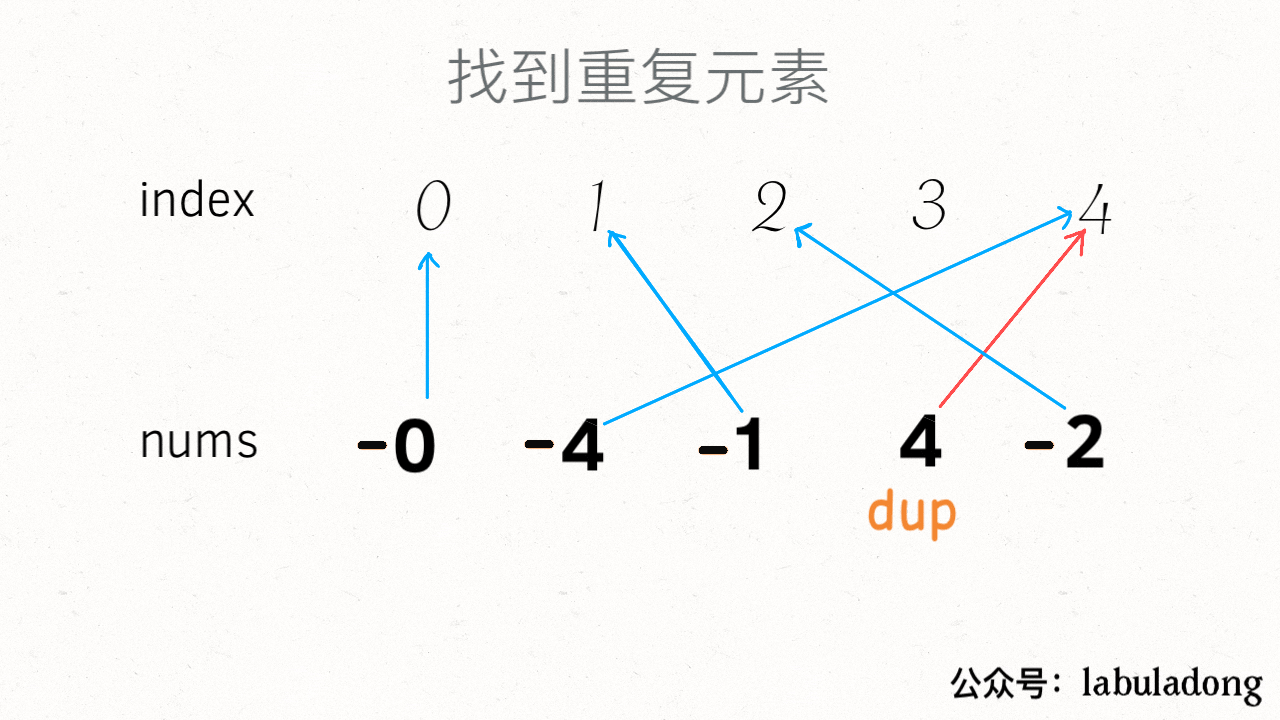
+
如果出现重复元素 `4`,直观结果就是,索引 `4` 所对应的元素已经是负数了:
-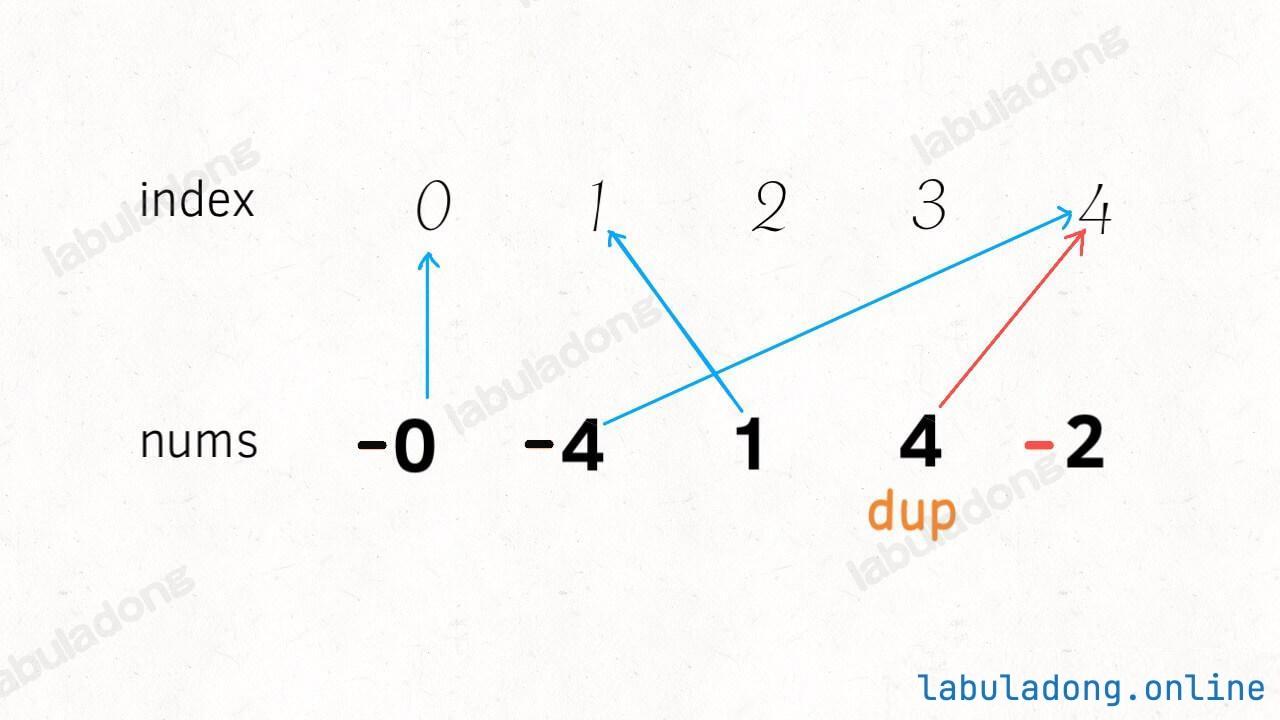
+
对于缺失元素 `3`,直观结果就是,索引 `3` 所对应的元素是正数:
-
+
对于这个现象,我们就可以翻译成代码了:
@@ -150,7 +150,7 @@ int[] findErrorNums(int[] nums) {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+
======其他语言代码======
diff --git "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/351円232円217円346円234円272円346円235円203円351円207円215円.md" "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/351円232円217円346円234円272円346円235円203円351円207円215円.md"
index cbd99a281c..ac13fc178e 100644
--- "a/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/351円232円217円346円234円272円346円235円203円351円207円215円.md"
+++ "b/351円253円230円351円242円221円351円235円242円350円257円225円347円263円273円345円210円227円/351円232円217円346円234円272円346円235円203円351円207円215円.md"
@@ -7,9 +7,9 @@
-
+
-**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。过年前最后一期打卡挑战即将开始,[点这里报名](https://aep.xet.tech/s/1a9ByX)。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
+**通知:[数据结构精品课](https://aep.h5.xeknow.com/s/1XJHEO) 已更新到 V2.1,[手把手刷二叉树系列课程](https://aep.xet.tech/s/3YGcq3) 上线。另外,建议你在我的 [网站](https://labuladong.github.io/algo/) 学习文章,体验更好。**
@@ -34,7 +34,7 @@
打完之后我就来发文了,因为我对游戏的匹配机制有了一点思考。
-
+
**所谓「隐藏分」我不知道是不是真的,毕竟匹配机制是所有竞技类游戏的核心环节,想必非常复杂,不是简单几个指标就能搞定的**。
@@ -48,7 +48,7 @@
力扣第 528 题「按权重随机选择」就是这样一个问题:
-
+
我们就来思考一下这个问题,解决按照权重随机选择元素的问题。
@@ -68,23 +68,23 @@
假设给你输入的权重数组是 `w = [1,3,2,1]`,我们想让概率符合权重,那么可以抽象一下,根据权重画出这么一条彩色的线段:
-
+
如果我在线段上面随机丢一个石子,石子落在哪个颜色上,我就选择该颜色对应的权重索引,那么每个索引被选中的概率是不是就是和权重相关联了?
**所以,你再仔细看看这条彩色的线段像什么?这不就是 [前缀和数组](https://labuladong.github.io/article/fname.html?fname=前缀和技巧) 嘛**:
-
+
那么接下来,如何模拟在线段上扔石子?
当然是随机数,比如上述前缀和数组 `preSum`,取值范围是 `[1, 7]`,那么我生成一个在这个区间的随机数 `target = 5`,就好像在这条线段中随机扔了一颗石子:
-
+
还有个问题,`preSum` 中并没有 5 这个元素,我们应该选择比 5 大的最小元素,也就是 6,即 `preSum` 数组的索引 3:
-
+
**如何快速寻找数组中大于等于目标值的最小元素?[二分搜索算法](https://labuladong.github.io/article/fname.html?fname=二分查找详解) 就是我们想要的**。
@@ -96,7 +96,7 @@
3、最后对这个索引减一(因为前缀和数组有一位索引偏移),就可以作为权重数组的索引,即最终答案:
-
+
### 解法代码
@@ -106,13 +106,13 @@
下面来抠细节,继续前面的例子:
-
+
就比如这个 `preSum` 数组,你觉得随机数 `target` 应该在什么范围取值?闭区间 `[0, 7]` 还是左闭右开 `[0, 7)`?
都不是,应该在闭区间 `[1, 7]` 中选择,**因为前缀和数组中 0 本质上是个占位符**,仔细体会一下:
-
+
所以要这样写代码:
@@ -223,4 +223,4 @@ class Solution {
**《labuladong 的算法小抄》已经出版,关注公众号查看详情;后台回复关键词「**进群**」可加入算法群;回复「**全家桶**」可下载配套 PDF 和刷题全家桶**:
-
+