diff --git a/docs/07_algorithm/07_01_enumeration_algorithm.md b/docs/07_algorithm/07_01_enumeration_algorithm.md index c0ccf69e..927f1e43 100644 --- a/docs/07_algorithm/07_01_enumeration_algorithm.md +++ b/docs/07_algorithm/07_01_enumeration_algorithm.md @@ -203,6 +203,14 @@ class Solution: - **时间复杂度**:$O(n^2)$。 - **空间复杂度**:$O(1)$。 +## 4. 总结 + +枚举算法通过遍历所有可能状态来寻找解,优点是实现简单、思路直接、正确性易于验证;缺点是在问题规模增大时时间开销迅速上升,往往无法满足效率要求。 + +它适用于规模较小、可快速验证答案的问题,或作为基线方案、结果校验与对拍工具。实战中应尽量结合剪枝(添加约束、提前判定不可能)、缩小搜索空间(利用对称性、边界与不变量)、降维与变量替换、以及避免重复计算等手段,显著提升效率。 + +实践建议是:先写出「能过的暴力正确解」,再围绕「减分支、减范围、减重算」迭代优化;当复杂度仍难以接受时,考虑切换到更合适的范式,例如哈希加速、双指针与滑动窗口、二分查找、分治、动态规划或图算法等。 + ## 练习题目 - [0001. 两数之和](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0001-0099/two-sum.md) diff --git a/docs/07_algorithm/07_02_recursive_algorithm.md b/docs/07_algorithm/07_02_recursive_algorithm.md index 050e9061..2f18770d 100644 --- a/docs/07_algorithm/07_02_recursive_algorithm.md +++ b/docs/07_algorithm/07_02_recursive_algorithm.md @@ -1,21 +1,23 @@ ## 1. 递归简介 -> **递归(Recursion)**:指的是一种通过重复将原问题分解为同类的子问题而解决的方法。在绝大数编程语言中,可以通过在函数中再次调用函数自身的方式来实现递归。 +> **递归(Recursion)**:是一种将复杂问题分解为与原问题结构相同的子问题,并通过重复求解这些子问题来获得最终解答的方法。在大多数编程语言中,递归通常通过函数自身的调用来实现。 -举个简单的例子来了解一下递归算法。比如阶乘的计算方法在数学上的定义为: +以阶乘为例,数学定义如下: $fact(n) = \begin{cases} 1 & \text{n = 0} \cr n \times fact(n - 1) & \text{n> 0} \end{cases}$ -根据阶乘计算方法的数学定义,我们可以使用调用函数自身的方式来实现阶乘函数 $fact(n)$ ,其实现代码可以写作: +我们可以直接用调用函数自身的方式实现阶乘函数 $fact(n),ドル代码如下: ```python def fact(n): + # 递归终止条件:当 n 等于 0 时,返回 1 if n == 0: return 1 + # 递归调用:n 乘以 fact(n - 1),将问题规模缩小 return n * fact(n - 1) ``` -以 $n = 6$ 为例,上述代码中阶乘函数 $fact(6)$ 的计算过程如下: +以 $n = 6$ 为例,阶乘函数 $fact(6)$ 的递归计算步骤如下: ```python fact(6) @@ -34,116 +36,91 @@ fact(6) = 720 ``` -上面的例子也可以用语言描述为: +上述例子可以用如下方式描述递归的执行过程: -1. 函数从 $fact(6)$ 开始,一层层地调用 $fact(5)$、$fact(4)$、...... 一直调用到最底层的 $fact(0)$。 -2. 当 $n == 0$ 时,$fact(0)$ 不再继续调用自身,而是直接向上一层返回结果 1ドル$。 -3. $fact(1)$ 通过下一层 $fact(0)$ 的计算结果得出 $fact(1) = 1 \times 1 = 1,ドル从而向上一层返回结果 1ドル$。 -4. $fact(2)$ 通过下一层 $fact(1)$ 的计算结果得出 $fact(2) = 2 \times 1 = 2 ,ドル从而向上一层返回结果 2ドル$。 -5. $fact(3)$ 通过下一层 $fact(2)$ 的计算结果得出 $fact(3) = 3 \times 2 = 6 ,ドル从而向上一层返回结果 6ドル$。 -6. $fact(4)$ 通过下一层 $fact(3)$ 的计算结果得出 $fact(4) = 4 \times 6 = 24,ドル从而向上一层返回结果 24ドル$。 -7. $fact(5)$ 通过下一层 $fact(4)$ 的计算结果得出 $fact(5) = 5 \times 24 = 120,ドル从而向上一层返回结果 120ドル$。 -8. $fact(6)$ 通过下一层 $fact(5)$ 的计算结果得出 $fact(6) = 6 \times 120 = 720,ドル从而返回函数的最终结果 720ドル$。 +1. 从 $fact(6)$ 开始,函数不断递归调用自身,依次进入 $fact(5)$、$fact(4)$、......,直到到达最底层的 $fact(0)$。 +2. 当 $n == 0$ 时,$fact(0)$ 满足终止条件,直接返回 1ドル,ドル递归不再继续向下。 +3. 返回阶段,从 $fact(0)$ 开始逐层向上,每一层利用下一层的返回值进行计算: + - $fact(1)$:通过 $fact(0)$ 的结果 1ドル,ドル计算 $fact(1) = 1 \times 1 = 1,ドル返回 1ドル$。 + - $fact(2)$:通过 $fact(1)$ 的结果 1ドル,ドル计算 $fact(2) = 2 \times 1 = 2,ドル返回 2ドル$。 + - $fact(3)$:通过 $fact(2)$ 的结果 2ドル,ドル计算 $fact(3) = 3 \times 2 = 6,ドル返回 6ドル$。 + - $fact(4)$:通过 $fact(3)$ 的结果 6ドル,ドル计算 $fact(4) = 4 \times 6 = 24,ドル返回 24ドル$。 + - $fact(5)$:通过 $fact(4)$ 的结果 24ドル,ドル计算 $fact(5) = 5 \times 24 = 120,ドル返回 120ドル$。 + - $fact(6)$:通过 $fact(5)$ 的结果 120ドル,ドル计算 $fact(6) = 6 \times 120 = 720,ドル最终返回 720ドル$。 -这就是阶乘函数的递归计算过程。 +整个递归过程分为两步: -根据上面的描述,我们可以把阶乘函数的递归计算过程分为两个部分: +1. 向下递推:不断分解问题,直到满足终止条件($n == 0$)。 +2. 向上回归:逐层返回结果,最终得到原问题的解(即返回 $fact(6) == 720$)。 -1. 先逐层向下调用自身,直到达到结束条件(即 $n == 0$)。 -2. 然后再向上逐层返回结果,直到返回原问题的解(即返回 $fact(6) == 720$)。 - -这两个部分也可以叫做「递推过程」和「回归过程」,如下面两幅图所示: +如下图所示: ![递推过程](https://qcdn.itcharge.cn/images/20220407160648.png) ![回归过程](https://qcdn.itcharge.cn/images/20220407160659.png) -如上面所说,我们可以把「递归」分为两个部分:「递推过程」和「回归过程」。 - -- **递推过程**:指的是将原问题一层一层地分解为与原问题形式相同、规模更小的子问题,直到达到结束条件时停止,此时返回最底层子问题的解。 -- **回归过程**:指的是从最底层子问题的解开始,逆向逐一回归,最终达到递推开始时的原问题,返回原问题的解。 - -「递推过程」和「回归过程」是递归算法的精髓。从这个角度来理解递归,递归的基本思想就是: **把规模大的问题不断分解为子问题来解决。** +简而言之,递归包含「递推过程」和「回归过程」: -同时,因为解决原问题和不同规模的小问题往往使用的是相同的方法,所以就产生了函数调用函数自身的情况,这也是递归的定义所在。 +- **递推过程**:将大问题逐步分解为更小的同类子问题,直到终止条件。 +- **回归过程**:从最小子问题开始,逐层返回结果,最终解决原问题。 -## 2. 递归和数学归纳法 +递归的核心思想就是:**把大问题拆解为小问题,逐步解决。** 因为每一层的处理方式相同,所以递归函数会调用自身,这正是递归的本质。 -递归的数学模型其实就是「数学归纳法」。这里简单复习一下数学归纳法的证明步骤: +## 2. 递归与数学归纳法 -1. 证明当 $n = b$ ($b$ 为基本情况,通常为 0ドル$ 或者 1ドル$)时,命题成立。 -2. 证明当 $n> b$ 时,假设 $n = k$ 时命题成立,那么可以推导出 $n = k + 1$ 时命题成立。这一步不是直接证明的,而是先假设 $n = k$ 时命题成立,利用这个条件,可以推论出 $n = k + 1$ 时命题成立。 +递归的本质与「数学归纳法」高度契合。我们先简要回顾数学归纳法的基本步骤: -通过以上两步证明,就可以说:当 $n>= b$ 时,命题都成立。 +1. **基础情形**:证明当 $n = b$($b$ 通常为 0ドル$ 或 1ドル$)时,命题成立。 +2. **归纳步骤**:假设当 $n = k$ 时命题成立,进一步证明 $n = k + 1$ 时命题也成立。这里的关键是利用 $n = k$ 成立的假设,推导出 $n = k + 1$ 也成立。 -我们可以从「数学归纳法」的角度来解释递归: +完成上述两步后,即可得出:对于所有 $n \ge b,ドル命题均成立。 -- **递归终止条件**:数学归纳法第一步中的 $n = b,ドル可以直接得出结果。 -- **递推过程**:数学归纳法第二步中的假设部分(假设 $n = k$ 时命题成立),也就是假设我们当前已经知道了 $n = k$ 时的计算结果。 -- **回归过程**:数学归纳法第二步中的推论部分(根据 $n = k$ 推论出 $n = k + 1$),也就是根据下一层的结果,计算出上一层的结果。 +将递归与数学归纳法对应起来,可以这样理解: -事实上,数学归纳法的思考过程也正是在解决某些数列问题时,可以使用递归算法的原因。比如阶乘、数组前 $n$ 项和、斐波那契数列等等。 +- **递归终止条件**:对应于数学归纳法的基础情形($n = b$),此时直接给出结果。 +- **递推过程**:对应于归纳假设部分(假设 $n = k$ 时成立),即假设我们已经知道了规模更小的问题的解。 +- **回归过程**:对应于归纳推导部分(由 $n = k$ 推出 $n = k + 1$),即利用子问题的解,推导出当前问题的解。 -## 3. 递归三步走 +正因为数学归纳法的推理方式与递归的分解和回归过程一致,所以在解决如阶乘、前 $n$ 项和、斐波那契数列等问题时,递归算法往往是最自然的选择。 -上面我们提到,递归的基本思想就是: **把规模大的问题不断分解为子问题来解决。** 那么,在写递归的时候,我们可以按照这个思想来书写递归,具体步骤如下: +## 3. 递归三步法 -1. **写出递推公式**:找到将原问题分解为子问题的规律,并且根据规律写出递推公式。 -2. **明确终止条件**:推敲出递归的终止条件,以及递归终止时的处理方法。 -3. **将递推公式和终止条件翻译成代码**: - 1. 定义递归函数(明确函数意义、传入参数、返回结果等)。 - 2. 书写递归主体(提取重复的逻辑,缩小问题规模)。 - 3. 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 +递归的核心思想是:**把大问题拆解为小问题,逐步解决**。写递归时,可以遵循以下三步: -### 3.1 写出递推公式 +1. **写递推公式**:找出原问题与子问题的关系,写出递推公式。 +2. **确定终止条件**:明确递归何时结束,以及结束时的返回值。 +3. **翻译为代码**: + - 定义递归函数(明确参数和返回值含义) + - 编写递归主体(递推公式对应的递归调用) + - 加入终止条件的判断和处理 -写出递推公式的关键在于:**找到将原问题分解为子问题的规律,并将其抽象成递推公式**。 +### 3.1 写递推公式 -我们在思考递归的逻辑时,没有必要在大脑中将整个递推过程和回归过程一层层地想透彻。很可能还没有递推到栈底呢,脑子就已经先绕晕了。 +递归的关键在于:将原问题拆解为更小、结构相同的子问题,并用递推公式加以表达。例如,阶乘问题的递推公式为 $fact(n) = n \times fact(n - 1)$。 -之前讲解的阶乘例子中,一个问题只需要分解为一个子问题,我们很容易能够想清楚「递推过程」和「回归过程」的每一个步骤,所以写起来和理解起来都不难。 +在思考递归时,无需把每一层的递推和回归过程都在脑海中推演到底,否则容易陷入细节而感到困惑。以阶乘为例,它只需分解为一个子问题,因此递归的每一步都容易理解和实现。 -但是当我们面对的是一个问题需要分解为多个子问题的情况时,就没有那么容易想清楚「递推过程」和「回归过程」的每一个步骤了。 +但当一个问题需要分解为多个子问题时,逐层推演每一步的递推和回归过程就会变得复杂且难以理清。 -那么我们应该如何思考「递推过程」和「回归过程」呢,又该如何写出递归中的递推公式呢? +此时,推荐的思考方式是:假设所有子问题(如 $B$、$C$、$D$)都已经解决,我们只需思考如何利用这些子问题的解来解决原问题 $A$。无需再深入每个子问题的内部递归细节,这样可以大大简化思考难度。 -如果一个问题 $A,ドル可以分解为若干个规模较小、与原问题形式相同的子问题 $B$、$C$、$D,ドル那么这些子问题就可以用相同的解题思路来解决。我们可以假设 $B$、$C$、$D$ 已经解决了,然后只需要考虑在这个基础上去思考如何解决问题 $A$ 即可。不需要再一层层往下思考子问题与子子问题、子子问题与子子子问题之间的关系。这样理解起来就简单多了。 +实际上,从原问题 $A$ 拆解为子问题 $B$、$C$、$D$ 的过程,就是递归的「递推过程」;而将子问题的解合并为原问题的解,则是「回归过程」。只要明确了如何划分子问题,以及如何通过子问题的解来解决原问题,就能顺利写出递推公式。 -从问题 $A$ 到分解为子问题 $B$、$C$、$D$ 的思考过程其实就是递归的「递推过程」。而从子问题 $B$、$C$、$D$ 的解回到问题 $A$ 的解的思考过程其实就是递归的「回归过程」。想清楚了「如何划分子问题」和「如何通过子问题来解决原问题」这两个过程,也就想清楚了递归的「递推过程」和「回归过程」。 - -然后,我们只需要考虑原问题与子问题之间的关系,就能够在此基础上,写出递推公式了。 +因此,编写递归时,重点关注原问题与子问题之间的关系,并据此写出递推公式即可。 ### 3.2 明确终止条件 -递归的终止条件也叫做递归出口。在写出了递推公式之后,就要考虑递归的终止条件是什么。如果没有递归的终止条件,函数就会无限地递归下去,程序就会失控崩溃了。通常情况下,递归的终止条件是问题的边界值。 - -在找到递归的终止条件时,我们应该直接给出该条件下的处理方法。一般地,在这种情境下,问题的解决方案是直观的、容易的。例如阶乘中 $fact(0) = 1$。斐波那契数列中 $f(1) = 1,ドル$f(2) = 2$。 - -### 3.3 将递推公式和终止条件翻译成代码 - -在写出递推公式和明确终止条件之后,我们就可以将其翻译成代码了。这一步也可以分为 3ドル$ 步来做: - -1. **定义递归函数**:明确函数意义、传入参数、返回结果等。 -2. **书写递归主体**:提取重复的逻辑,缩小问题规模。 -3. **明确递归终止条件**:给出递归终止条件,以及递归终止时的处理方法。 - -#### 3.3.1 定义递归函数 - -在定义递归函数时,一定要明确递归函数的意义,也就是要明白这个问题传入的参数是什么,最终返回的结果是要解决的什么问题。 - -比如说阶乘函数 $fact(n),ドル这个函数的传入参数是问题的规模 $n,ドル最终返回的结果是 $n$ 的阶乘值。 +递归必须有终止条件(递归出口),否则会无限递归导致程序崩溃。终止条件通常是问题的边界值,并在此时直接给出答案。例如,$fact(0) = 1,ドル$f(1) = 1$。 -#### 3.3.2 书写递归主体 +### 3.3 翻译为代码 -在将原问题划分为子问题,并根据原问题和子问题的关系,我们就可以推论出对应的递推公式。然后根据递推公式,就可以将其转换为递归的主体代码。 +将递推公式和终止条件转化为代码,通常分为三步: -#### 3.3.3 明确递归终止条件 +1. **定义递归函数**:明确参数和返回值的含义。 +2. **编写递归主体**:根据递推公式递归调用自身。 +3. **加入终止条件**:用条件语句判断并处理终止情况。 -这一步其实就是将「3.2 明确终止条件」章节中的递归终止条件和终止条件下的处理方法转换为代码中的条件语句和对应的执行语句。 - -#### 3.3.4 递归伪代码 - -根据上述递归书写的步骤,我们就可以写出递归算法的代码了。递归算法的伪代码如下: +综合上述步骤,递归伪代码如下: ```python def recursion(大规模问题): @@ -153,37 +130,37 @@ def recursion(大规模问题): return recursion(小规模问题) ``` -## 4. 递归的注意点 +## 4. 递归的注意事项 ### 4.1 避免栈溢出 -在程序执行中,递归是利用堆栈来实现的。每一次递推都需要一个栈空间来保存调用记录,每当进入一次函数调用,栈空间就会加一层栈帧。每一次回归,栈空间就会减一层栈帧。由于系统中的栈空间大小不是无限的,所以,如果递归调用的次数过多,会导致栈空间溢出。 - -为了避免栈溢出,我们可以在代码中限制递归调用的最大深度来解决问题。当递归调用超过一定深度时(比如 100)之后,不再进行递归,而是直接返回报错。 +递归在程序执行时依赖于调用栈。每递归调用一次,系统会为该调用分配一个新的栈帧;每当递归返回时,栈帧被销毁。由于系统栈空间有限,如果递归层数过深,极易导致栈溢出(Stack Overflow)。 -当然这种做法并不能完全避免栈溢出,也无法完全解决问题,因为系统允许的最大递归深度跟当前剩余的占空间有关,事先无法计算。 +为降低栈溢出的风险,可以在代码中人为设置递归的最大深度(如 100 层),超过后直接返回错误或采取其他处理措施。但这种方式并不能彻底杜绝栈溢出,因为系统允许的最大递归深度受限于当前可用栈空间,且难以精确预估。 -如果使用递归算法实在无法解决问题,我们可以考虑将递归算法变为非递归算法(即递推算法)来解决栈溢出的问题。 +如果递归深度不可控或递归算法难以避免栈溢出,建议将递归改写为非递归(迭代)算法,即用循环和显式栈模拟递归过程,从根本上解决栈空间受限的问题。 ### 4.2 避免重复运算 -在使用递归算法时,还可能会出现重复运算的问题。 +递归算法常常会遇到重复计算的问题,尤其是在分治结构中多个子问题重叠时。例如,斐波那契数列的递归定义如下: -比如斐波那契数列的定义是: +$$ +f(n) = \begin{cases} +0 & n = 0 \\ +1 & n = 1 \\ +f(n-1) + f(n-2) & n> 1 +\end{cases} +$$ -$f(n) = \begin{cases} 0 & n = 0 \cr 1 & n = 1 \cr f(n - 2) + f(n - 1) & n> 1 \end{cases}$ - -其对应的递归过程如下图所示: +如下图所示,计算 $f(5)$ 时,$f(3)$ 会被多次递归计算,$f(2)$、$f(1)$、$f(0)$ 也会被重复计算,导致效率极低。 ![斐波那契数列的递归过程](https://qcdn.itcharge.cn/images/20230307164107.png) -从图中可以看出:想要计算 $f(5),ドル需要先计算 $f(3)$ 和 $f(4),ドル而在计算 $f(4)$ 时还需要计算 $f(3),ドル这样 $f(3)$ 就进行了多次计算。同理 $f(0)$、$f(1)$、$f(2)$ 都进行了多次计算,就导致了重复计算问题。 - -为了避免重复计算,我们可以使用一个缓存(哈希表、集合或数组)来保存已经求解过的 $f(k)$ 的结果,这也是动态规划算法中的做法。当递归调用用到 $f(k)$ 时,先查看一下之前是否已经计算过结果,如果已经计算过,则直接从缓存中取值返回,而不用再递推下去,这样就避免了重复计算问题。 +为避免重复运算,可以引入缓存机制(如哈希表、数组或集合)记录已经计算过的子问题结果。这种做法称为「记忆化递归」或「递归 + 备忘录」,也是动态规划的核心思想之一。每次递归调用前,先检查缓存中是否已有结果,若有则直接返回,无需再次递归,从而显著提升效率。 ## 5. 递归的应用 -### 5.1 斐波那契数 +### 5.1 经典例题:斐波那契数 #### 5.1.1 题目链接 @@ -224,16 +201,17 @@ $f(n) = \begin{cases} 0 & n = 0 \cr 1 & n = 1 \cr f(n - 2) + f(n - 1) & n> 1 \e ##### 思路 1:递归算法 -根据我们的递推三步走策略,写出对应的递归代码。 +按照递归解题的「三步走」策略,可以将斐波那契数列问题的递归实现过程梳理如下: + +1. 写递推公式:$f(n) = f(n - 1) + f(n - 2)$。 +2. 确定终止条件:$f(0) = 0,ドル$f(1) = 1$。 +3. 翻译为代码: + 1. 定义递归函数 `fib(self, n)`,其中 $n$ 表示问题规模,返回第 $n$ 个斐波那契数。 + 2. 递归主体为:`return self.fib(n - 1) + self.fib(n - 2)`。 + 3. 递归终止条件: + - `if n == 0: return 0` + - `if n == 1: return 1` -1. 写出递推公式:$f(n) = f(n - 1) + f(n - 2)$。 -2. 明确终止条件:$f(0) = 0, f(1) = 1$。 -3. 翻译为递归代码: - 1. 定义递归函数:`fib(self, n)` 表示输入参数为问题的规模 $n,ドル返回结果为第 $n$ 个斐波那契数。 - 2. 书写递归主体:`return self.fib(n - 1) + self.fib(n - 2)`。 - 3. 明确递归终止条件: - 1. `if n == 0: return 0` - 2. `if n == 1: return 1` ##### 思路 1:代码 @@ -252,7 +230,7 @@ class Solution: - **时间复杂度**:$O((\frac{1 + \sqrt{5}}{2})^n)$。具体证明方法参考 [递归求斐波那契数列的时间复杂度,不要被网上的答案误导了 - 知乎](https://zhuanlan.zhihu.com/p/256344121)。 - **空间复杂度**:$O(n)$。每次递归的空间复杂度是 $O(1),ドル 调用栈的深度为 $n,ドル所以总的空间复杂度就是 $O(n)$。 -### 5.2 二叉树的最大深度 +### 5.2 经典例题:二叉树的最大深度 #### 5.2.1 题目链接 @@ -289,15 +267,15 @@ class Solution: ##### 思路 1: 递归算法 -根据递归三步走策略,写出对应的递归代码。 +按照递归解题的「三步走」策略,整理递归解法如下: -1. 写出递推公式:**当前二叉树的最大深度 = max(当前二叉树左子树的最大深度, 当前二叉树右子树的最大深度) + 1**。 - - 即:先得到左右子树的高度,在计算当前节点的高度。 -2. 明确终止条件:当前二叉树为空。 -3. 翻译为递归代码: - 1. 定义递归函数:`maxDepth(self, root)` 表示输入参数为二叉树的根节点 $root,ドル返回结果为该二叉树的最大深度。 - 2. 书写递归主体:`return max(self.maxDepth(root.left) + self.maxDepth(root.right))`。 - 3. 明确递归终止条件:`if not root: return 0` +1. 写递推公式:**当前二叉树的最大深度 = max(左子树最大深度, 右子树最大深度) + 1**。 + - 即:递归分别计算左右子树的深度,取较大值后加 1,得到当前节点的深度。 +2. 确定终止条件:当当前节点为空(即 root 为 None)时,返回 0。 +3. 翻译为代码: + 1. 定义递归函数:`maxDepth(self, root)`,参数为二叉树根节点 $root,ドル返回该树的最大深度。 + 2. 递归主体:`return max(self.maxDepth(root.left), self.maxDepth(root.right)) + 1`。 + 3. 终止条件判断:`if not root: return 0`。 ##### 思路 1:代码 @@ -315,6 +293,16 @@ class Solution: - **时间复杂度**:$O(n),ドル其中 $n$ 是二叉树的节点数目。 - **空间复杂度**:$O(n)$。递归函数需要用到栈空间,栈空间取决于递归深度,最坏情况下递归深度为 $n,ドル所以空间复杂度为 $O(n)$。 +## 6. 总结 + +递归的本质是将大问题拆成同结构的小问题,先「递推」到底,再「回归」向上合并结果。写递归时只需站在当前层思考:如果更小规模的子问题都已解决,我如何用它们的结果得到当前答案。 + +它与数学归纳法一一对应:终止条件对应基础情形,递推与回归对应「假设成立 → 推出更大规模成立」。因此,实践上先写清递推关系,再补充明确的递归出口,最后把思路直接翻译成代码即可。 + +实战中要特别注意两点:其一,递归层数过深可能导致栈溢出,可限制深度或改写为迭代;其二,子问题重叠会造成重复计算,可使用记忆化(缓存)或转为自底向上的动态规划来优化。 + +递归尤其适合链式、树形与分治类问题,如二叉树深度、DFS 等。建议先保证正确性,再视场景用缓存或迭代 / DP手段优化时间与空间开销。 + ## 练习题目 - [0509. 斐波那契数](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0500-0599/fibonacci-number.md) diff --git a/docs/07_algorithm/07_03_divide_and_conquer_algorithm.md b/docs/07_algorithm/07_03_divide_and_conquer_algorithm.md index fb1d8b90..c68c5a4e 100644 --- a/docs/07_algorithm/07_03_divide_and_conquer_algorithm.md +++ b/docs/07_algorithm/07_03_divide_and_conquer_algorithm.md @@ -2,121 +2,148 @@ ### 1.1 分治算法的定义 -> **分治算法(Divide and Conquer)**:字面上的解释是「分而治之」,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。 +> **分治算法(Divide and Conquer)**:即「分而治之」,把一个复杂问题拆分成多个相同或相似的子问题,递归分解,直到子问题足够简单可以直接解决,最后将子问题的解合并得到原问题的解。 -简单来说,分治算法的基本思想就是: **把规模大的问题不断分解为子问题,使得问题规模减小到可以直接求解为止。** +简而言之,分治算法就是:**把大问题不断拆小,直到可以直接求解,再合并结果**。 ![分治算法的基本思想](https://qcdn.itcharge.cn/images/20220413153059.png) -### 1.2 分治算法和递归算法的异同 +### 1.2 分治算法与递归算法的关系 -从定义上来看,分治算法的思想和递归算法的思想是一样的,都是把规模大的问题不断分解为子问题。 +分治和递归都强调「拆分问题」。递归是一种实现方式,分治是一种思想。可以理解为:$\text{递归算法} \subset \text{分治算法}$。 -其实,分治算法和递归算法的关系是包含与被包含的关系,可以看做: $\text{递归算法} \in \text{分治算法}$。 - -分治算法从实现方式上来划分,可以分为两种:「递归算法」和「迭代算法」。 +分治算法常用递归实现,也可以用迭代实现。例如:快速傅里叶变换、二分查找、非递归归并排序等。 ![分治算法的实现方式](https://qcdn.itcharge.cn/images/20240513162133.png) -一般情况下,分治算法比较适合使用递归算法来实现。但除了递归算法之外,分治算法还可以通过迭代算法来实现。比较常见的例子有:快速傅里叶变换算法、二分查找算法、非递归实现的归并排序算法等等。 - -我们先来讲解一下分支算法的适用条件,再来讲解一下基本步骤。 +下面先介绍分治算法的适用条件,再讲基本步骤。 ### 1.3 分治算法的适用条件 -分治算法能够解决的问题,一般需要满足以下 4ドル$ 个条件: +分治算法适用于满足以下 4 个条件的问题: -1. **可分解**:原问题可以分解为若干个规模较小的相同子问题。 -2. **子问题可独立求解**:分解出来的子问题可以独立求解,即子问题之间不包含公共的子子问题。 -3. **具有分解的终止条件**:当问题的规模足够小时,能够用较简单的方法解决。 -4. **可合并**:子问题的解可以合并为原问题的解,并且合并操作的复杂度不能太高,否则就无法起到减少算法总体复杂度的效果了。 +1. **可分解**:原问题能拆分为若干规模更小、结构相同的子问题。 +2. **子问题独立**:各子问题互不影响,无重叠部分。 +3. **有终止条件**:子问题足够小时可直接解决。 +4. **可合并**:子问题的解能高效合并为原问题的解,且合并过程不能太复杂。 ## 2. 分治算法的基本步骤 -使用分治算法解决问题主要分为 3ドル$ 个步骤: +分治算法通常包括以下三个核心步骤: -1. **分解**:把要解决的问题分解为成若干个规模较小、相对独立、与原问题形式相同的子问题。 -2. **求解**:递归求解各个子问题。 -3. **合并**:按照原问题的要求,将子问题的解逐层合并构成原问题的解。 +1. **分解**:将原问题拆分为若干个规模更小、结构相同且相互独立的子问题。 +2. **求解**:递归地解决每个子问题。 +3. **合并**:将各子问题的解按照原问题的要求逐层合并,最终得到整体问题的解。 -其中第 1ドル$ 步中将问题分解为若干个子问题时,最好使子问题的规模大致相同。换句话说,将一个问题分成大小相等的 $k$ 个子问题的处理方法是行之有效的。在许多问题中,可以取 $k = 2$。这种使子问题规模大致相等的做法是出自一种平衡子问题的思想,它几乎总是比子问题规模不等的做法要好。 +在第 1ドル$ 步分解时,建议将问题划分为规模尽量相等的 $k$ 个子问题,这样可以保持递归树的平衡,提升算法效率。实际应用中,$k = 2$ 是最常见的选择。子问题规模均衡,通常比不均衡的划分方式更优。 -其中第 2ドル$ 步的「递归求解各个子问题」指的是按照同样的分治策略进行求解,即通过将这些子问题分解为更小的子子问题来进行求解。就这样一直分解下去,直到分解出来的子问题简单到只用常数操作时间即可解决为止。 +第 2ドル$ 步的递归求解,意味着对子问题继续应用相同的分治策略,直到子问题足够简单,可以直接用常数时间解决为止。 -在完成第 2ドル$ 步之后,最小子问题的解可用常数时间求得。然后我们再按照递归算法中回归过程的顺序,由底至上地将子问题的解合并起来,逐级上推就构成了原问题的解。 +完成递归求解后,最小子问题的解可直接获得。随后,按照递归回归的顺序,自底向上逐步合并子问题的解,最终得到原问题的答案。 -按照分而治之的策略,在编写分治算法的代码时,也是按照上面的 3ドル$ 个步骤来编写的,其对应的伪代码如下: +在实际编写分治算法时,代码结构也应严格遵循上述 3ドル$ 个步骤,便于理解和维护。伪代码如下: ```python -def divide_and_conquer(problems_n): # problems_n 为问题规模 - if problems_n < d: # 当问题规模足够小时,直接解决该问题 - return solove() # 直接求解 - - problems_k = divide(problems_n) # 将问题分解为 k 个相同形式的子问题 - - res = [0 for _ in range(k)] # res 用来保存 k 个子问题的解 - for problem_k in problems_k: - res[i] = divide_and_conquer(problem_k) # 递归的求解 k 个子问题 - - ans = merge(res) # 合并 k 个子问题的解 - return ans # 返回原问题的解 +def divide_and_conquer(problem_n): + """ + 分治算法通用模板 + :param problem_n: 问题规模 + :return: 原问题的解 + """ + # 1. 递归终止条件:当问题规模足够小时,直接解决 + if problem_n < d: # d 为可直接求解的最小规模 + return solve(problem_n) # 直接求解(注意:原代码有拼写错误,应为 solve) + + # 2. 分解:将原问题分解为 k 个子问题 + problems_k = divide(problem_n) # divide 函数返回 k 个子问题的列表 + + # 3. 递归求解每个子问题 + res = [] + for sub_problem in problems_k: + sub_res = divide_and_conquer(sub_problem) # 递归求解子问题 + res.append(sub_res) # 收集每个子问题的解 + + # 4. 合并:将 k 个子问题的解合并为原问题的解 + ans = merge(res) + return ans # 返回原问题的解 ``` -## 3. 分治算法的复杂度分析 - - 分治算法中,在不断递归后,最后的子问题将变得极为简单,可在常数操作时间内予以解决,其带来的时间复杂度在整个分治算法中的比重微乎其微,可以忽略不计。所以,分治算法的时间复杂度实际上是由「分解」和「合并」两个部分构成的。 - -一般来讲,分治算法将一个问题划分为 $a$ 个形式相同的子问题,每个子问题的规模为 $n/b,ドル则总的时间复杂度的递归表达式可以表示为: +## 3. 分治算法分析 -$T(n) = \begin{cases} \Theta{(1)} & n = 1 \cr a \times T(n/b) + f(n) & n> 1 \end{cases}$ +分治算法的核心在于:将大问题递归拆分为更小的子问题,直到子问题足够简单(通常可直接用常数时间解决),然后合并子问题的解。实际的时间复杂度主要由「分解」和「合并」两个过程决定。 -其中,每次分解时产生的子问题个数是 $a$ ,每个子问题的规模是原问题规模的 1ドル / b,ドル分解和合并 $a$ 个子问题的时间复杂度是 $f(n)$。 +一般情况下,分治算法会把原问题拆成 $a$ 个规模为 $n/b$ 的子问题,递归式为: -这样,求解一个分治算法的时间复杂度,就是求解上述递归表达式。关于递归表达式的求解有多种方法,这里我们介绍一下比较常用的「递推求解法」和「递归树法」。 +$$ +T(n) = +\begin{cases} +\Theta(1) & n = 1 \\ +a \times T(n/b) + f(n) & n> 1 +\end{cases} +$$ -### 3.1 递推求解法 +其中,$a$ 表示子问题个数,$n/b$ 是每个子问题的规模,$f(n)$ 是分解和合并的总耗时。 -根据问题的递归表达式,通过一步步递推分解推导,从而得到最终结果。 +求解分治算法复杂度,常用两种方法:递推法和递归树法。 -以「归并排序算法」为例,接下来我们通过递推求解法计算一下归并排序算法的时间复杂度。 +### 3.1 递推法 -我们得出归并排序算法的递归表达式如下: +以归并排序为例,其递归式为: -$T(n) = \begin{cases} O{(1)} & n = 1 \cr 2 \times T(n/2) + O(n) & n> 1 \end{cases}$ +$$ +T(n) = +\begin{cases} +O(1) & n = 1 \\ +2T(n/2) + O(n) & n> 1 +\end{cases} +$$ -根据归并排序的递归表达式,当 $n> 1$ 时,可以递推求解: +递推展开如下: -$$\begin{aligned} T(n) & = 2 \times T(n/2) + O(n) \cr & = 2 \times (2 \times T(n / 4) + O(n/2)) + O(n) \cr & = 4 \times T(n/4) + 2 \times O(n) \cr & = 8 \times T(n/8) + 3 \times O(n) \cr & = ...... \cr & = 2^x \times T(n/2^x) + x \times O(n) \end{aligned}$$ +$$ +\begin{aligned} +T(n) &= 2T(n/2) + O(n) \\ + &= 2[2T(n/4) + O(n/2)] + O(n) \\ + &= 4T(n/4) + 2O(n/2) + O(n) \\ + &= 4T(n/4) + O(n) + O(n) \\ + &= 8T(n/8) + 3O(n) \\ + &\dots \\ + &= 2^x T(n/2^x) + xO(n) +\end{aligned} +$$ -递推最终规模为 1ドル,ドル令 $n = 2^x,ドル则 $x = \log_2n,ドル则: +当 $n = 2^x,ドル$x = \log_2 n,ドル最终: -$$\begin{aligned} T(n) & = n \times T(1) + \log_2n \times O(n) \cr & = n + \log_2n \times O(n) \cr & = O(n \times \log_2n) \end{aligned}$$ +$$ +T(n) = n \cdot T(1) + \log_2 n \cdot O(n) = O(n \log n) +$$ -则归并排序的时间复杂度为 $O(n \times \log_2n)$。 +则归并排序的时间复杂度为 $O(n \log n)$。 ### 3.2 递归树法 -递归树求解方式其实和递推求解一样,只不过递归树能够更清楚直观的显示出来,更能够形象地表达每层分解的节点和每层产生的时间成本。 +递归树法可以直观展示每层的分解和合并成本。以归并排序为例: -使用递归树法计算时间复杂度的公式为: +- 每层分解为 2 个子问题,总共 $\log_2 n$ 层。 +- 每层合并的总耗时为 $O(n)$。 -$\text{时间复杂度} = \text{叶子数} \times T(1) + \text{成本和} = 2^x \times T(1) + x \times O(n)$。 +总复杂度为: -我们还是以「归并排序算法」为例,通过递归树法计算一下归并排序算法的时间复杂度。 +$$ +\begin{aligned} +\text{总耗时} &= \underbrace{n \cdot O(1)}_{\text{叶子节点}} + \underbrace{O(n) \cdot \log_2 n}_{\text{每层合并}} \\ + &= O(n) + O(n \log n) \\ + &= O(n \log n) +\end{aligned} +$$ -归并排序算法的递归表达式如下: - -$T(n) = \begin{cases} O{(1)} & n = 1 \cr 2T(n/2) + O(n) & n> 1 \end{cases}$ - -其对应的递归树如下图所示。 +下图为归并排序的递归树示意: ![归并排序算法的递归树](https://qcdn.itcharge.cn/images/20220414171458.png) -因为 $n = 2^x,ドル则 $x = \log_2n,ドル则归并排序算法的时间复杂度为:2ドル^x \times T(1) + x \times O(n) = n + \log_2n \times O(n) = O(n \times \log_2n)$。 - ## 4. 分治算法的应用 -### 4.1 归并排序 +### 4.1 经典例题:归并排序 #### 4.1.1 题目链接 @@ -142,13 +169,13 @@ $T(n) = \begin{cases} O{(1)} & n = 1 \cr 2T(n/2) + O(n) & n> 1 \end{cases}$ #### 4.1.3 解题思路 -我们使用归并排序算法来解决这道题。 +本题采用归并排序算法求解,其步骤如下: -1. **分解**:将待排序序列中的 $n$ 个元素分解为左右两个各包含 $\frac{n}{2}$ 个元素的子序列。 -2. **求解**:递归将子序列进行分解和排序,直到所有子序列长度为 1ドル$。 -3. **合并**:把当前序列组中有序子序列逐层向上,进行两两合并。 +1. **分解**:将待排序数组递归地一分为二,分别划分为左右两个子数组,每个子数组大致包含 $\frac{n}{2}$ 个元素。 +2. **递归排序**:对左右两个子数组分别递归进行归并排序,直到子数组长度为 1ドル,ドル此时视为有序。 +3. **合并**:将两个有序子数组合并为一个有序数组,逐层向上合并,最终得到整体有序的结果。 -使用归并排序算法对数组排序的过程如下图所示。 +下图展示了归并排序对数组排序的具体过程: ![归并排序算法对数组排序的过程](https://qcdn.itcharge.cn/images/20220414204405.png) @@ -183,7 +210,7 @@ class Solution: return self.mergeSort(nums) ``` -### 4.2 二分查找 +### 4.2 经典例题:二分查找 #### 4.2.1 题目链接 @@ -211,15 +238,17 @@ class Solution: #### 4.2.3 解题思路 -我们使用分治算法来解决这道题。与其他分治题目不一样的地方是二分查找不用进行合并过程,最小子问题的解就是原问题的解。 +本题采用分治思想进行求解。与典型的分治问题不同,二分查找无需对子问题的结果进行合并,最小子问题的解即为原问题的解。 -1. **分解**:将数组的 $n$ 个元素分解为左右两个各包含 $\frac{n}{2}$ 个元素的子序列。 -2. **求解**:取中间元素 $nums[mid]$ 与 $target$ 相比。 - 1. 如果相等,则找到该元素; - 2. 如果 $nums[mid] < target,ドル则递归在左子序列中进行二分查找。 - 3. 如果 $nums[mid]> target,ドル则递归在右子序列中进行二分查找。 +具体步骤如下: -二分查找的的分治算法过程如下图所示。 +1. **分解**:将当前数组划分为左右两个子区间,每个子区间大致包含 $\frac{n}{2}$ 个元素。 +2. **处理**:选取中间元素 $nums[mid],ドル并与目标值 $target$ 进行比较: + 1. 如果 $nums[mid] == target,ドル则直接返回该元素下标; + 2. 如果 $nums[mid] < target,ドル则在右侧子区间递归查找; + 3. 如果 $nums[mid]> target,ドル则在左侧子区间递归查找。 + +下图展示了二分查找的分治过程。 ![二分查找的的分治算法过程](https://qcdn.itcharge.cn/images/20211223115032.png) @@ -246,6 +275,18 @@ class Solution: return left if nums[left] == target else -1 ``` +## 5. 总结 + +分治是一种「拆分—求解—合并」的通用思维范式:将大问题拆为若干规模更小且相互独立的同构子问题,递归(或迭代)求解到足够小的基例,最后自底向上合并结果。是否适合分治,取决于子问题是否独立、规模能否尽量均衡、以及合并是否足够高效。 + +实践中要关注三个要点: + +1. 明确且正确的递归基与边界,避免无穷递归与越界; +2. 尽量使子问题独立、规模均衡,必要时调整划分策略; +3. 评估合并代价,若合并过重或子问题高度重叠,应考虑动态规划、记忆化或改用其他范式。 + +合理运用这些原则,分治能在排序、查找、几何与数值计算等领域提供简洁而高效的解法。 + ## 练习题目 - [0050. Pow(x, n)](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0001-0099/powx-n.md) diff --git a/docs/07_algorithm/07_04_backtracking_algorithm.md b/docs/07_algorithm/07_04_backtracking_algorithm.md index 0950bf5e..4e490280 100644 --- a/docs/07_algorithm/07_04_backtracking_algorithm.md +++ b/docs/07_algorithm/07_04_backtracking_algorithm.md @@ -1,113 +1,133 @@ ## 1. 回溯算法简介 -> **回溯算法(Backtracking)**:一种能避免不必要搜索的穷举式的搜索算法。采用试错的思想,在搜索尝试过程中寻找问题的解,当探索到某一步时,发现原先的选择并不满足求解条件,或者还需要满足更多求解条件时,就退回一步(回溯)重新选择,这种走不通就退回再走的技术称为「回溯法」,而满足回溯条件的某个状态的点称为「回溯点」。 +> **回溯算法(Backtracking)**:回溯算法是一种系统地搜索所有可能解的算法,通过递归和试错的方式逐步构建解的过程。当发现当前路径无法满足题目要求或无法得到有效解时,算法会撤销上一步的选择(即「回溯」),返回到上一个决策点,尝试其他可能的路径。回溯法的核心思想是「走不通就退回,换条路再试」,而每次需要回退的节点称为「回溯点」。 -简单来说,回溯算法采用了一种 **「走不通就回退」** 的算法思想。 +简而言之,回溯算法就是「遇到死路就回头」。 -回溯算法通常用简单的递归方法来实现,在进行回溯过程中更可能会出现两种情况: +回溯算法常用递归方式实现,过程通常有两种结果: -1. 找到一个可能存在的正确答案; -2. 在尝试了所有可能的分布方法之后宣布该问题没有答案。 +1. 找到一个满足条件的解; +2. 尝试所有可能后,确认无解。 -## 2. 从全排列问题开始理解回溯算法 +## 2. 从全排列问题直观理解回溯算法 -以求解 $[1, 2, 3]$ 的全排列为例,我们来讲解一下回溯算法的过程。 +以 $[1, 2, 3]$ 的全排列为例,回溯算法的核心流程如下: -1. 选择以 1ドル$ 为开头的全排列。 - 1. 选择以 2ドル$ 为中间数字的全排列,则最后数字只能选择 3ドル$。即排列为:$[1, 2, 3]$。 - 2. 撤销选择以 3ドル$ 为最后数字的全排列,再撤销选择以 2ドル$ 为中间数字的全排列。然后选择以 3ドル$ 为中间数字的全排列,则最后数字只能选择 2ドル,ドル即排列为:$[1, 3, 2]$。 -2. 撤销选择以 2ドル$ 为最后数字的全排列,再撤销选择以 3ドル$ 为中间数字的全排列,再撤销选择以 1ドル$ 为开头的全排列。然后选择以 2ドル$ 开头的全排列。 - 1. 选择以 1ドル$ 为中间数字的全排列,则最后数字只能选择 3ドル$。即排列为:$[2, 1, 3]$。 - 2. 撤销选择以 3ドル$ 为最后数字的全排列,再撤销选择以 1ドル$ 为中间数字的全排列。然后选择以 3ドル$ 为中间数字的全排列,则最后数字只能选择 1ドル,ドル即排列为:$[2, 3, 1]$。 -3. 撤销选择以 1ドル$ 为最后数字的全排列,再撤销选择以 3ドル$ 为中间数字的全排列,再撤销选择以 2ドル$ 为开头的全排列,选择以 3ドル$ 开头的全排列。 - 1. 选择以 1ドル$ 为中间数字的全排列,则最后数字只能选择 2ドル$。即排列为:$[3, 1, 2]$。 - 2. 撤销选择以 2ドル$ 为最后数字的全排列,再撤销选择以 1ドル$ 为中间数字的全排列。然后选择以 2ドル$ 为中间数字的全排列,则最后数字只能选择 1ドル,ドル即排列为:$[3, 2, 1]$。 +1. 首先选择第一个数字为 1ドル$: + - 接下来可选数字为 2ドル$ 和 3ドル$。 + - 选择 2ドル$ 作为第二个数字,剩下只能选 3ドル,ドル得到排列 $[1, 2, 3]$。 + - 回退一步,撤销 3ドル,ドル撤销 2ドル,ドル尝试 3ドル$ 作为第二个数字,剩下只能选 2ドル,ドル得到排列 $[1, 3, 2]$。 -总结一下全排列的回溯过程: +2. 回退到最初,撤销 1ドル,ドル尝试以 2ドル$ 开头: + - 接下来可选数字为 1ドル$ 和 3ドル$。 + - 选择 1ドル$ 作为第二个数字,剩下只能选 3ドル,ドル得到排列 $[2, 1, 3]$。 + - 回退一步,撤销 3ドル,ドル撤销 1ドル,ドル尝试 3ドル$ 作为第二个数字,剩下只能选 1ドル,ドル得到排列 $[2, 3, 1]$。 -- **按顺序枚举每一位上可能出现的数字,之前已经出现的数字在接下来要选择的数字中不能再次出现。** -- 对于每一位,进行如下几步: - 1. **选择元素**:从可选元素列表中选择一个之前没有出现过的元素。 - 2. **递归搜索**:从选择的元素出发,一层层地递归搜索剩下位数,直到遇到边界条件时,不再向下搜索。 - 3. **撤销选择**:一层层地撤销之前选择的元素,转而进行另一个分支的搜索。直到完全遍历完所有可能的路径。 +3. 再回退到最初,撤销 2ドル,ドル尝试以 3ドル$ 开头: + - 接下来可选数字为 1ドル$ 和 2ドル$。 + - 选择 1ドル$ 作为第二个数字,剩下只能选 2ドル,ドル得到排列 $[3, 1, 2]$。 + - 回退一步,撤销 2ドル,ドル撤销 1ドル,ドル尝试 2ドル$ 作为第二个数字,剩下只能选 1ドル,ドル得到排列 $[3, 2, 1]$。 -对于上述决策过程,我们也可以用一棵决策树来表示: +简而言之,每次选择一个数字作为当前位置的元素,递归地选择下一个位置的数字。当所有数字都被选完时,得到一个完整的排列;如果发现当前选择无法继续,则回退到上一步,尝试其他可能性。这样就能系统地枚举出所有全排列。 + +全排列的回溯过程可以简要归纳为: + +- **逐位枚举每个位置可能出现的数字,且每个数字在同一排列中只出现一次。** +- 对于每一位,遵循以下步骤: + 1. **选择元素**:从当前可选的数字中,挑选一个未被使用的数字。 + 2. **递归探索**:将该数字加入当前路径,递归进入下一层,继续选择下一个位置的数字,直到满足终止条件(如路径长度等于数组长度)。 + 3. **撤销选择(回溯)**:递归返回后,移除刚才选择的数字,恢复现场,尝试其他未选过的数字,探索不同的分支,直到所有可能路径都被遍历。 + +上述决策过程可以用一棵决策树形象表示: ![全排列问题的决策树](https://qcdn.itcharge.cn/images/20220425102048.png) -从全排列的决策树中我们可以看出: +从全排列的决策树结构可以看出: -- 每一层中有一个或多个不同的节点,这些节点以及节点所连接的分支代表了「不同的选择」。 -- 每一个节点代表了求解全排列问题的一个「状态」,这些状态是通过「不同的值」来表现的。 -- 每向下递推一层就是在「可选元素列表」中选择一个「元素」加入到「当前状态」。 -- 当一个决策分支探索完成之后,会逐层向上进行回溯。 -- 每向上回溯一层,就是把所选择的「元素」从「当前状态」中移除,回退到没有选择该元素时的状态(或者说重置状态),从而进行其他分支的探索。 +- 每一层代表当前递归的深度,每个节点及其分支对应一次不同的选择。 +- 每个节点表示当前排列的一个「状态」,即已选择的数字序列。 +- 向下递归一层,相当于在可选数字中再选一个数字加入当前状态。 +- 当某条分支探索结束后,递归会逐层回退(回溯),撤销最近的选择,恢复到上一个状态,继续尝试其他分支。 -根据上文的思路和决策树,我们来写一下全排列的回溯算法代码(假设给定数组 $nums$ 中不存在重复元素)。则代码如下所示: +基于上述思路和决策树结构,下面给出全排列问题的回溯算法代码(假设输入数组 $nums$ 无重复元素): ```python class Solution: def permute(self, nums: List[int]) -> List[List[int]]: - res = [] # 存放所有符合条件结果的集合 - path = [] # 存放当前符合条件的结果 - def backtracking(nums): # nums 为选择元素列表 - if len(path) == len(nums): # 说明找到了一组符合条件的结果 - res.append(path[:]) # 将当前符合条件的结果放入集合中 + """ + 回溯法求解全排列问题 + :param nums: 输入的数字列表 + :return: 所有可能的全排列 + """ + res = [] # 用于存放所有符合条件的排列结果 + path = [] # 用于存放当前递归路径下的排列 + + def backtracking(): + # 递归终止条件:当 path 长度等于 nums 长度时,说明找到一个完整排列 + if len(path) == len(nums): + res.append(path[:]) # 注意要拷贝一份 path,否则后续 path 变化会影响结果 return - for i in range(len(nums)): # 枚举可选元素列表 - if nums[i] not in path: # 从当前路径中没有出现的数字中选择 - path.append(nums[i]) # 选择元素 - backtracking(nums) # 递归搜索 - path.pop() # 撤销选择 - - backtracking(nums) + # 遍历所有可选的数字 + for i in range(len(nums)): + if nums[i] in path: + # 如果当前数字已经在 path 中,跳过,保证每个数字只出现一次 + continue + # 做选择:将当前数字加入 path + path.append(nums[i]) + # 递归进入下一层,继续选择下一个数字 + backtracking() + # 撤销选择:回退到上一步,移除最后一个数字,尝试其他分支 + path.pop() + + backtracking() return res ``` -## 3. 回溯算法的通用模板 +## 3. 回溯算法通用模板 -根据上文全排列的回溯算法代码,我们可以提炼出回溯算法的通用模板,回溯算法的通用模板代码如下所示: +结合前文全排列问题的回溯实现,我们可以总结出一套简洁高效的回溯算法通用模板,具体如下: ```python -res = [] # 存放所欲符合条件结果的集合 -path = [] # 存放当前符合条件的结果 -def backtracking(nums): # nums 为选择元素列表 - if 遇到边界条件: # 说明找到了一组符合条件的结果 - res.append(path[:]) # 将当前符合条件的结果放入集合中 +res = [] # 存放所有符合条件结果的集合 +path = [] # 存放当前递归路径下的结果 + +def backtracking(nums): + """ + 回溯算法通用模板 + :param nums: 可选元素列表 + """ + # 递归终止条件:根据具体问题设定(如 path 满足特定条件) + if 满足结束条件: # 例如:len(path) == len(nums) + res.append(path[:]) # 注意要拷贝一份 path,避免后续修改影响结果 return - for i in range(len(nums)): # 枚举可选元素列表 - path.append(nums[i]) # 选择元素 - backtracking(nums) # 递归搜索 - path.pop() # 撤销选择 + # 遍历所有可选的元素 + for i in range(len(nums)): + # 可选:根据具体问题添加剪枝条件,如元素不能重复选取 + # if nums[i] in path: + # continue + + path.append(nums[i]) # 做选择,将当前元素加入 path + backtracking(nums) # 递归,继续选择下一个元素 + path.pop() # 撤销选择,回退到上一步状态 +# 调用回溯函数,开始搜索 backtracking(nums) ``` -## 4. 回溯算法三步走 - -网络上给定的回溯算法解题步骤比较抽象,这里只做一下简单介绍。 +## 4. 回溯算法的基本步骤 -1. **根据所给问题,定义问题的解空间**:要定义合适的解空间,包括解的组织形式和显约束。 - - **解的组织形式**:将解的组织形式都规范为一个 $n$ 元组 ${x_1, x_2 ..., x_n}$。 - - **显约束**:对解分量的取值范围的限定,可以控制解空间的大小。 -2. **确定解空间的组织结构**:解空间的组织结构通常以解空间树的方式形象地表达,根据解空间树的不同,解空间分为子集树、排列树、$m$ 叉树等。 -3. **搜索解空间**:按照深度优先搜索策略,根据隐约束(约束函数和限界函数),在解空间中搜索问题的可行解或最优解。当发现当 前节点不满足求解条件时,就回溯,尝试其他路径。 - - 如果问题只是求可行解,则只需设定约束函数即可,如果要求最优解,则需要设定约束函数和限界函数。 +回溯算法的核心思想是:**通过深度优先搜索,不断尝试所有可能的选择,当发现当前路径不满足条件时就回退(回溯),尝试其他路径,最终找到所有可行解或最优解。** -这种回溯算法的解题步骤太过于抽象,不利于我们在日常做题时进行思考。其实在递归算法知识的相关章节中,我们根据递归的基本思想总结了递归三步走的书写步骤。同样,根据回溯算法的基本思想,我们也来总结一下回溯算法三步走的书写步骤。 +回溯算法的基本步骤如下: -回溯算法的基本思想是:**以深度优先搜索的方式,根据产生子节点的条件约束,搜索问题的解。当发现当前节点已不满足求解条件时,就「回溯」返回,尝试其他的路径。** - -那么,在写回溯算法时,我们可以按照这个思想来书写回溯算法,具体步骤如下: - -1. **明确所有选择**:画出搜索过程的决策树,根据决策树来确定搜索路径。 -2. **明确终止条件**:推敲出递归的终止条件,以及递归终止时的要执行的处理方法。 -3. **将决策树和终止条件翻译成代码**: - 1. 定义回溯函数(明确函数意义、传入参数、返回结果等)。 - 2. 书写回溯函数主体(给出约束条件、选择元素、递归搜索、撤销选择部分)。 - 3. 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 +1. **明确所有选择**:画出决策树,理清每一步有哪些可选项。每个节点的分支代表一次选择。 +2. **明确终止条件**:终止条件通常是递归到某一深度、遍历完所有元素或满足题目要求。到达终止条件时,处理当前结果(如加入答案集)。 +3. **将决策树和终止条件转化为代码**: + - 定义回溯函数(明确函数意义、传入参数、返回结果等)。 + - 书写回溯函数主体(给出约束条件、选择元素、递归搜索、撤销选择部分)。 + - 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 ### 4.1 明确所有选择 @@ -115,51 +135,61 @@ backtracking(nums) ### 4.2 明确终止条件 -回溯算法的终止条件也就是决策树的底层,即达到无法再做选择的条件。 - -回溯函数的终止条件一般为给定深度、叶子节点、非叶子节点(包括根节点)、所有节点等。并且还要给出在终止条件下的处理方法,比如输出答案,将当前符合条件的结果放入集合中等等。 +回溯算法的终止条件,通常对应于决策树的叶子节点,即到达无法继续做选择的位置。 -### 4.3 将决策树和终止条件翻译成代码 +常见的终止条件包括:递归达到指定深度、遍历到叶子节点、遍历完所有元素等。此时需要对当前路径进行处理,例如将符合要求的结果加入答案集合,或输出当前解等。 -在明确所有选择和明确终止条件之后,我们就可以将其翻译成代码了。这一步也可以分为 3ドル$ 步来做: - -1. 定义回溯函数(明确函数意义、传入参数、返回结果等)。 -2. 书写回溯函数主体(给出约束条件、选择元素、递归搜索、撤销选择部分)。 -3. 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 +### 4.3 将决策树和终止条件转化为代码 #### 4.3.1 定义回溯函数 -在定义回溯函数时,一定要明确递归函数的意义,也就是要明白这个问题的传入参数和全局变量是什么,最终返回的结果是要解决的什么问题。 - -- **传入参数和全局变量**:是由递归搜索阶段时的「当前状态」来决定的。最好是能通过传入参数和全局变量直接记录「当前状态」。 +在定义回溯函数时,首先要清晰地界定递归函数的含义:即该函数的参数、全局变量分别代表什么,以及最终希望通过递归解决什么问题。 -比如全排列中,`backtracking(nums)` 这个函数的传入参数是 $nums$(可选择的元素列表),全局变量是 $res$(存放所有符合条件结果的集合数组)和 $path$(存放当前符合条件的结果)。$nums$ 表示当前可选的元素,$path$ 用于记录递归搜索阶段的「当前状态」。$res$ 则用来保存递归搜索阶段的「所有状态」。 +- **参数与全局变量设计**:参数和全局变量应能完整表达递归过程中的「当前状态」。通常,参数用于传递当前可选的元素、已做出的选择等信息,全局变量则用于收集所有满足条件的解。 -- **返回结果**:返回结果是在遇到递归终止条件时,需要向上一层函数返回的信息。 +以全排列问题为例,`backtracking(nums)` 的参数 $nums$ 表示当前可选的元素列表,全局变量 $path$ 记录当前递归路径(已选择的元素),$res$ 用于存储所有符合条件的结果。这样,$nums$ 反映可选空间,$path$ 反映当前状态,$res$ 汇总所有解。 -一般回溯函数的返回结果都是单个节点或单个数值,告诉上一层函数我们当前的搜索结果是什么即可。 +- **返回值设计**:回溯函数的返回值通常用于在递归终止时向上一层传递结果。大多数情况下,回溯函数只需返回单个节点或数值,表明当前搜索的结果。 -当然,如果使用全局变量来保存「当前状态」的话,也可以不需要向上一层函数返回结果,即返回空结果。比如上文中的全排列。 +如果采用全局变量(如 $res$)来收集所有解,则回溯函数可以不显式返回结果,直接 return 即可。例如全排列问题中,递归终止时将 $path$ 加入 $res,ドル无需返回值。 #### 4.3.2 书写回溯函数主体 -根据当前可选择的元素列表、给定的约束条件(例如之前已经出现的数字在接下来要选择的数字中不能再次出现)、存放当前状态的变量,我们就可以写出回溯函数的主体部分了。即: +结合当前可选元素、题目约束(如某元素不可重复选择)、以及用于记录当前路径的变量,我们即可编写回溯函数的核心主体部分。即: ```python -for i in range(len(nums)): # 枚举可选元素列表 - if 满足约束条件: # 约束条件 - path.append(nums[i]) # 选择元素 - backtracking(nums) # 递归搜索 - path.pop() # 撤销选择 +for 选择 in 可选列表: + if 满足约束: + 做选择 + backtrack(新参数) + 撤销选择 ``` #### 4.3.3 明确递归终止条件 -这一步其实就是将「4.2 明确终止条件」章节中的递归终止条件和终止条件下的处理方法转换为代码中的条件语句和对应的执行语句。 +这一环节的本质,是将「4.2 明确终止条件」中分析得到的递归终止条件及其对应的处理逻辑,具体实现为代码中的判断语句和相应的操作。例如,判断是否达到递归深度或满足题目要求,并在满足时将当前结果加入答案集等。 + +#### 4.3.4 回溯函数通用模板 + +通过上述三步分析,我们可以归纳出回溯算法的核心流程:**首先枚举所有可选项,然后判断是否满足终止条件,最后递归深入,并在必要时撤销选择进行回溯**。这种结构化的思考方式,使回溯算法能够高效地解决组合、排列、子集等典型问题。接下来,我们将结合具体例题,进一步体会回溯算法在实际问题中的应用与实现。 + +回溯通用模板如下: + +```python +def backtrack(参数): + if 终止条件: + 处理结果 + return + for 选择 in 可选列表: + if 满足约束: + 做选择 + backtrack(新参数) + 撤销选择 +``` ## 5. 回溯算法的应用 -### 5.1 子集 +### 5.1 经典例题:子集 #### 5.1.1 题目链接 @@ -197,62 +227,77 @@ for i in range(len(nums)): # 枚举可选元素列表 ##### 思路 1:回溯算法 -数组的每个元素都有两个选择:选与不选。 +对于数组中的每个元素,都有「选择」或「不选择」两种可能。 -我们可以通过向当前子集数组中添加可选元素来表示选择该元素。也可以在当前递归结束之后,将之前添加的元素从当前子集数组中移除(也就是回溯)来表示不选择该元素。 +我们可以通过将元素加入当前子集(path)来表示「选择」,递归结束后再将其移除(即回溯),从而实现「撤销选择」,表示「不选择」该元素。 -下面我们根据回溯算法三步走,写出对应的回溯算法。 +下面结合回溯算法的三大步骤,梳理子集问题的解题思路: ![子集的决策树](https://qcdn.itcharge.cn/images/20220425210640.png) -1. **明确所有选择**:根据数组中每个位置上的元素选与不选两种选择,画出决策树,如上图所示。 +1. **明确所有选择**:对于数组的每个位置,都可以选择是否将该元素加入当前子集。决策树的每一层对应一个元素的选择与否。 2. **明确终止条件**: - - 当遍历到决策树的叶子节点时,就终止了。即当前路径搜索到末尾时,递归终止。 -3. **将决策树和终止条件翻译成代码**: + - 当递归遍历到数组末尾(即所有元素都被考虑过)时,递归终止。 +3. **将思路转化为代码实现**: 1. 定义回溯函数: - - `backtracking(nums, index):` 函数的传入参数是 $nums$(可选数组列表)和 $index$(代表当前正在考虑元素是 $nums[i]$),全局变量是 $res$(存放所有符合条件结果的集合数组)和 $path$(存放当前符合条件的结果)。 - - `backtracking(nums, index):` 函数代表的含义是:在选择 $nums[index]$ 的情况下,递归选择剩下的元素。 - 2. 书写回溯函数主体(给出选择元素、递归搜索、撤销选择部分)。 - - 从当前正在考虑元素,到数组结束为止,枚举出所有可选的元素。对于每一个可选元素: - - 约束条件:之前选过的元素不再重复选用。每次从 $index$ 位置开始遍历而不是从 0ドル$ 位置开始遍历就是为了避免重复。集合跟全排列不一样,子集中 ${1, 2}$ 和 ${2, 1}$ 是等价的。为了避免重复,我们之前考虑过的元素,就不再重复考虑了。 - - 选择元素:将其添加到当前子集数组 $path$ 中。 - - 递归搜索:在选择该元素的情况下,继续递归考虑下一个位置上的元素。 - - 撤销选择:将该元素从当前子集数组 $path$ 中移除。 + - `backtracking(nums, index)`,其中 $nums$ 是原始数组,$index$ 表示当前递归到的元素下标。全局变量 $res$ 用于存储所有子集结果,$path$ 用于存储当前子集路径。 + - 该函数的含义是:从 $index$ 开始,依次尝试将后续元素加入子集,递归搜索所有可能的组合。 + 2. 编写回溯主体逻辑(选择、递归、回溯): + - 从 $index$ 开始,依次枚举每个可选元素。对于每个元素: + - **去重约束**:每次递归都从 $index$ 开始,避免重复选择已考虑过的元素,保证子集不重复(如 {1,2} 和 {2,1} 视为同一子集)。 + - **选择**:将当前元素加入 $path$。 + - **递归**:递归进入下一层,继续选择下一个元素。 + - **回溯**:递归返回后,移除刚刚加入的元素,恢复现场,尝试其他分支。 ```python - for i in range(index, len(nums)): # 枚举可选元素列表 - path.append(nums[i]) # 选择元素 - backtracking(nums, i + 1) # 递归搜索 - path.pop() # 撤销选择 + # 从当前下标开始,依次尝试选择每个元素 + for i in range(index, len(nums)): + path.append(nums[i]) # 选择当前元素,加入子集 + backtracking(i + 1) # 递归,继续选择下一个元素 + path.pop() # 撤销选择,回溯到上一步 ``` - 3. 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 - - 当遍历到决策树的叶子节点时,就终止了。也就是当正在考虑的元素位置到达数组末尾(即 $start \ge len(nums)$)时,递归停止。 - - 从决策树中也可以看出,子集需要存储的答案集合应该包含决策树上所有的节点,应该需要保存递归搜索的所有状态。所以无论是否达到终止条件,我们都应该将当前符合条件的结果放入到集合中。 + 3. 明确递归终止条件及结果处理: + - 每次进入回溯函数时,都将当前 $path$ 加入结果集 $res,ドル因为子集问题需要收集所有状态(包括中间状态和叶子节点)。 + - 当 $index \ge len(nums)$ 时,递归自然终止,无需额外处理。 + +简而言之,回溯法通过「选择 - 递归 - 回溯」三步,系统地枚举所有子集,并通过合理的约束避免重复。 ##### 思路 1:代码 ```python class Solution: def subsets(self, nums: List[int]) -> List[List[int]]: - res = [] # 存放所有符合条件结果的集合 - path = [] # 存放当前符合条件的结果 - def backtracking(nums, index): # 正在考虑可选元素列表中第 index 个元素 - res.append(path[:]) # 将当前符合条件的结果放入集合中 - if index>= len(nums): # 遇到终止条件(本题) + """ + 回溯法求解子集问题。 + :param nums: 输入数组 + :return: 所有子集的列表 + """ + res = [] # 用于存放所有子集结果 + path = [] # 用于存放当前递归路径上的子集 + + def backtracking(index: int): + """ + 回溯函数,递归枚举所有子集。 + :param index: 当前递归到的元素下标 + """ + # 每次进入回溯函数,都将当前路径(子集)加入结果集 + res.append(path[:]) + # 递归终止条件:index 超过数组长度时返回 + if index>= len(nums): return + # 从当前下标开始,依次尝试选择每个元素 + for i in range(index, len(nums)): + path.append(nums[i]) # 选择当前元素,加入子集 + backtracking(i + 1) # 递归,继续选择下一个元素 + path.pop() # 撤销选择,回溯到上一步 - for i in range(index, len(nums)): # 枚举可选元素列表 - path.append(nums[i]) # 选择元素 - backtracking(nums, i + 1) # 递归搜索 - path.pop() # 撤销选择 - - backtracking(nums, 0) + backtracking(0) # 从下标 0 开始递归 return res ``` ##### 思路 1:复杂度分析 -- **时间复杂度**:$O(n \times 2^n),ドル其中 $n$ 指的是数组 $nums$ 的元素个数,2ドル^n$ 指的是所有状态数。每种状态需要 $O(n)$ 的时间来构造子集。 -- **空间复杂度**:$O(n),ドル每种状态下构造子集需要使用 $O(n)$ 的空间。 +- **时间复杂度**:$O(n \times 2^n)$。其中 $n$ 是数组 $nums$ 的元素个数。回溯过程中,每个元素有选与不选两种状态,共 2ドル^n$ 种子集,每生成一个子集需要 $O(n)$ 的时间(因为要拷贝 path 到结果集)。 +- **空间复杂度**:$O(n)$。递归过程中 path 最深为 $n,ドル递归栈空间也是 $O(n)$。 ### 5.2 N 皇后 @@ -288,94 +333,91 @@ class Solution: ##### 思路 1:回溯算法 -这道题是经典的回溯问题。我们可以按照行序来放置皇后,也就是先放第一行,再放第二行 ...... 一直放到最后一行。 - -对于 $n \times n$ 的棋盘来说,每一行有 $n$ 列,也就有 $n$ 种放法可供选择。我们可以尝试选择其中一列,查看是否与之前放置的皇后有冲突,如果没有冲突,则继续在下一行放置皇后。依次类推,直到放置完所有皇后,并且都不发生冲突时,就得到了一个合理的解。 +本题是回溯算法的经典应用。我们按照「逐行放置皇后」的顺序进行搜索:即先在第 1 行放皇后,再到第 2 行,依次递归,直到最后一行。 -并且在放置完之后,通过回溯的方式尝试其他可能的分支。 +对于 $n \times n$ 的棋盘,每一行有 $n$ 个位置可选。每次尝试将皇后放在当前行的某一列,并判断该位置是否与之前已放置的皇后冲突(即是否在同一列、主对角线、副对角线上)。如果不冲突,则递归进入下一行继续放置;若冲突,则跳过该位置,尝试下一列。所有皇后都成功放置后,即得到一个有效解。回溯算法会自动探索所有可能的分支,确保所有解都被枚举。 -下面我们根据回溯算法三步走,写出对应的回溯算法。 +下面结合回溯算法的"三步走"思想,梳理 N 皇后问题的解题流程: ![](https://qcdn.itcharge.cn/images/20220426095225.png) -1. **明确所有选择**:根据棋盘中当前行的所有列位置上是否选择放置皇后,画出决策树,如上图所示。 +1. **明确所有选择**:对于当前行,依次尝试将皇后放在每一列的不同位置,每个位置都代表一次选择,整个过程可用决策树表示(如上图)。 2. **明确终止条件**: - - 当遍历到决策树的叶子节点时,就终止了。也就是在最后一行放置完皇后时,递归终止。 -3. **将决策树和终止条件翻译成代码:** + - 当所有行都已成功放置皇后(即递归到第 $n$ 行),说明找到一个有效解,此时递归终止。 +3. **将决策树和终止条件转化为代码实现:** 1. 定义回溯函数: - - 首先我们先使用一个 $n \times n$ 大小的二维矩阵 $chessboard$ 来表示当前棋盘,$chessboard$ 中的字符 `Q` 代表皇后,`.` 代表空位,初始都为 `.`。 - - 然后定义回溯函数 `backtrack(chessboard, row): ` 函数的传入参数是 $chessboard$(棋盘数组)和 $row$(代表当前正在考虑放置第 $row$ 行皇后),全局变量是 $res$(存放所有符合条件结果的集合数组)。 - - `backtrack(chessboard, row):` 函数代表的含义是:在放置好第 $row$ 行皇后的情况下,递归放置剩下行的皇后。 - 2. 书写回溯函数主体(给出选择元素、递归搜索、撤销选择部分)。 - - 枚举出当前行所有的列。对于每一列位置: - - 约束条件:定义一个判断方法,先判断一下当前位置是否与之前棋盘上放置的皇后发生冲突,如果不发生冲突则继续放置,否则则继续向后遍历判断。 - - 选择元素:选择 $row, col$ 位置放置皇后,将其棋盘对应位置设置为 `Q`。 - - 递归搜索:在该位置放置皇后的情况下,继续递归考虑下一行。 - - 撤销选择:将棋盘上 $row, col$ 位置设置为 `.`。 - ```python - # 判断当前位置 row, col 是否与之前放置的皇后发生冲突 - def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]): - for i in range(row): - if chessboard[i][col] == 'Q': - return False - - i, j = row - 1, col - 1 - while i>= 0 and j>= 0: - if chessboard[i][j] == 'Q': - return False - i -= 1 - j -= 1 - i, j = row - 1, col + 1 - while i>= 0 and j < n: - if chessboard[i][j] == 'Q': - return False - i -= 1 - j += 1 - - return True - ``` - + - 使用一个 $n \times n$ 的二维数组 $chessboard$ 表示棋盘,`Q` 表示皇后,`.` 表示空位,初始均为 `.`。 + - 定义回溯函数 `backtrack(chessboard, row)`,其中 $chessboard$ 为当前棋盘状态,$row$ 表示当前正在处理的行,全局变量 $res$ 用于收集所有可行解。 + - `backtrack(chessboard, row)` 的含义是:在前 $row-1$ 行已放置皇后的前提下,递归尝试为第 $row$ 行放置皇后。 + 2. 编写回溯函数主体(包括选择、递归、撤销选择): + - 遍历当前行的每一列,对于每个位置: + - 约束条件:通过辅助函数判断当前位置是否与已放置的皇后冲突,若无冲突则继续,否则跳过。 + - 选择:在 $row, col$ 位置放置皇后(即 $chessboard[row][col] = 'Q'$)。 + - 递归:递归处理下一行($row+1$)。 + - 撤销选择:回溯时将 $chessboard[row][col]$ 恢复为 `.`,以便尝试其他方案。 ```python - for col in range(n): # 枚举可放置皇后的列 - if self.isValid(n, row, col, chessboard): # 如果该位置与之前放置的皇后不发生冲突 - chessboard[row][col] = 'Q' # 选择 row, col 位置放置皇后 - backtrack(row + 1, chessboard) # 递归放置 row + 1 行之后的皇后 - chessboard[row][col] = '.' # 撤销选择 row, col 位置 + # 枚举当前行的每一列,尝试放置皇后 + for col in range(n): + if self.isValid(n, row, col, chessboard): # 检查当前位置是否合法 + chessboard[row][col] = 'Q' # 放置皇后 + self.backtrack(n, row + 1, chessboard) # 递归处理下一行 + chessboard[row][col] = '.' # 撤销选择,回溯 ``` - 3. 明确递归终止条件(给出递归终止条件,以及递归终止时的处理方法)。 - - 当遍历到决策树的叶子节点时,就终止了。也就是在最后一行放置完皇后(即 $row == n$)时,递归停止。 - - 递归停止时,将当前符合条件的棋盘转换为答案需要的形式,然后将其存入答案数组 $res$ 中即可。 + 3. 明确递归终止条件(即何时递归应当结束,以及结束时如何处理结果)。 + - 当递归到第 $n$ 行(即 $row == n$)时,说明所有皇后已成功放置,此时到达决策树的叶子节点,递归终止。 + - 终止时,将当前棋盘状态转换为题目要求的格式,并加入结果集 $res$。 ##### 思路 1:代码 ```python class Solution: - res = [] + res = [] # 用于存储所有可行解 + def backtrack(self, n: int, row: int, chessboard: List[List[str]]): + """ + 回溯主函数:在第 row 行尝试放置皇后 + :param n: 棋盘大小(n x n) + :param row: 当前递归到的行号 + :param chessboard: 当前棋盘状态 + """ if row == n: + # 递归终止条件:所有行都已放置皇后,记录当前棋盘方案 temp_res = [] for temp in chessboard: - temp_str = ''.join(temp) + temp_str = ''.join(temp) # 将每一行转为字符串 temp_res.append(temp_str) self.res.append(temp_res) return + # 枚举当前行的每一列,尝试放置皇后 for col in range(n): - if self.isValid(n, row, col, chessboard): - chessboard[row][col] = 'Q' - self.backtrack(n, row + 1, chessboard) - chessboard[row][col] = '.' + if self.isValid(n, row, col, chessboard): # 检查当前位置是否合法 + chessboard[row][col] = 'Q' # 放置皇后 + self.backtrack(n, row + 1, chessboard) # 递归处理下一行 + chessboard[row][col] = '.' # 撤销选择,回溯 def isValid(self, n: int, row: int, col: int, chessboard: List[List[str]]): + """ + 检查在 (row, col) 位置放置皇后是否合法 + :param n: 棋盘大小 + :param row: 当前行 + :param col: 当前列 + :param chessboard: 当前棋盘状态 + :return: True 表示合法,False 表示冲突 + """ + # 检查同一列是否有皇后 for i in range(row): if chessboard[i][col] == 'Q': return False + # 检查左上对角线是否有皇后 i, j = row - 1, col - 1 while i>= 0 and j>= 0: if chessboard[i][j] == 'Q': return False i -= 1 j -= 1 + + # 检查右上对角线是否有皇后 i, j = row - 1, col + 1 while i>= 0 and j < n: if chessboard[i][j] == 'Q': @@ -383,12 +425,18 @@ class Solution: i -= 1 j += 1 - return True + return True # 没有冲突,可以放置 def solveNQueens(self, n: int) -> List[List[str]]: - self.res.clear() + """ + 主入口函数,返回所有 N 皇后问题的解 + :param n: 棋盘大小 + :return: 所有可行解的列表 + """ + self.res.clear() # 清空历史结果 + # 初始化棋盘,全部填充为 '.' chessboard = [['.' for _ in range(n)] for _ in range(n)] - self.backtrack(n, 0, chessboard) + self.backtrack(n, 0, chessboard) # 从第 0 行开始回溯 return self.res ``` @@ -397,6 +445,16 @@ class Solution: - **时间复杂度**:$O(n!),ドル其中 $n$ 是皇后数量。 - **空间复杂度**:$O(n^2),ドル其中 $n$ 是皇后数量。递归调用层数不会超过 $n,ドル每个棋盘的空间复杂度为 $O(n^2),ドル所以空间复杂度为 $O(n^2)$。 +## 6. 总结 + +回溯算法是一种通过递归和试错来系统地搜索所有可能解的算法。其核心思想是「走不通就退回,换条路再试」,通过深度优先搜索的方式遍历决策树,当发现当前路径无法满足条件时,会撤销上一步的选择并尝试其他可能性。 + +回溯算法的关键在于「选择 - 递归 - 回溯」:首先做出选择,然后递归进入下一层继续搜索,最后在递归返回时撤销选择,恢复到之前的状态。这种机制使得算法能够穷尽所有可能的解空间,特别适用于需要枚举所有可能解的问题。 + +回溯算法在解决组合、排列、子集等经典问题中表现出色,如全排列、N皇后、子集生成等。其通用模板简洁明了,通过明确所有选择、确定终止条件、转化为代码实现三个步骤,可以高效地解决各种回溯类问题。 + +虽然回溯算法能够保证找到所有解,但其时间复杂度通常较高,特别是在解空间较大时。因此,在实际应用中需要结合剪枝等优化技巧来提高效率,避免不必要的搜索路径。 + ## 练习题目 - [0046. 全排列](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0001-0099/permutations.md) diff --git a/docs/07_algorithm/07_05_greedy_algorithm.md b/docs/07_algorithm/07_05_greedy_algorithm.md index 0691a88c..7ccc9521 100644 --- a/docs/07_algorithm/07_05_greedy_algorithm.md +++ b/docs/07_algorithm/07_05_greedy_algorithm.md @@ -2,77 +2,68 @@ ### 1.1 贪心算法的定义 -> **贪心算法(Greedy Algorithm)**:一种在每次决策时,总是采取在当前状态下的最好选择,从而希望导致结果是最好或最优的算法。 +> **贪心算法(Greedy Algorithm)**:每一步都选择当前最优(看起来最好的)方案,期望通过一系列局部最优,最终获得全局最优解。 -贪心算法是一种改进的「分步解决算法」,其核心思想是:将求解过程分成「若干个步骤」,然后根据题意选择一种「度量标准」,每个步骤都应用「贪心原则」,选取当前状态下「最好 / 最优选择(局部最优解)」,并以此希望最后得出的结果也是「最好 / 最优结果(全局最优解)」。 +贪心算法的核心思想是:将问题分解为若干步骤,每一步都根据当前情况,按照某种标准选择最优解(即「贪心」选择),不回头、不考虑整体,只关注当前最优。这样可以避免穷举所有可能,大大简化求解过程。 -换句话说,贪心算法不从整体最优上加以考虑,而是一步一步进行,每一步只以当前情况为基础,根据某个优化测度做出局部最优选择,从而省去了为找到最优解要穷举所有可能所必须耗费的大量时间。 +简而言之,贪心算法每次只做出当前看来最优的选择,期望通过一系列这样的选择得到整体最优解。 ### 1.2 贪心算法的特征 -对许多问题来说,可以使用贪心算法,通过局部最优解而得到整体最优解或者是整体最优解的近似解。但并不是所有问题,都可以使用贪心算法的。 +贪心算法适用于一类特殊问题:只要每一步都做出当前最优选择,最终就能得到整体最优解或近似最优解。但并非所有问题都适用贪心算法。 -一般来说,这些能够使用贪心算法解决的问题必须满足下面的两个特征: +通常,能用贪心算法解决的问题需同时满足两个条件: -1. **贪心选择性质** +1. **贪心选择性质** 2. **最优子结构** #### 1.2.1 贪心选择性质 -> **贪心选择性质**:指的是一个问题的全局最优解可以通过一系列局部最优解(贪心选择)来得到。 +> **贪心选择性质**:全局最优解可以通过一系列局部最优(贪心)选择获得。 -换句话说,当进行选择时,我们直接做出在当前问题中看来最优的选择,而不用去考虑子问题的解。在做出选择之后,才会去求解剩下的子问题,如下图所示。 +也就是说,每次只需关注当前最优选择,无需关心子问题的解。做出选择后,再递归处理剩下的子问题。 ![贪心选择性质](https://qcdn.itcharge.cn/images/20240513163300.png) -贪心算法在进行选择时,可能会依赖之前做出的选择,但不会依赖任何将来的选择或是子问题的解。运用贪心算法解决的问题在程序的运行过程中无回溯过程。 +贪心算法的每一步可能依赖之前的选择,但不会回溯,也不依赖未来的选择或子问题的解。 #### 1.2.2 最优子结构性质 -> **最优子结构性质**:指的是一个问题的最优解包含其子问题的最优解。 +> **最优子结构性质**:问题的最优解包含其子问题的最优解。 -问题的最优子结构性质是该问题能否用贪心算法求解的关键。 - -举个例子,如下图所示,原问题 $S = \lbrace a_1, a_2, a_3, a_4 \rbrace,ドル在 $a_1$ 步我们通过贪心选择选出一个当前最优解之后,问题就转换为求解子问题 $S_{\text{子问题}} = \lbrace a_2, a_3, a_4 \rbrace$。如果原问题 $S$ 的最优解可以由「第 $a_1$ 步通过贪心选择的局部最优解」和「 $S_{\text{子问题}}$ 的最优解」构成,则说明该问题满足最优子结构性质。 - -也就是说,如果原问题的最优解包含子问题的最优解,则说明该问题满足最优子结构性质。 +这是贪心算法成立的关键。举例来说,假设原问题 $S = \lbrace a_1, a_2, a_3, a_4 \rbrace,ドル第一步通过贪心选择得到当前最优解,剩下的子问题 $S_{\text{子问题}} = \lbrace a_2, a_3, a_4 \rbrace$。如果原问题的最优解等于「当前贪心选择」加上「子问题的最优解」,则满足最优子结构。 ![最优子结构性质](https://qcdn.itcharge.cn/images/20240513163310.png) -在做了贪心选择后,满足最优子结构性质的原问题可以分解成规模更小的类似子问题来解决,并且可以通过贪心选择和子问题的最优解推导出问题的最优解。 - -反之,如果不能利用子问题的最优解推导出整个问题的最优解,那么这种问题就不具有最优子结构。 +如果原问题的最优解可以由子问题的最优解推导出来,则说明满足最优子结构;反之,则不满足,不能用贪心算法。 -### 1.3 贪心算法正确性的证明 +### 1.3 贪心算法正确性简述 -贪心算法最难的部分不在于问题的求解,而在于是正确性的证明。我们常用的证明方法有「数学归纳法」和「交换论证法」。 +贪心算法的难点在于如何证明其选择策略能得到全局最优解。常见的两种证明方法: -> - **数学归纳法**:先计算出边界情况(例如 $n = 1$)的最优解,然后再证明对于每个 $n,ドル$F_{n + 1}$ 都可以由 $F_n$ 推导出。 -> -> - **交换论证法**:从最优解出发,在保证全局最优不变的前提下,如果交换方案中任意两个元素 / 相邻的两个元素后,答案不会变得更好,则可以推定目前的解是最优解。 +> - **数学归纳法**:先验证最小规模(如 $n = 1$)时成立,再证明 $n$ 成立时 $n + 1$ 也成立。 +> - **交换论证法**:假设存在更优解,通过交换局部选择,如果不会得到更优结果,则当前贪心解为最优。 -判断一个问题是否通过贪心算法求解,是需要进行严格的数学证明的。但是在日常写题或者算法面试中,不太会要求大家去证明贪心算法的正确性。 +实际刷题或面试时,通常不要求严格证明。判断是否可用贪心算法,可以通过: -所以,当我们想要判断一个问题是否通过贪心算法求解时,我们可以: +1. **直觉尝试**:先用贪心思路做一遍,看看局部最优能否推出全局最优。 +2. **举反例**:尝试构造反例,如果找不到局部最优导致全局最优失败的例子,基本可以用贪心法。 -1. **凭直觉**:如果感觉这道题可以通过「贪心算法」去做,就尝试找到局部最优解,再推导出全局最优解。 -2. **举反例**:尝试一下,举出反例。也就是说找出一个局部最优解推不出全局最优解的例子,或者找出一个替换当前子问题的最优解,可以得到更优解的例子。如果举不出反例,大概率这道题是可以通过贪心算法求解的。 +## 2. 贪心算法三步走 -## 3. 贪心算法三步走 +1. **问题转化**:将原始优化问题转化为可以应用贪心策略的问题,明确每一步都可以做出一个局部最优的选择。 +2. **贪心策略制定**:结合题意,选定合适的度量标准,设计出每一步的贪心选择规则,即在当前状态下选择最优(最有利)的方案,获得局部最优解。 +3. **最优子结构利用**:保证每次贪心选择后,剩余子问题仍满足同样的结构和贪心选择性质,将每一步的局部最优解累积,最终合成原问题的全局最优解。 -1. **转换问题**:将优化问题转换为具有贪心选择性质的问题,即先做出选择,再解决剩下的一个子问题。 -2. **贪心选择性质**:根据题意选择一种度量标准,制定贪心策略,选取当前状态下「最好 / 最优选择」,从而得到局部最优解。 -3. **最优子结构性质**:根据上一步制定的贪心策略,将贪心选择的局部最优解和子问题的最优解合并起来,得到原问题的最优解。 +## 3. 贪心算法的应用 -## 4. 贪心算法的应用 +### 3.1 经典例题:分发饼干 -### 4.1 分发饼干 - -#### 4.1.1 题目链接 +#### 3.1.1 题目链接 - [455. 分发饼干 - 力扣](https://leetcode.cn/problems/assign-cookies/) -#### 4.1.2 题目大意 +#### 3.1.2 题目大意 **描述**:一位很棒的家长为孩子们分发饼干。对于每个孩子 $i,ドル都有一个胃口值 $g[i],ドル即每个小孩希望得到饼干的最小尺寸值。对于每块饼干 $j,ドル都有一个尺寸值 $s[j]$。只有当 $s[j]> g[i]$ 时,我们才能将饼干 $j$ 分配给孩子 $i$。每个孩子最多只能给一块饼干。 @@ -104,46 +95,49 @@ 解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1, 2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出 2。 ``` -#### 4.1.3 解题思路 +#### 3.1.3 解题思路 ##### 思路 1:贪心算法 -为了尽可能的满足更多的小孩,而且一块饼干不能掰成两半,所以我们应该尽量让胃口小的孩子吃小块饼干,这样胃口大的孩子才有大块饼干吃。 +为了让尽可能多的孩子得到满足,且每块饼干只能分配给一个孩子,我们应优先用小尺寸的饼干满足胃口较小的孩子,将大尺寸的饼干留给胃口较大的孩子。 -所以,从贪心算法的角度来考虑,我们应该按照孩子的胃口从小到大对数组 $g$ 进行排序,然后按照饼干的尺寸大小从小到大对数组 $s$ 进行排序,并且对于每个孩子,应该选择满足这个孩子的胃口且尺寸最小的饼干。 +基于贪心思想,具体做法如下:先将孩子的胃口数组 $g$ 和饼干尺寸数组 $s$ 分别从小到大排序。然后,依次为每个孩子分配能够满足其胃口的最小尺寸饼干。 -下面我们使用贪心算法三步走的方法解决这道题。 +结合贪心算法的三步走: -1. **转换问题**:将原问题转变为,当胃口最小的孩子选择完满足这个孩子的胃口且尺寸最小的饼干之后,再解决剩下孩子的选择问题(子问题)。 -2. **贪心选择性质**:对于当前孩子,用尺寸尽可能小的饼干满足这个孩子的胃口。 -3. **最优子结构性质**:在上面的贪心策略下,当前孩子的贪心选择 + 剩下孩子的子问题最优解,就是全局最优解。也就是说在贪心选择的方案下,能够使得满足胃口的孩子数量达到最大。 +1. **问题转化**:将原问题转化为:每次优先用最小的饼干满足胃口最小的孩子,剩下的孩子和饼干继续按同样方式处理(即递归到子问题)。 +2. **贪心选择性质**:对于当前孩子,选择能满足其胃口的最小饼干。 +3. **最优子结构**:当前的贪心选择加上剩余子问题的最优解,能够保证全局最优,即最大化被满足的孩子数量。 -使用贪心算法的代码解决步骤描述如下: +具体实现步骤如下: -1. 对数组 $g$、$s$ 进行从小到大排序,使用变量 $index\_g$ 和 $index\_s$ 分别指向 $g$、$s$ 初始位置,使用变量 $res$ 保存结果,初始化为 0ドル$。 -2. 对比每个元素 $g[index\_g]$ 和 $s[index\_s]$: - 1. 如果 $g[index\_g] \le s[index\_s],ドル说明当前饼干满足当前孩子胃口,则答案数量加 1ドル,ドル并且向右移动 $index\_g$ 和 $index\_s$。 - 2. 如果 $g[index\_g]> s[index\_s],ドル说明当前饼干无法满足当前孩子胃口,则向右移动 $index_s,ドル判断下一块饼干是否可以满足当前孩子胃口。 -3. 遍历完输出答案 $res$。 +1. 对 $g$ 和 $s$ 升序排序,定义指针 $index\_g$ 和 $index\_s$ 分别指向 $g$ 和 $s$ 的起始位置,结果计数 $res$ 初始化为 0ドル$。 +2. 遍历两个数组,比较 $g[index\_g]$ 和 $s[index\_s]$: + 1. 如果 $g[index\_g] \le s[index\_s],ドル说明当前饼干可以满足当前孩子,$res$ 加 1ドル,ドル$index\_g$ 和 $index\_s$ 同时右移。 + 2. 如果 $g[index\_g]> s[index\_s],ドル说明当前饼干无法满足当前孩子,$index\_s$ 右移,尝试下一块饼干。 +3. 遍历结束后,输出 $res$ 即为最多能满足的孩子数量。 ##### 思路 1:代码 ```python class Solution: def findContentChildren(self, g: List[int], s: List[int]) -> int: + # 对孩子的胃口值和饼干尺寸进行升序排序 g.sort() s.sort() - index_g, index_s = 0, 0 - res = 0 + index_g, index_s = 0, 0 # index_g 指向当前要分配的孩子,index_s 指向当前可用的饼干 + res = 0 # 记录能满足的孩子数量 + # 遍历两个数组,直到有一个数组遍历完 while index_g < len(g) and index_s < len(s): + # 如果当前饼干可以满足当前孩子 if g[index_g] <= s[index_s]: - res += 1 - index_g += 1 - index_s += 1 + res += 1 # 满足的孩子数加一 + index_g += 1 # 指向下一个孩子 + index_s += 1 # 指向下一个饼干 else: - index_s += 1 + index_s += 1 # 当前饼干太小,尝试下一块饼干 - return res + return res # 返回最多能满足的孩子数量 ``` ##### 思路 1:复杂度分析 @@ -151,13 +145,13 @@ class Solution: - **时间复杂度**:$O(m \times \log m + n \times \log n),ドル其中 $m$ 和 $n$ 分别是数组 $g$ 和 $s$ 的长度。 - **空间复杂度**:$O(\log m + \log n)$。 -### 4.2 无重叠区间 +### 3.2 经典例题:无重叠区间 -#### 4.2.1 题目链接 +#### 3.2.1 题目链接 - [435. 无重叠区间 - 力扣](https://leetcode.cn/problems/non-overlapping-intervals/) -#### 4.2.2 题目大意 +#### 3.2.2 题目大意 **描述**:给定一个区间的集合 $intervals,ドル其中 $intervals[i] = [starti, endi]$。从集合中移除部分区间,使得剩下的区间互不重叠。 @@ -187,42 +181,50 @@ class Solution: 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。 ``` -#### 4.2.3 解题思路 +#### 3.2.3 解题思路 ##### 思路 1:贪心算法 -这道题我们可以转换一下思路。原题要求保证移除区间最少,使得剩下的区间互不重叠。换个角度就是:「如何使得剩下互不重叠区间的数目最多」。那么答案就变为了:「总区间个数 - 不重叠区间的最多个数」。我们的问题也变成了求所有区间中不重叠区间的最多个数。 +本题可以通过转换思路来简化求解。原题要求移除最少数量的区间,使得剩余区间互不重叠。换句话说,就是要让剩下的互不重叠区间数量最多。因此,答案等价于「总区间数 - 最多不重叠区间数」。问题转化为:在所有区间中,最多能选出多少个互不重叠的区间。 -从贪心算法的角度来考虑,我们应该将区间按照结束时间排序。每次选择结束时间最早的区间,然后再在剩下的时间内选出最多的区间。 +采用贪心算法时,核心策略是将区间按结束时间从小到大排序。每次总是选择结束时间最早且不与已选区间重叠的区间,这样可以在后续留出更多空间,选出更多区间。 -我们用贪心三部曲来解决这道题。 +具体贪心解题步骤如下: -1. **转换问题**:将原问题转变为,当选择结束时间最早的区间之后,再在剩下的时间内选出最多的区间(子问题)。 -2. **贪心选择性质**:每次选择时,选择结束时间最早的区间。这样选出来的区间一定是原问题最优解的区间之一。 -3. **最优子结构性质**:在上面的贪心策略下,贪心选择当前时间最早的区间 + 剩下的时间内选出最多区间的子问题最优解,就是全局最优解。也就是说在贪心选择的方案下,能够使所有区间中不重叠区间的个数最多。 +1. **问题转化**:将原问题转化为「选出最多不重叠区间」。 +2. **贪心选择性质**:每次总是选择当前结束时间最早且不与已选区间重叠的区间。 +3. **最优子结构性质**:当前选择加上后续子问题的最优解,能够得到全局最优解。 -使用贪心算法的代码解决步骤描述如下: +实现流程如下: -1. 将区间集合按照结束坐标升序排列,然后维护两个变量,一个是当前不重叠区间的结束时间 $end\_pos,ドル另一个是不重叠区间的个数 $count$。初始情况下,结束坐标 $end\_pos$ 为第一个区间的结束坐标,$count$ 为 1ドル$。 -2. 依次遍历每段区间。对于每段区间:$intervals[i]$: - 1. 如果 $end\_pos \le intervals[i][0],ドル即 $end\_pos$ 小于等于区间起始位置,则说明出现了不重叠区间,令不重叠区间数 $count$ 加 1ドル,ドル$end\_pos$ 更新为新区间的结束位置。 -3. 最终返回「总区间个数 - 不重叠区间的最多个数」即 $len(intervals) - count$ 作为答案。 +1. 先将所有区间按结束坐标升序排序。 +2. 维护两个变量:$end\_pos$ 表示当前已选区间的结束位置,$count$ 表示已选的不重叠区间数量。初始时,$end\_pos$ 取第一个区间的结束位置,$count=1$。 +3. 遍历后续区间,对于每个区间 $intervals[i]$: + - 若 $end\_pos \le intervals[i][0],ドル说明该区间与前面已选区间不重叠,则计数 $count+1,ドル并更新 $end\_pos$ 为当前区间的结束位置。 +4. 最终返回 $len(intervals) - count,ドル即最少需要移除的区间数。 ##### 思路 1:代码 ```python class Solution: def eraseOverlapIntervals(self, intervals: List[List[int]]) -> int: + # 如果区间列表为空,直接返回 0 if not intervals: return 0 + # 按区间的结束位置从小到大排序 intervals.sort(key=lambda x: x[1]) + # 初始化第一个区间的结束位置 end_pos = intervals[0][1] + # 记录不重叠区间的数量,初始为 1(第一个区间) count = 1 + # 遍历后续区间 for i in range(1, len(intervals)): + # 如果当前区间的起始位置不小于上一个已选区间的结束位置,说明不重叠 if end_pos <= intervals[i][0]: - count += 1 - end_pos = intervals[i][1] + count += 1 # 计数加一 + end_pos = intervals[i][1] # 更新当前已选区间的结束位置 + # 总区间数减去最多不重叠区间数,即为最少需要移除的区间数 return len(intervals) - count ``` @@ -231,6 +233,17 @@ class Solution: - **时间复杂度**:$O(n \times \log n),ドル其中 $n$ 是区间的数量。 - **空间复杂度**:$O(\log n)$。 +## 4. 总结 + +贪心算法是一种简单而有效的算法设计策略,其核心思想是在每一步都做出当前看起来最优的选择,期望通过一系列局部最优选择最终获得全局最优解。这种算法特别适用于具有贪心选择性质和最优子结构性质的问题。 + +贪心算法的优势在于其简洁性和高效性。相比动态规划需要存储和计算所有子问题的解,贪心算法只需要关注当前步骤的最优选择,大大降低了时间和空间复杂度。同时,贪心算法的实现通常比较简单直观,容易理解和编码。 + +然而,贪心算法也有其局限性。并非所有问题都适合使用贪心策略,只有同时满足贪心选择性质和最优子结构性质的问题才能保证得到全局最优解。对于不满足这些条件的问题,贪心算法可能只能得到局部最优解或近似解。此外,贪心算法的正确性证明往往比较复杂,需要严格的数学证明。 + +在实际应用中,贪心算法广泛应用于调度问题、图论问题、优化问题等领域。通过合理设计贪心策略,可以在保证解的质量的同时,显著提高算法的执行效率。掌握贪心算法的关键在于理解其适用条件,学会识别问题特征,并能够设计出合适的贪心选择策略。 + + ## 练习题目 - [0455. 分发饼干](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0400-0499/assign-cookies.md) diff --git a/docs/07_algorithm/07_06_bit_operation.md b/docs/07_algorithm/07_06_bit_operation.md index 52bd9791..968b933a 100644 --- a/docs/07_algorithm/07_06_bit_operation.md +++ b/docs/07_algorithm/07_06_bit_operation.md @@ -1,180 +1,180 @@ ## 1. 位运算简介 -### 1.1 位运算与二进制简介 +### 1.1 位运算与二进制基础 -> **位运算(Bit Operation)**:在计算机内部,数是以「二进制(Binary)」的形式来进行存储。位运算就是直接对数的二进制进行计算操作,在程序中使用位运算进行操作,会大大提高程序的性能。 +> **位运算(Bit Operation)**:计算机内部所有数据均以「二进制(Binary)」形式存储。位运算是直接对二进制位进行操作的运算方式,能够极大提升程序的执行效率。 -在学习二进制数的位运算之前,我们先来了解一下什么叫做「二进制数」。 +在正式学习位运算之前,先简单了解「二进制数」的基本概念。 ![二进制数](https://qcdn.itcharge.cn/images/202405132135165.png) -> **二进制数(Binary)**:由 0ドル$ 和 1ドル$ 两个数码来表示的数。二进制数中每一个 0ドル$ 或每一个 1ドル$ 都称为一个「位(Bit)」。 +> **二进制数(Binary)**:仅由 0ドル$ 和 1ドル$ 两个数字组成。二进制数中的每一位(0ドル$ 或 1ドル$)称为一个「位(Bit)」。 -我们通常使用的十进制数有 0ドル \sim 9$ 共 10ドル$ 个数字,进位规则是「满十进一」。例如: +我们日常使用的十进制数包含 0ドル \sim 9$ 共 10ドル$ 个数字,进位规则为「满十进一」。例如: -1. 7ドル_{(10)} + 2_{(10)} = 9_{(10)}$:7ドル_{(10)}$ 加上 2ドル_{(10)}$ 等于 9ドル_{(10)}$。 -2. 9ドル_{(10)} + 2_{(10)} = 11_{(10)}$:9ドル_{(10)}$ 加上 2ドル_{(10)}$ 之后个位大于等于 10ドル,ドル符合「满十进一」,结果等于 11ドル_{(10)}$。 +1. 7ドル_{(10)} + 2_{(10)} = 9_{(10)}$:7ドル_{(10)}$ 加 2ドル_{(10)}$ 得 9ドル_{(10)}$。 +2. 9ドル_{(10)} + 2_{(10)} = 11_{(10)}$:9ドル_{(10)}$ 加 2ドル_{(10)}$ 后个位满 10ドル$ 进一,结果为 11ドル_{(10)}$。 -而在二进制数中,我们只有 0ドル$ 和 1ドル$ 两个数码,它的进位规则是「逢二进一」。例如: +而二进制数仅有 0ドル$ 和 1ドル,ドル进位规则为「逢二进一」。例如: -1. 1ドル_{(2)} + 0_{(2)} = 1_{(2)}$:1ドル_{(2)}$ 加上 0ドル_{(2)}$ 等于 1ドル_{(2)}$。 -2. 1ドル_{(2)} + 1_{(2)} = 10_{(2)}$:1ドル_{(2)}$ 加上 1ドル_{(2)},ドル大于等于 2ドル,ドル符合「逢二进一」,结果等于 10ドル_{(2)}$。 -3. 10ドル_{(2)} + 1_{(2)} = 11_{(2)}$。 +1. 1ドル_{(2)} + 0_{(2)} = 1_{(2)}$:1ドル_{(2)}$ 加 0ドル_{(2)}$ 得 1ドル_{(2)}$。 +2. 1ドル_{(2)} + 1_{(2)} = 10_{(2)}$:1ドル_{(2)}$ 加 1ドル_{(2)},ドル满 2ドル$ 进一,结果为 10ドル_{(2)}$。 +3. 10ドル_{(2)} + 1_{(2)} = 11_{(2)}$:10ドル_{(2)}$ 加 1ドル_{(2)}$ 得 11ドル_{(2)}$。 -### 1.2 二进制数的转换 +### 1.2 二进制与十进制的相互转换 -#### 1.2.1 二进制转十进制数 +#### 1.2.1 二进制转十进制 -在十进制数中,数字 2749ドル_{(10)}$ 可以理解为 2ドル \times 1000 + 7 \times 100 + 4 \times 10 + 9 * 1,ドル相当于 2ドル \times 10^3 + 7 \times 10^2 + 4 \times 10^1 + 9 \times 10^0,ドル即 2000ドル + 700 +たす 40 +たす 9 =わ 2749_{(10)}$。 +将二进制数转为十进制,就是将每一位上的数字乘以对应的 2ドル$ 的幂次,然后相加。例如:十进制 2749ドル_{(10)}$ 展开为 2ドル \times 10^3 + 7 \times 10^2 + 4 \times 10^1 + 9 \times 10^0 = 2000 +たす 700 +たす 40 +たす 9 =わ 2749$。 -同理,在二进制数中,01101010ドル_{(2)}$ 可以看作为 $(0 \times 2^7) + (1 \times 2^6) + (1 \times 2^5) + (0 \times 2^4) + (1 \times 2^3) + (0 \times 2^2) + (1 \times 2^1) + (0 \times 2^0),ドル即 0ドル + 64 +たす 32 +たす 0 +たす 8 +たす 0 +たす 2 +たす 0 =わ 106_{(10)}$。 + +同理,在二进制数中,01101010ドル_{(2)}$ 展开为 0ドル \times 2^7 + 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 0 + 64 +たす 32 +たす 0 +たす 8 +たす 0 +たす 2 +たす 0 =わ 106_{(10)}$。 ![二进制数转十进制数](https://qcdn.itcharge.cn/images/202405132136456.png) 我们可以通过这样的方式,将一个二进制数转为十进制数。 -#### 1.2.2 十进制转二进制数 +#### 1.2.2 十进制转二进制 + +十进制转二进制常用方法是「除2取余,逆序排列」。 -十进制数转二进制数的方法是:**除二取余,逆序排列法**。 +以 106ドル_{(10)}$ 为例: -我们以十进制数中的 106ドル_{(10)}$ 为例。 +1. 106ドル \div 2 = 53,ドル余 0ドル$。 +2. 53ドル \div 2 = 26,ドル余 1ドル$。 +3. 26ドル \div 2 = 13,ドル余 0ドル$。 +4. 13ドル \div 2 = 6,ドル余 1ドル$。 +5. 6ドル \div 2 = 3,ドル余 0ドル$。 +6. 3ドル \div 2 = 1,ドル余 1ドル$。 +7. 1ドル \div 2 = 0,ドル余 1ドル$。 +8. 0ドル \div 2 = 0,ドル余 0ドル$。 -$\begin{aligned} 106 \div 2 = 53 & \text{(余 0)} \cr 53 \div 2 = 26 & \text{(余 1)} \cr 26 \div 2 = 13 & \text{(余 0)} \cr 13 \div 2 = 6 & \text{(余 1)} \cr 6 \div 2 = 3 & \text{(余 0)} \cr 3 \div 2 = 1 & \text{(余 1)} \cr 1 \div 2 = 0 & \text{(余 1)} \cr 0 \div 2 = 0 & \text{(余 0)} \end{aligned}$ +将余数逆序排列,得到 01101010ドル_{(2)}$。 -我们反向遍历每次计算的余数,依次是 0ドル,ドル1ドル,ドル1ドル,ドル0ドル,ドル1ドル,ドル0ドル,ドル1ドル,ドル0ドル,ドル即 01101010ドル_{(2)}$。 +简而言之:**不断除以 2,记录余数,最后将余数逆序排列即可得到二进制表示。** ## 2. 位运算基础操作 -在二进制的基础上,我们可以对二进制数进行相应的位运算。基本的位运算共有 6ドル$ 种,分别是:「按位与运算」、「按位或运算」、「按位异或运算」、「取反运算」、「左移运算」、「右移运算」。 +基于二进制表示,我们可以对数字进行多种位运算。常见的位运算包括 6ドル$ 种:「按位与」、「按位或」、「按位异或」、「取反」、「左移」和「右移」。 -这里的「按位与运算」、「按位或运算」、「按位异或运算」、「左移运算」、「右移运算」是双目运算。 +其中,「按位与」、「按位或」、「按位异或」、「左移」、「右移」属于双目运算(需要两个操作数): -- 「按位与运算」、「按位或运算」、「按位异或运算」是将两个整数作为二进制数,对二进制数表示中的每一位(即二进位)逐一进行相应运算,即双目运算。 -- 「左移运算」、「右移运算」是将左侧整数作为二进制数,将右侧整数作为移动位数,然后对左侧二进制数的全部位进行移位运算,每次移动一位,总共移动右侧整数次位,也是双目运算。 +- 「按位与」、「按位或」、「按位异或」:将两个整数转为二进制后,对应位逐一进行运算。 +- 「左移」、「右移」:左侧为待移位的整数,右侧为移动的位数,对左侧二进制的所有位整体移动指定次数。 -而「取反运算」是单目运算,是对一个整数的二进制数进行的位运算。 +「取反」属于单目运算(只需一个操作数),即对一个整数的每一位进行取反操作。 -我们先来看下这 6ドル$ 种位运算的规则,再来进行详细讲解。 +下面先简要介绍这 6ドル$ 种位运算的基本规则,后续将逐一详细讲解。 -| 运算符 | 描述 | 规则 | -| ------------------- | -------------- | ----------------------------------------------------------------------------------------- | -| | | 按位或运算符 | 只要对应的两个二进位有一个为 1ドル$ 时,结果位就为 1ドル$。 | -| `&` | 按位与运算符 | 只有对应的两个二进位都为 1ドル$ 时,结果位才为 1ドル$。 | -| `<<` | 左移运算符 | 将二进制数的各个二进位全部左移若干位。`<<` 右侧数字指定了移动位数,高位丢弃,低位补 0ドル$。 | -| `>>` | 右移运算符 | 对二进制数的各个二进位全部右移若干位。`>>` 右侧数字指定了移动位数,低位丢弃,高位补 0ドル$。 | -| `^` | 按位异或运算符 | 对应的两个二进位相异时,结果位为 1ドル,ドル二进位相同时则结果位为 0ドル$。 | -| `~` | 取反运算符 | 对二进制数的每个二进位取反,使数字 1ドル$ 变为 0ドル,ドル0ドル$ 变为 1ドル$。 | +| 运算符 | 描述 | 规则说明 | +| --------- | ------------ | --------------------------------------------------------------------------------------------- | +| | | 按位或 | 只要对应的两个二进位中有一个为 1ドル,ドル结果位即为 1ドル,ドル否则为 0ドル$。 | +| `&` | 按位与 | 仅当对应的两个二进位都为 1ドル$ 时,结果位才为 1ドル,ドル否则为 0ドル$。 | +| `^` | 按位异或 | 对应的两个二进位不同则结果位为 1ドル,ドル相同则为 0ドル$。 | +| `~` | 按位取反 | 对操作数的每一位取反,1ドル$ 变为 0ドル,ドル0ドル$ 变为 1ドル$。 | +| `<<` | 左移 | 所有二进位整体向左移动指定的位数,高位溢出丢弃,低位补 0ドル$。 | +| `>>` | 右移 | 所有二进位整体向右移动指定的位数,低位溢出丢弃,高位补 0ドル$(无符号右移时)。 | ### 2.1 按位与运算 -> **按位与运算(AND)**:按位与运算符为 `&`。其功能是对两个二进制数的每一个二进位进行与运算。 - -- **按位与运算规则**:只有对应的两个二进位都为 1ドル$ 时,结果位才为 1ドル$。 +> **按位与运算(AND)**:使用运算符 `&`,对两个二进制数的每一位进行比较,只有当对应位都为 1ドル$ 时,结果位才为 1ドル,ドル否则为 0ドル$。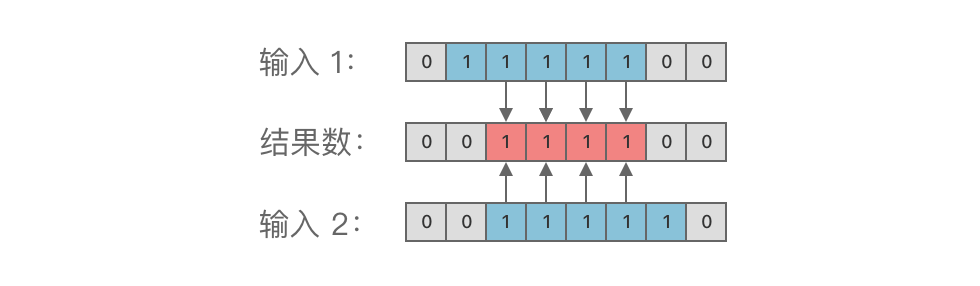 +- **按位与运算规则**: - `1 & 1 = 1` - - `1 & 0 = 0` - - `0 & 1 = 0` - - `0 & 0 = 0` - -举个例子,对二进制数 01111100ドル_{(2)}$ 与 00111110ドル_{(2)}$ 进行按位与运算,结果为 00111100ドル_{(2)},ドル如图所示: +例如,将 01111100ドル_{(2)}$ 与 00111110ドル_{(2)}$ 进行按位与运算,结果为 00111100ドル_{(2)},ドル如下图所示: ![按位与运算](https://qcdn.itcharge.cn/images/202405132137023.png) ### 2.2 按位或运算 -> **按位或运算(OR)**:按位或运算符为 `|`。其功能对两个二进制数的每一个二进位进行或运算。 +> **按位或运算(OR)**:使用运算符 `|`,对两个二进制数的每一位进行「或」操作。只要对应的两个二进位中有一个为 1ドル,ドル结果位就是 1ドル,ドル只有两个都是 0ドル$ 时结果才为 0ドル$。 -- **按位或运算规则**:只要对应的两个二进位有一个为 1ドル$ 时,结果位就为 1ドル$。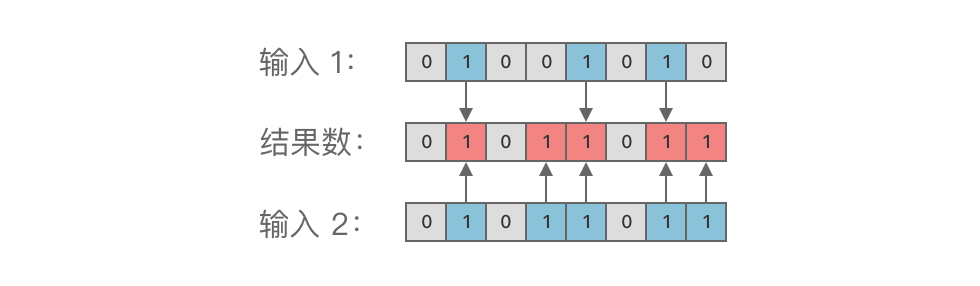 +- **按位或运算规则**: - `1 | 1 = 1` - `1 | 0 = 1` - `0 | 1 = 1` - `0 | 0 = 0` - -举个例子,对二进制数 01001010ドル_{(2)}$ 与 01011011ドル_{(2)}$ 进行按位或运算,结果为 01011011ドル_{(2)},ドル如图所示: +例如,将 01001010ドル_{(2)}$ 与 01011011ドル_{(2)}$ 进行按位或运算,结果为 01011011ドル_{(2)},ドル如下图所示: ![按位或运算](https://qcdn.itcharge.cn/images/202405132137593.png) ### 2.3 按位异或运算 -> **按位异或运算(XOR)**:按位异或运算符为 `^`。其功能是对两个二进制数的每一个二进位进行异或运算。 +> **按位异或运算(XOR)**:使用运算符 `^`,对两个二进制数的每一位进行比较。只有当对应的两位不同(即一位为 1ドル,ドル一位为 0ドル$)时,结果位才为 1ドル,ドル否则为 0ドル$。 -- **按位异或运算规则**:对应的两个二进位相异时,结果位为 1ドル,ドル二进位相同时则结果位为 0ドル$。 -- `0 ^ 0 = 0` - -- `1 ^ 0 = 1` - -- `0 ^ 1 = 1` - -- `1 ^ 1 = 0` +- **按位异或运算运算规则**: + - `0 ^ 0 = 0` + - `1 ^ 0 = 1` + - `0 ^ 1 = 1` + - `1 ^ 1 = 0` +简而言之,异或运算的本质是「相同为 0ドル,ドル不同为 1ドル$」。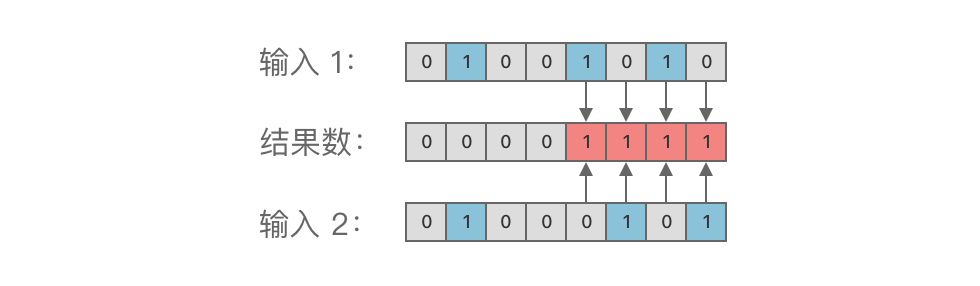 -举个例子,对二进制数 01001010ドル_{(2)}$ 与 01000101ドル_{(2)}$ 进行按位异或运算,结果为 00001111ドル_{(2)},ドル如图所示: +例如,将 01001010ドル_{(2)}$ 与 01000101ドル_{(2)}$ 进行按位异或运算,结果为 00001111ドル_{(2)},ドル如下图所示: ![按位异或运算](https://qcdn.itcharge.cn/images/202405132137874.png) ### 2.4 取反运算 ->**取反运算(NOT)**:取反运算符为 `~`。其功能是对一个二进制数的每一个二进位进行取反运算。 +> **取反运算(NOT)**:取反运算符为 `~`,用于将一个二进制数的每一位进行翻转,即 1ドル$ 变为 0ドル,ドル0ドル$ 变为 1ドル$。 -- **取反运算规则**:使数字 1ドル$ 变为 0ドル,ドル0ドル$ 变为 1ドル$。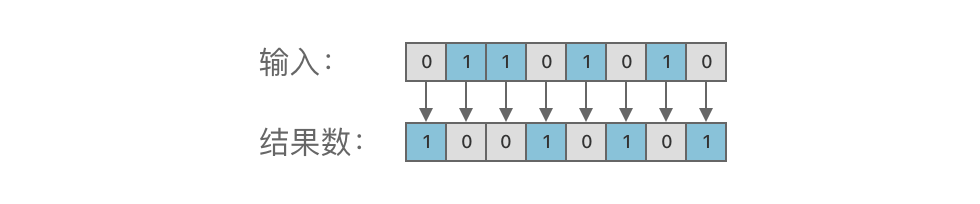 +- **取反运算规则**: - `~0 = 1` - `~1 = 0` -举个例子,对二进制数 01101010ドル_{(2)}$ 进行取反运算,结果如图所示: +例如,对二进制数 01101010ドル_{(2)}$ 进行取反,结果如下图所示: ![取反运算](https://qcdn.itcharge.cn/images/202405132138853.png) -### 2.5 左移运算和右移运算 +### 2.5 左移运算与右移运算 -> **左移运算(SHL)**: 左移运算符为 `<<`。其功能是对一个二进制数的各个二进位全部左移若干位(高位丢弃,低位补 0ドル$)。 +> **左移运算(SHL)**:使用运算符 `<<`,将一个二进制数的所有位整体向左移动指定的位数。左移时,高位超出部分被舍弃,低位空缺部分补 0ドル$。 -举个例子,对二进制数 01101010ドル_{(2)}$ 进行左移 1ドル$ 位运算,结果为 11010100ドル_{(2)},ドル如图所示: +例如,将二进制数 01101010ドル_{(2)}$ 左移 1ドル$ 位,得到 11010100ドル_{(2)},ドル如下图所示: 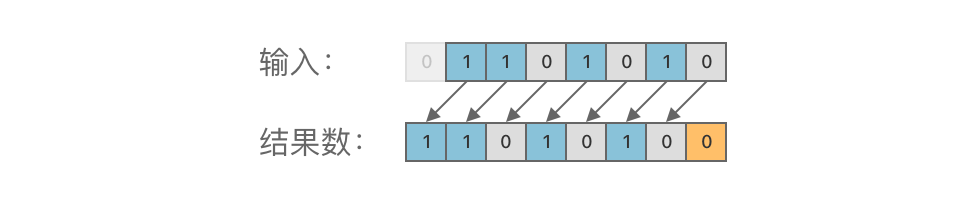![左移运算](https://qcdn.itcharge.cn/images/202405132138841.png) -> **右移运算(SHR)**: 右移运算符为 `>>`。其功能是对一个二进制数的各个二进位全部右移若干位(低位丢弃,高位补 0ドル$)。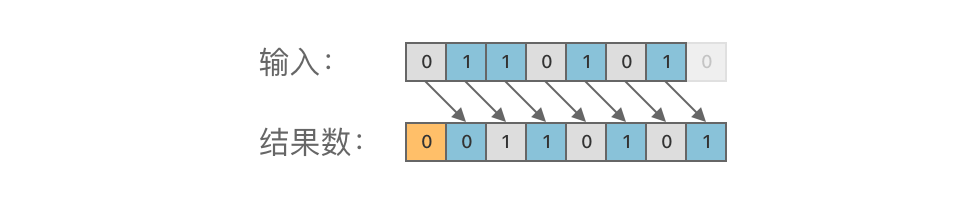 +> **右移运算(SHR)**:使用运算符 `>>`,将一个二进制数的所有位整体向右移动指定的位数。右移时,低位超出部分被舍弃,高位空缺部分补 0ドル$。 -举个例子,对二进制数 01101010ドル_{(2)}$ 进行右移 1ドル$ 位运算,结果为 00110101ドル_{(2)},ドル如图所示: +例如,将二进制数 01101010ドル_{(2)}$ 右移 1ドル$ 位,得到 00110101ドル_{(2)},ドル如下图所示: ![右移运算](https://qcdn.itcharge.cn/images/202405132138348.png) ## 3. 位运算的应用 -### 3.1 位运算的常用操作 - -#### 3.1.1 判断整数奇偶 +### 3.1 判断整数奇偶 -一个整数,只要是偶数,其对应二进制数的末尾一定为 0ドル$;只要是奇数,其对应二进制数的末尾一定为 1ドル$。所以,我们通过与 1ドル$ 进行按位与运算,即可判断某个数是奇数还是偶数。 +判断一个整数的奇偶性,可以利用其二进制表示的最低位。偶数的二进制最低位为 0ドル,ドル奇数的最低位为 1ドル$。因此,通过将该数与 1ドル$ 进行按位与运算即可快速判断: -1. `(x & 1) == 0` 为偶数。 -2. `(x & 1) == 1` 为奇数。 +- 如果 `(x & 1) == 0`,则 $x$ 为偶数; +- 如果 `(x & 1) == 1`,则 $x$ 为奇数。 -#### 3.1.2 二进制数选取指定位 +### 3.2 二进制数选取指定位 -如果我们想要从一个二进制数 $X$ 中取出某几位,使取出位置上的二进位保留原值,其余位置为 0ドル,ドル则可以使用另一个二进制数 $Y,ドル使该二进制数上对应取出位置为 1ドル,ドル其余位置为 0ドル$。然后令两个数进行按位与运算(`X & Y`),即可得到想要的数。 +若需从二进制数 $X$ 中提取指定的若干位(即保留这些位的原值,其余位置为 0ドル$),可以先构造一个掩码 $Y,ドル使得需要保留的位置为 1ドル,ドル其余为 0ドル$。随后通过按位与运算(`X & Y`)即可实现目标。 -举个例子,比如我们要取二进制数 $X = 01101010_{(2)}$ 的末尾 4ドル$ 位,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$ (末尾 4ドル$ 位为 1ドル,ドル其余位为 0ドル$) 进行按位与运算,即 `01101010 & 00001111 == 00001010`。其结果 00001010ドル$ 就是我们想要的数(即二进制数 01101010ドル_{(2)}$ 的末尾 4ドル$ 位)。 +例如,如果要获取 $X = 01101010_{(2)}$ 的最低 4ドル$ 位,只需将其与 $Y = 00001111_{(2)}$(最低 4ドル$ 位为 1ドル,ドル其余为 0ドル$)进行按位与运算:`01101010 & 00001111 = 00001010`。结果 00001010ドル$ 即为 $X$ 的末尾 4ドル$ 位。 -#### 3.1.3 将指定位设置为 1ドル$ +### 3.3 将指定位设置为 1ドル$ -如果我们想要把一个二进制数 $X$ 中的某几位设置为 1ドル,ドル其余位置保留原值,则可以使用另一个二进制数 $Y,ドル使得该二进制上对应选取位置为 1ドル,ドル其余位置为 0ドル$。然后令两个数进行按位或运算(`X | Y`),即可得到想要的数。 +若需将二进制数 $X$ 的某几位强制设置为 1ドル$(其余位保持原值),可构造一个掩码 $Y,ドル使得需要设置为 1ドル$ 的位为 1ドル,ドル其余为 0ドル$。然后通过按位或运算(`X | Y`)即可实现。 -举个例子,比如我们想要将二进制数 $X = 01101010_{(2)}$ 的末尾 4ドル$ 位设置为 1ドル,ドル其余位置保留原值,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$(末尾 4ドル$ 位为 1ドル,ドル其余位为 0ドル$)进行按位或运算,即 `01101010 | 00001111 = 01101111`。其结果 01101111ドル$ 就是我们想要的数(即将二进制数 01101010ドル_{(2)}$ 的末尾 4ドル$ 位设置为 1ドル,ドル其余位置保留原值)。 +例如,若要将 $X = 01101010_{(2)}$ 的最低 4ドル$ 位设置为 1ドル,ドル其余位不变,只需与 $Y = 00001111_{(2)}$(最低 4ドル$ 位为 1ドル,ドル其余为 0ドル$)进行按位或运算:`01101010 | 00001111 = 01101111`。结果 01101111ドル$ 即为所需的新数。 -#### 3.1.4 反转指定位 +### 3.4 反转指定位 -如果我们想要把一个二进制数 $X$ 的某几位进行反转,则可以使用另一个二进制数 $Y,ドル使得该二进制上对应选取位置为 1ドル,ドル其余位置为 0ドル$。然后令两个数进行按位异或运算(`X ^ Y`),即可得到想要的数。 +若需反转二进制数 $X$ 的某几位,可构造一个掩码 $Y,ドル使得需要反转的位置为 1ドル,ドル其余为 0ドル$。然后对 $X$ 和 $Y$ 进行按位异或运算(`X ^ Y`),即可实现指定位的反转。 -举个例子,比如想要将二进制数 $X = 01101010_{(2)}$ 的末尾 4ドル$ 位进行反转,则只需将 $X = 01101010_{(2)}$ 与 $Y = 00001111_{(2)}$(末尾 4ドル$ 位为 1ドル,ドル其余位为 0ドル$)进行按位异或运算,即 `01101010 ^ 00001111 = 01100101`。其结果 01100101ドル$ 就是我们想要的数(即将二进制数 $X = 01101010_{(2)}$ 的末尾 4ドル$ 位进行反转)。 +例如,若要反转 $X = 01101010_{(2)}$ 的最低 4ドル$ 位,只需将其与 $Y = 00001111_{(2)}$(最低 4ドル$ 位为 1ドル,ドル其余为 0ドル$)进行异或:`01101010 ^ 00001111 = 01100101`。结果 01100101ドル$ 即为 $X$ 的最低 4ドル$ 位被反转后的新值。 -#### 3.1.5 交换两个数 +### 3.5 交换两个数 -通过按位异或运算可以实现交换两个数的目的(只能用于交换两个整数)。 +通过按位异或运算,可以无需临时变量实现两个整数的交换(仅适用于整数类型)。示例代码如下: ```python a, b = 10, 20 @@ -184,17 +184,17 @@ a ^= b print(a, b) ``` -#### 3.1.6 将二进制最右侧为 1ドル$ 的二进位改为 0ドル$ +### 3.6 将二进制最右侧为 1ドル$ 的二进位改为 0ドル$ -如果我们想要将一个二进制数 $X$ 最右侧为 1ドル$ 的二进制位改为 0ドル,ドル则只需通过 `X & (X - 1)` 的操作即可完成。 +要将二进制数 $X$ 最右侧的 1ドル$ 置为 0ドル,ドル只需执行 `X & (X - 1)` 操作即可。 -比如 $X = 01101100_{(2)},ドル$X - 1 = 01101011_{(2)},ドル则 `X & (X - 1) == 01101100 & 01101011 =わ=わ 01101000`,结果为 01101000ドル_{(2)}$(即将 $X$ 最右侧为 1ドル$ 的二进制为改为 0ドル$)。 +例如,$X = 01101100_{(2)},ドル$X - 1 = 01101011_{(2)},ドル则 `X & (X - 1) = 01101100 & 01101011 =わ 01101000`,结果为 01101000ドル_{(2)},ドル即成功将 $X$ 最右侧的 1ドル$ 变为 0ドル$。 -#### 3.1.7 计算二进制中二进位为 1ドル$ 的个数 +### 3.7 计算二进制中二进位为 1ドル$ 的个数 -从 3.1.6 中得知,通过 `X & (X - 1)` 我们可以将二进制 $X$ 最右侧为 1ドル$ 的二进制位改为 0ドル,ドル那么如果我们不断通过 `X & (X - 1)` 操作,最终将二进制 $X$ 变为 0ドル,ドル并统计执行次数,则可以得到二进制中二进位为 1ドル$ 的个数。 +根据 3.6 节的内容,利用 `X & (X - 1)` 操作可以将二进制数 $X$ 的最右侧一个 1ドル$ 变为 0ドル$。因此,如果我们不断对 $X$ 执行该操作,直到 $X$ 变为 0ドル,ドル并统计操作次数,就能得到 $X$ 的二进制表示中 1ドル$ 的个数。 -具体代码如下: +实现代码如下: ```python class Solution: @@ -206,110 +206,113 @@ class Solution: return cnt ``` -#### 3.1.8 判断某数是否为 2ドル$ 的幂次方 +### 3.8 判断某数是否为 2ドル$ 的幂次方 -通过判断 `X & (X - 1) == 0` 是否成立,即可判断 $X$ 是否为 2ドル$ 的幂次方。 +判断一个数 $X$ 是否为 2ドル$ 的幂,可以利用位运算:只需判断 `X & (X - 1) == 0` 是否成立。 -这是因为: +原理如下: -1. 凡是 2ドル$ 的幂次方,其二进制数的某一高位为 1ドル,ドル并且仅此高位为 1ドル,ドル其余位都为 0ドル$。比如:4ドル_{(10)} = 00000100_{(2)}$、8ドル_{(10)} = 00001000_{(2)}$。 -2. 不是 2ドル$ 的幂次方,其二进制数存在多个值为 1ドル$ 的位。比如:5ドル_{10} = 00000101_{(2)}$、6ドル_{10} = 00000110_{(2)}$。 +- 如果 $X$ 是 2ドル$ 的幂,则其二进制表示只有一位为 1ドル,ドル其余全为 0ドル,ドル如 4ドル_{(10)} = 00000100_{(2)},ドル8ドル_{(10)} = 00001000_{(2)}$。 +- 如果 $X$ 不是 2ドル$ 的幂,则其二进制表示中有多位为 1ドル,ドル如 5ドル_{(10)} = 00000101_{(2)},ドル6ドル_{(10)} = 00000110_{(2)}$。 -接下来我们使用 `X & (X - 1)` 操作,将原数对应二进制数最右侧为 1ドル$ 的二进位改为 0ドル$ 之后,得到新值: +当 $X> 0$ 时,`X & (X - 1)` 的作用是将 $X$ 最右侧的 1ドル$ 变为 0ドル,ドル其余位保持不变: -1. 如果原数是 2ドル$ 的幂次方,则通过 `X & (X - 1)` 操作之后,新值所有位都为 0ドル,ドル值为 0ドル$。 -2. 如果该数不是 2ドル$ 的幂次方,则通过 `X & (X - 1)` 操作之后,新值仍存在不为 0ドル$ 的位,值肯定不为 0ドル$。 +- 如果 $X$ 是 2ドル$ 的幂,执行 `X & (X - 1)` 后结果为 0ドル$。 +- 如果 $X$ 不是 2ドル$ 的幂,执行后结果不为 0ドル$。 -所以我们可以通过是否为 0ドル$ 即可判断该数是否为 2ドル$ 的幂次方。 +因此,只需判断 `X> 0` 且 `X & (X - 1) == 0`,即可确定 $X$ 是否为 2ドル$ 的幂。 -### 3.2 位运算的常用操作总结 +### 3.9 位运算的常用操作总结 -| 功 能 | 位运算 | 示例 | -| ----------------------------------------- | ------------------------------------------------------- | ------------------------- | -| **从右边开始,把最后一个 1ドル$ 改写成 0ドル$** | x & (x - 1) | `100101000 -> 100100000` | -| **去掉右边起第一个 1ドル$ 的左边** | x & (x ^ (x - 1)) 或 x & (-x) | `100101000 -> 1000` | -| **去掉最后一位** | x >> 1 | `101101 -> 10110` | -| **取右数第 $k$ 位** | x >> (k - 1) & 1 | `1101101 -> 1, k = 4` | -| **取末尾 3ドル$ 位** | x & 7 | `1101101 -> 101` | -| **取末尾 $k$ 位** | x & 15 | `1101101 -> 1101, k = 4` | -| **只保留右边连续的 1ドル$** | (x ^ (x + 1)) >> 1 | `100101111 -> 1111` | -| **右数第 $k$ 位取反** | x ^ (1 << (k - 1)) | `101001 -> 101101, k = 3` | -| **在最后加一个 0ドル$** | x << 1 | `101101 -> 1011010` | -| **在最后加一个 1ドル$** | (x << 1) + 1 | `101101 -> 1011011` | -| **把右数第 $k$ 位变成 0ドル$** | x & ~(1 << (k - 1)) | `101101 -> 101001, k = 3` | -| **把右数第 $k$ 位变成 1ドル$** | x | (1 << (k - 1)) | `101001 -> 101101, k = 3` | -| **把右边起第一个 0ドル$ 变成 1ドル$** | x | (x + 1) | `100101111 -> 100111111` | -| **把右边连续的 0ドル$ 变成 1ドル$** | x | (x - 1) | `11011000 -> 11011111` | -| **把右边连续的 1ドル$ 变成 0ドル$** | x & (x + 1) | `100101111 -> 100100000` | -| **把最后一位变成 0ドル$** | x | 1 - 1 | `101101 -> 101100` | -| **把最后一位变成 1ドル$** | x | 1 | `101100 -> 101101` | -| **把末尾 $k$ 位变成 1ドル$** | x | (1 << k - 1) | `101001 -> 101111, k = 4` | -| **最后一位取反** | x ^ 1 | `101101 -> 101100` | -| **末尾 $k$ 位取反** | x ^ (1 << k - 1) | `101001 -> 100110, k = 4` | +| 序号 | 操作描述 | 位运算表达式 | 示例 | +| :--: | :--------------------------------------- | :------------------------------------- | :-------------------------- | +| 1 | 从右边开始,把最后一个 1ドル$ 改写成 0ドル$ | x & (x - 1) | `100101000 -> 100100000` | +| 2 | 保留最右侧的 1ドル,ドル其余清零 | x & -x 或 x & (x ^ (x - 1)) | `100101000 -> 1000` | +| 3 | 去掉最后一位 | x>> 1 | `101101 -> 10110` | +| 4 | 取右数第 $k$ 位 | (x>> (k - 1)) & 1 | `1101101 -> 1, k = 4` | +| 5 | 取末尾 $k$ 位 | x & ((1 << k) - 1) | `1101101 -> 101, k = 3`;
`1101101 -> 1101, k = 4` | +| 6 | 只保留右边连续的 1ドル$ | (x ^ (x + 1))>> 1 | `100101111 -> 1111` | +| 7 | 右数第 $k$ 位取反 | x ^ (1 << (k - 1)) | `101001 -> 101101, k = 3` | +| 8 | 在最后加一个 0ドル$ | x << 1 | `101101 -> 1011010` | +| 9 | 在最后加一个 1ドル$ | (x << 1) + 1 | `101101 -> 1011011` | +| 10 | 把右数第 $k$ 位变成 0ドル$ | x & ~(1 << (k - 1)) | `101101 -> 101001, k = 3` | +| 11 | 把右数第 $k$ 位变成 1ドル$ | x | (1 << (k - 1)) | `101001 -> 101101, k = 3` | +| 12 | 把右边起第一个 0ドル$ 变成 1ドル$ | x | (x + 1) | `100101111 -> 100111111` | +| 13 | 把右边连续的 0ドル$ 变成 1ドル$ | x | (x - 1) | `11011000 -> 11011111` | +| 14 | 把右边连续的 1ドル$ 变成 0ドル$ | x & (x + 1) | `100101111 -> 100100000` | +| 15 | 把最后一位变成 0ドル$ | x & ~1 | `101101 -> 101100` | +| 16 | 把最后一位变成 1ドル$ | x | 1 | `101100 -> 101101` | +| 17 | 把末尾 $k$ 位变成 1ドル$ | x | ((1 << k) - 1) | `101001 -> 101111, k = 4` | +| 18 | 末尾 $k$ 位取反 | x ^ ((1 << k) - 1) | `101101 -> 101100, k = 1`;
`101001 -> 100110, k = 4` | ### 3.3 二进制枚举子集 -除了上面的这些常见操作,我们经常常使用二进制数第 1ドル \sim n$ 位上 0ドル$ 或 1ドル$ 的状态来表示一个由 1ドル \sim n$ 组成的集合。也就是说通过二进制来枚举子集。 +在位运算中,常常利用二进制的第 1ドル \sim n$ 位上的 0ドル$ 或 1ドル$ 来表示由 1ドル \sim n$ 组成的集合,从而实现对子集的高效枚举。 #### 3.3.1 二进制枚举子集简介 -先来介绍一下「子集」的概念。 +首先,简要介绍一下「子集」的定义: -- **子集**:如果集合 $A$ 的任意一个元素都是集合 $S$ 的元素,则称集合 $A$ 是集合 $S$ 的子集。可以记为 $A \in S$。 +- **子集**:如果集合 $A$ 的所有元素均属于集合 $S,ドル则称 $A$ 是 $S$ 的子集,记作 $A \subseteq S$。 -有时候我们会遇到这样的问题:给定一个集合 $S,ドル枚举其所有可能的子集。 +实际问题中,常常需要枚举集合 $S$ 的所有子集。枚举子集的方法有多种,这里介绍一种简洁高效的方式:「二进制枚举子集」。 -枚举子集的方法有很多,这里介绍一种简单有效的枚举方法:「二进制枚举子集算法」。 +对于一个包含 $n$ 个元素的集合 $S,ドル每个元素都有「选」或「不选」两种状态。我们可以用二进制数的 $n$ 位来表示每个元素的选取情况:1ドル$ 表示选取该元素,0ドル$ 表示不选取。 -对于一个元素个数为 $n$ 的集合 $S$ 来说,每一个位置上的元素都有选取和未选取两种状态。我们可以用数字 1ドル$ 来表示选取该元素,用数字 0ドル$ 来表示不选取该元素。 +这样,任意一个 $n$ 位二进制数都唯一对应 $S$ 的一个子集。二进制的每一位对应集合中某个元素,1ドル$ 代表选取,0ドル$ 代表不选。 -那么我们就可以用一个长度为 $n$ 的二进制数来表示集合 $S$ 或者表示 $S$ 的子集。其中二进制的每一个二进位都对应了集合中某一个元素的选取状态。对于集合中第 $i$ 个元素来说,二进制对应位置上的 1ドル$ 代表该元素被选取,0ドル$ 代表该元素未被选取。 +举例说明,设 $S = \lbrace 5, 4, 3, 2, 1 \rbrace,ドル用 5ドル$ 位二进制数表示: -举个例子,比如长度为 5ドル$ 的集合 $S = \lbrace 5, 4, 3, 2, 1 \rbrace,ドル我们可以用一个长度为 5ドル$ 的二进制数来表示该集合。 +- 11111ドル_{(2)}$ 表示选取所有元素,即 $S$ 本身: -比如二进制数 11111ドル_{(2)}$ 就表示选取集合的第 1ドル$ 位、第 2ドル$ 位、第 3ドル$ 位、第 4ドル$ 位、第 5ドル$ 位元素,也就是集合 $\lbrace 5, 4, 3, 2, 1 \rbrace,ドル即集合 $S$ 本身。如下表所示: +| 元素位置 | 5 | 4 | 3 | 2 | 1 | +| :--------------: | :-: | :-: | :-: | :-: | :-: | +| 二进制位 | 1 | 1 | 1 | 1 | 1 | +| 选取状态 | 选取 | 选取 | 选取 | 选取 | 选取 | -| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 | -| :---------------- | :--: | :--: | :--: | :--: | :--: | -| 二进位对应值 | 1 | 1 | 1 | 1 | 1 | -| 对应选取状态 | 选取 | 选取 | 选取 | 选取 | 选取 | +- 10101ドル_{(2)}$ 表示选取第 1ドル$、3ドル$、5ドル$ 位元素,即 $\lbrace 5, 3, 1 \rbrace$: -再比如二进制数 10101ドル_{(2)}$ 就表示选取集合的第 1ドル$ 位、第 3ドル$ 位、第 5ドル$ 位元素,也就是集合 $\lbrace 5, 3, 1 \rbrace$。如下表所示: +| 元素位置 | 5 | 4 | 3 | 2 | 1 | +| :--------------: | :-: | :-: | :-: | :-: | :-: | +| 二进制位 | 1 | 0 | 1 | 0 | 1 | +| 选取状态 | 选取 | 未选取 | 选取 | 未选取 | 选取 | -| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 | -| :---------------- | :--: | :----: | :--: | :----: | :--: | -| 二进位对应值 | 1 | 0 | 1 | 0 | 1 | -| 对应选取状态 | 选取 | 未选取 | 选取 | 未选取 | 选取 | +- 01001ドル_{(2)}$ 表示选取第 1ドル$、4ドル$ 位元素,即 $\lbrace 4, 1 \rbrace$: -再比如二进制数 01001ドル_{(2)}$ 就表示选取集合的第 1ドル$ 位、第 4ドル$ 位元素,也就是集合 $\lbrace 4, 1 \rbrace$。如下标所示: +| 元素位置 | 5 | 4 | 3 | 2 | 1 | +| :--------------: | :-: | :-: | :-: | :-: | :-: | +| 二进制位 | 0 | 1 | 0 | 0 | 1 | +| 选取状态 | 未选取 | 选取 | 未选取 | 未选取 | 选取 | -| 集合 S 中元素位置 | 5 | 4 | 3 | 2 | 1 | -| :---------------- | :----: | :--: | :----: | :----: | :--: | -| 二进位对应值 | 0 | 1 | 0 | 0 | 1 | -| 对应选取状态 | 未选取 | 选取 | 未选取 | 未选取 | 选取 | +综上所述,对于长度为 $n$ 的集合 $S,ドル只需枚举 0ドル \sim 2^n - 1$(共 2ドル^n$ 种 $n$ 位二进制数),即可高效遍历并生成 $S$ 的所有子集。 -通过上面的例子我们可以得到启发:对于长度为 5ドル$ 的集合 $S$ 来说,我们只需要从 00000ドル \sim 11111$ 枚举一次(对应十进制为 0ドル \sim 2^5 - 1$)即可得到长度为 5ドル$ 的集合 $S$ 的所有子集。 - -我们将上面的例子拓展到长度为 $n$ 的集合 $S$。可以总结为: - -- 对于长度为 $n$ 的集合 $S$ 来说,只需要枚举 0ドル \sim 2^n - 1$(共 2ドル^n$ 种情况),即可得到集合 $S$ 的所有子集。 - -#### 3.3.2 二进制枚举子集代码 +#### 3.3.2 二进制枚举子集的实现代码 ```python class Solution: - def subsets(self, S): # 返回集合 S 的所有子集 - n = len(S) # n 为集合 S 的元素个数 - sub_sets = [] # sub_sets 用于保存所有子集 - for i in range(1 << n): # 枚举 0 ~ 2^n - 1 - sub_set = [] # sub_set 用于保存当前子集 - for j in range(n): # 枚举第 i 位元素 - if i>> j & 1: # 如果第 i 为元素对应二进位删改为 1,则表示选取该元素 - sub_set.append(S[j]) # 将选取的元素加入到子集 sub_set 中 - sub_sets.append(sub_set) # 将子集 sub_set 加入到所有子集数组 sub_sets 中 - return sub_sets # 返回所有子集 + def subsets(self, S): # 返回集合 S 的所有子集 + n = len(S) # n 为集合 S 的元素个数 + sub_sets = [] # sub_sets 用于保存所有子集 + for i in range(1 << n): # 枚举 0 ~ 2^n - 1 的所有可能,每个 i 表示一种选取方案 + sub_set = [] # sub_set 用于保存当前子集 + for j in range(n): # 枚举集合 S 的每一个元素 + # (i>> j) & 1 判断第 j 位是否为 1 + # 如果为 1,说明在当前子集方案 i 中选取了 S[j] + if (i>> j) & 1: # 如果第 j 位为 1,则选取 S[j] + sub_set.append(S[j]) # 将选取的元素 S[j] 加入到当前子集 sub_set 中 + sub_sets.append(sub_set) # 将当前子集 sub_set 加入到所有子集数组 sub_sets 中 + return sub_sets # 返回所有子集 ``` +## 4. 总结 + +位运算是一种直接操作二进制位的高效技巧,能够在底层实现中大幅提升算法的时间和空间效率,广泛应用于状态压缩、集合枚举、掩码处理等场景。 + +位运算基础操作包括按位与、或、异或、取反、左移和右移等,这些操作能够直接高效地处理二进制数据,常用于状态压缩、集合枚举和性能优化等场景。 + +在实际应用中,常通过二进制状态来表示集合的选取情况,从而高效枚举所有子集。其核心思想是:用 $n$ 位二进制数的每一位对应集合中的一个元素,1ドル$ 表示选中该元素,0ドル$ 表示未选中。只需遍历 0ドル$ 到 2ドル^n-1$ 的所有二进制数,即可快速生成集合的全部子集。 + + ## 练习题目 - [0190. 颠倒二进制位](https://github.com/ITCharge/AlgoNote/tree/main/docs/solutions/0100-0199/reverse-bits.md)

AltStyle によって変換されたページ (->オリジナル) /