|
4 | 4 | |
5 | 5 | 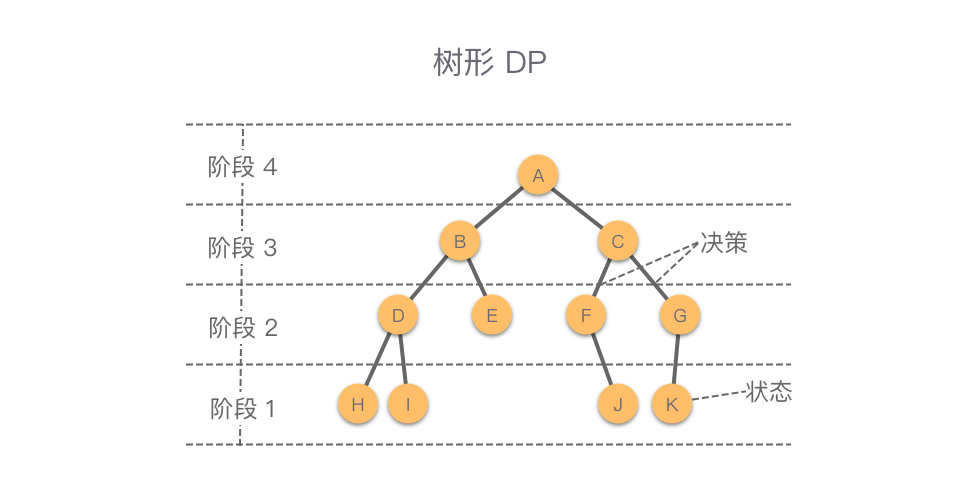 |
6 | 6 |
|
7 | | -> **树形 DP 的关键思路**:先通过递归的方式求解每棵子树,然后在回溯时,自底向上地从子节点向上进行状态转移。只有在当前节点的所有子树求解完毕之后,才可以求解当前节点,以及继续向上进行求解。 |
| 7 | +在使用树形 DP 时,常用的方向有以下两种: |
8 | 8 |
|
9 | | -## 2. 树形 DP 的简单例子 |
| 9 | +1. **自底向上**:通过递归的方式求解每棵子树,然后在回溯时,自底向上地从子节点向上进行状态转移。只有在当前节点的所有子树求解完毕之后,才可以求解当前节点,以及继续向上进行求解。 |
| 10 | +2. **自顶向下**:从根节点开始向下递归,逐层计算子节点的状态。这种方法常常使用记忆化搜索来避免重复计算,提高效率。 |
10 | 11 |
|
11 | | -### 2.1 二叉树的直径 |
| 12 | +自顶向下的树形 DP 问题比较少见,大部分树形 DP 都是采用「自底向上」的方向进行推导。 |
12 | 13 |
|
13 | | -#### 2.1.1 题目链接 |
| 14 | +## 2. 树形 DP 的简单例题 |
14 | 15 |
|
15 | | --[543. 二叉树的直径 - 力扣](https://leetcode.cn/problems/diameter-of-binary-tree/) |
| 16 | +下面以这道题为例,介绍一下树形 DP 的一般解题思路。 |
16 | 17 |
|
17 | | -#### 2.1.2 题目大意 |
| 18 | +##3. 换根树形 DP |
18 | 19 |
|
19 | | -**描述**:给定一个二叉树的根节点 $root$。 |
20 | | - |
21 | | -**要求**:计算该二叉树的直径长度。 |
22 | | - |
23 | | -**说明**: |
24 | | - |
25 | | -- **二叉树的直径长度**:二叉树中任意两个节点路径长度中的最大值。 |
26 | | -- 两节点之间的路径长度是以它们之间边的数目表示。 |
27 | | -- 这条路径可能穿过也可能不穿过根节点。 |
28 | | - |
29 | | -**示例**: |
30 | | - |
31 | | -- 示例 1: |
32 | | - |
33 | | -```Python |
34 | | -给定二叉树: |
35 | | - 1 |
36 | | - / \ |
37 | | - 2 3 |
38 | | - / \ |
39 | | - 4 5 |
40 | | -输出:3 |
41 | | -解释:该二叉树的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。 |
42 | | -``` |
43 | | - |
44 | | -#### 2.1.3 解题思路 |
45 | | - |
46 | | - |
47 | | - |
48 | | -## 3. 树形 DP 的应用 |
| 20 | +## 4. 树形 DP 的应用 |
0 commit comments