Skip to content

Navigation Menu

Sign in
Appearance settings

Search code, repositories, users, issues, pull requests...

Provide feedback

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly
Sign up
Appearance settings

Commit 8e202fb

Browse files
committed
更新题解列表
1 parent ec60676 commit 8e202fb

10 files changed

+257
-41
lines changed

‎Contents/00.Introduction/04.Solutions-List.md‎

Lines changed: 3 additions & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -1,4 +1,4 @@
1-
# LeetCode 题解(已完成 749 道)
1+
# LeetCode 题解(已完成 751 道)
22

33
| 题号 | 标题 | 题解 | 标签 | 难度 |
44
| :------ | :------ | :------ | :------ | :------ |
@@ -395,6 +395,7 @@
395395
| 0758 | [字符串中的加粗单词](https://leetcode.cn/problems/bold-words-in-string/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0758.%20%E5%AD%97%E7%AC%A6%E4%B8%B2%E4%B8%AD%E7%9A%84%E5%8A%A0%E7%B2%97%E5%8D%95%E8%AF%8D.md) | 字典树、数组、哈希表、字符串、字符串匹配 | 中等 |
396396
| 0763 | [划分字母区间](https://leetcode.cn/problems/partition-labels/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0763.%20%E5%88%92%E5%88%86%E5%AD%97%E6%AF%8D%E5%8C%BA%E9%97%B4.md) | 贪心、哈希表、双指针、字符串 | 中等 |
397397
| 0765 | [情侣牵手](https://leetcode.cn/problems/couples-holding-hands/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0765.%20%E6%83%85%E4%BE%A3%E7%89%B5%E6%89%8B.md) | 贪心、深度优先搜索、广度优先搜索、并查集、图 | 困难 |
398+
| 0766 | [托普利茨矩阵](https://leetcode.cn/problems/toeplitz-matrix/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0766.%20%E6%89%98%E6%99%AE%E5%88%A9%E8%8C%A8%E7%9F%A9%E9%98%B5.md) | 数组、矩阵 | 简单 |
398399
| 0771 | [宝石与石头](https://leetcode.cn/problems/jewels-and-stones/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0771.%20%E5%AE%9D%E7%9F%B3%E4%B8%8E%E7%9F%B3%E5%A4%B4.md) | 哈希表、字符串 | 简单 |
399400
| 0778 | [水位上升的泳池中游泳](https://leetcode.cn/problems/swim-in-rising-water/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0778.%20%E6%B0%B4%E4%BD%8D%E4%B8%8A%E5%8D%87%E7%9A%84%E6%B3%B3%E6%B1%A0%E4%B8%AD%E6%B8%B8%E6%B3%B3.md) | 深度优先搜索、广度优先搜索、并查集、数组、二分查找、矩阵、堆(优先队列) | 困难 |
400401
| 0779 | [第K个语法符号](https://leetcode.cn/problems/k-th-symbol-in-grammar/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/0779.%20%E7%AC%ACK%E4%B8%AA%E8%AF%AD%E6%B3%95%E7%AC%A6%E5%8F%B7.md) | 递归 | 中等 |
@@ -511,6 +512,7 @@
511512
| 1358 | [包含所有三种字符的子字符串数目](https://leetcode.cn/problems/number-of-substrings-containing-all-three-characters/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1358.%20%E5%8C%85%E5%90%AB%E6%89%80%E6%9C%89%E4%B8%89%E7%A7%8D%E5%AD%97%E7%AC%A6%E7%9A%84%E5%AD%90%E5%AD%97%E7%AC%A6%E4%B8%B2%E6%95%B0%E7%9B%AE.md) | 哈希表、字符串、滑动数组 | 中等 |
512513
| 1400 | [构造 K 个回文字符串](https://leetcode.cn/problems/construct-k-palindrome-strings/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1400.%20%E6%9E%84%E9%80%A0%20K%20%E4%B8%AA%E5%9B%9E%E6%96%87%E5%AD%97%E7%AC%A6%E4%B8%B2.md) | 贪心、哈希表、字符串、计数 | 中等 |
513514
| 1408 | [数组中的字符串匹配](https://leetcode.cn/problems/string-matching-in-an-array/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1408.%20%E6%95%B0%E7%BB%84%E4%B8%AD%E7%9A%84%E5%AD%97%E7%AC%A6%E4%B8%B2%E5%8C%B9%E9%85%8D.md) | 字符串、字符串匹配 | 简单 |
515+
| 1422 | [分割字符串的最大得分](https://leetcode.cn/problems/maximum-score-after-splitting-a-string/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1422.%20%E5%88%86%E5%89%B2%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E6%9C%80%E5%A4%A7%E5%BE%97%E5%88%86.md) | 字符串 | 简单 |
514516
| 1423 | [可获得的最大点数](https://leetcode.cn/problems/maximum-points-you-can-obtain-from-cards/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1423.%20%E5%8F%AF%E8%8E%B7%E5%BE%97%E7%9A%84%E6%9C%80%E5%A4%A7%E7%82%B9%E6%95%B0.md) | 数组、前缀和、滑动窗口 | 中等 |
515517
| 1438 | [绝对差不超过限制的最长连续子数组](https://leetcode.cn/problems/longest-continuous-subarray-with-absolute-diff-less-than-or-equal-to-limit/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1438.%20%E7%BB%9D%E5%AF%B9%E5%B7%AE%E4%B8%8D%E8%B6%85%E8%BF%87%E9%99%90%E5%88%B6%E7%9A%84%E6%9C%80%E9%95%BF%E8%BF%9E%E7%BB%AD%E5%AD%90%E6%95%B0%E7%BB%84.md) | 队列、数组、有序集合、滑动窗口、单调队列、堆(优先队列) | 中等 |
516518
| 1446 | [连续字符](https://leetcode.cn/problems/consecutive-characters/) | [Python](https://github.com/itcharge/LeetCode-Py/blob/main/Solutions/1446.%20%E8%BF%9E%E7%BB%AD%E5%AD%97%E7%AC%A6.md) | 字符串 | 简单 |

‎README.md‎

Lines changed: 1 addition & 1 deletion
Original file line numberDiff line numberDiff line change
@@ -259,4 +259,4 @@
259259
- [动态规划优化题目](./Contents/10.Dynamic-Programming/11.DP-Optimization/04.DP-Optimization-List.md)
260260

261261
## 11. 附加内容
262-
## [12. LeetCode 题解(已完成 749 道)](./Contents/00.Introduction/04.Solutions-List.md)
262+
## [12. LeetCode 题解(已完成 751 道)](./Contents/00.Introduction/04.Solutions-List.md)
Lines changed: 69 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,69 @@
1+
# [0766. 托普利茨矩阵](https://leetcode.cn/problems/toeplitz-matrix/)
2+
3+
- 标签:数组、矩阵
4+
- 难度:简单
5+
6+
## 题目大意
7+
8+
**描述**:给定一个 $m \times n$ 大小的矩阵 $matrix$。
9+
10+
**要求**:如果 $matrix$ 是托普利茨矩阵,则返回 `True`;否则返回 `False`。
11+
12+
**说明**:
13+
14+
- **托普利茨矩阵**:矩阵上每一条由左上到右下的对角线上的元素都相同。
15+
- $m == matrix.length$。
16+
- $n == matrix[i].length$。
17+
- 1ドル \le m, n \le 20$。
18+
- 0ドル \le matrix[i][j] \le 99$。
19+
20+
**示例**:
21+
22+
- 示例 1:
23+
24+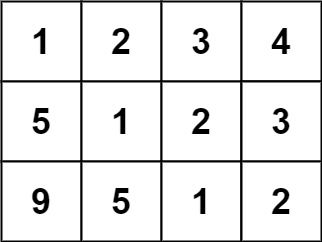
![](https://assets.leetcode.com/uploads/2020/11/04/ex1.jpg)
25+
26+
```Python
27+
输入:matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
28+
输出:true
29+
解释:
30+
在上述矩阵中, 其对角线为:
31+
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。
32+
各条对角线上的所有元素均相同, 因此答案是 True。
33+
```
34+
35+
- 示例 2:
36+
37+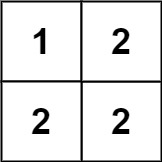
![](https://assets.leetcode.com/uploads/2020/11/04/ex2.jpg)
38+
39+
```Python
40+
输入:matrix = [[1,2],[2,2]]
41+
输出:false
42+
解释:
43+
对角线 "[1, 2]" 上的元素不同。
44+
```
45+
46+
## 解题思路
47+
48+
### 思路 1:简单模拟
49+
50+
1. 两层循环遍历矩阵,依次判断矩阵当前位置 $(i, j)$ 上的值 $matrix[i][j]$ 与其左上角位置 $(i - 1, j - 1)$ 位置上的值 $matrix[i - 1][j - 1]$ 是否相等。
51+
2. 如果不相等,则返回 `False`。
52+
3. 遍历完,则返回 `True`。
53+
54+
### 思路 1:代码
55+
56+
```Python
57+
class Solution:
58+
def isToeplitzMatrix(self, matrix: List[List[int]]) -> bool:
59+
for i in range(1, len(matrix)):
60+
for j in range(1, len(matrix[0])):
61+
if matrix[i][j] != matrix[i - 1][j - 1]:
62+
return False
63+
return True
64+
```
65+
66+
### 思路 1:复杂度分析
67+
68+
- **时间复杂度**:$O(m \times n),ドル其中 $m$、$n$ 分别是矩阵 $matrix$ 的行数、列数。
69+
- **空间复杂度**:$O(m \times n)$。

‎Solutions/1009. 十进制整数的反码.md‎

Lines changed: 6 additions & 6 deletions
Original file line numberDiff line numberDiff line change
@@ -5,7 +5,7 @@
55

66
## 题目大意
77

8-
**描述**:给定一个十进制数 `n`。
8+
**描述**:给定一个十进制数 $n$。
99

1010
**要求**:返回其二进制表示的反码对应的十进制整数。
1111

@@ -35,11 +35,11 @@
3535

3636
### 思路 1:模拟
3737

38-
1. 将十进制数 `n` 转为二进制 `binary`。
39-
2. 遍历二进制 `binary` 的每一个数位 `digit`。
40-
1. 如果 `digit` 为 `0`,则将其转为 `1`,存入答案 `res` 中。
41-
2. 如果 `digit` 为 `1`,则将其转为 `0`,存入答案 `res` 中。
42-
3. 返回答案 `res`。
38+
1. 将十进制数 $n$ 转为二进制 $binary$。
39+
2. 遍历二进制 $binary$ 的每一个数位 $digit$。
40+
1. 如果 $digit$ 为 0ドル$,则将其转为 1ドル$,存入答案 $res$ 中。
41+
2. 如果 $digit$ 为 1ドル$,则将其转为 0ドル$,存入答案 $res$ 中。
42+
3. 返回答案 $res$。
4343

4444
### 思路 1:代码
4545

‎Solutions/1037. 有效的回旋镖.md‎

Lines changed: 21 additions & 21 deletions
Original file line numberDiff line numberDiff line change
@@ -5,14 +5,14 @@
55

66
## 题目大意
77

8-
**描述**:给定一个数组 `points`,其中 `points[i] = [xi, yi]` 表示平面上的一个点。
8+
**描述**:给定一个数组 $points$,其中 $points[i] = [xi, yi]$ 表示平面上的一个点。
99

1010
**要求**:如果这些点构成一个回旋镖,则返回 `True`,否则,则返回 `False`。
1111

1212
**说明**:
1313

1414
- **回旋镖**:定义为一组三个点,这些点各不相同且不在一条直线上。
15-
- `points.length == 3`
15+
- $points.length == 3$。
1616
- $points[i].length == 2$。
1717
- 0ドル \le xi, yi \le 100$。
1818

@@ -21,41 +21,41 @@
2121
- 示例 1:
2222

2323
```Python
24+
输入:points = [[1,1],[2,3],[3,2]]
25+
输出:True
2426
```
2527

2628
- 示例 2:
2729

2830
```Python
31+
输入:points = [[1,1],[2,2],[3,3]]
32+
输出:False
2933
```
3034

3135
## 解题思路
3236

3337
### 思路 1:
3438

35-
当三个点满足: (x2−x1)×ばつ(y3−y1)=(x3−x1)×ばつ(y2−y1)(x_2 - x_1) \times (y_3 - y_1) = (x_3 - x_1) \times (y_2 - y_1)(*x*2−*x*1)×ばつ(*y*3−*y*1)=(*x*3−*x*1)×ばつ(*y*2−*y*1) 时共线,否则为回旋镖。
39+
设三点坐标为 $A = (x1, y1),ドル$B = (x2, y2),ドル$C = (x3, y3),ドル则向量 $\overrightarrow{AB} = (x2 - x1, y2 - y1),ドル$\overrightarrow{BC} = (x3 - x2, y3 - y2)$。
3640

37-
### 思路 1:代码
38-
39-
```Python
40-
41-
```
42-
43-
### 思路 1:复杂度分析
41+
如果三点共线,则应满足:$\overrightarrow{AB} \times \overrightarrow{BC} = (x2 − x1) \times (y3 − y2) - (x3 − x2) \times (y2 − y1) = 0$。
4442

45-
- **时间复杂度**:
46-
- **空间复杂度**:
43+
如果三点不共线,则应满足:$\overrightarrow{AB} \times \overrightarrow{BC} = (x2 − x1) \times (y3 − y2) - (x3 − x2) \times (y2 − y1) \ne 0$。
4744

48-
### 思路 2:
49-
50-
51-
52-
### 思路 2:代码
45+
### 思路 1:代码
5346

5447
```Python
55-
48+
class Solution:
49+
def isBoomerang(self, points: List[List[int]]) -> bool:
50+
x1, y1 = points[0]
51+
x2, y2 = points[1]
52+
x3, y3 = points[2]
53+
cross1 = (x2 - x1) * (y3 - y2)
54+
cross2 = (x3 - x2) * (y2 - y1)
55+
return cross1 - cross2 != 0
5656
```
5757

58-
### 思路 2:复杂度分析
58+
### 思路 1:复杂度分析
5959

60-
- **时间复杂度**:
61-
- **空间复杂度**:
60+
- **时间复杂度**:$O(1)$。
61+
- **空间复杂度**:$O(1)$。
Lines changed: 67 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,67 @@
1+
# 题目相关
2+
3+
- 标签:数组
4+
- 难度:简单
5+
6+
## 题目大意
7+
8+
**描述**:环形公交路线上有 $n$ 个站,序号为 0ドル \sim n - 1$。给定一个数组 $distance$ 表示每一对相邻公交站之间的距离,其中 $distance[i]$ 表示编号为 $i$ 的车站与编号为 $(i + 1) \mod n$ 的车站之间的距离。再给定乘客的出发点编号 $start$ 和目的地编号 $destination$。
9+
10+
**要求**:返回乘客从出发点 $start$ 到目的地 $destination$ 之间的最短距离。
11+
12+
**说明**:
13+
14+
- 1ドル \le n \le 10^4$。
15+
- $distance.length == n$。
16+
- 0ドル \le start, destination < n$。
17+
- 0ドル \le distance[i] \le 10^4$。
18+
19+
**示例**:
20+
21+
- 示例 1:
22+
23+
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/09/08/untitled-diagram-1.jpg)
24+
25+
```Python
26+
输入:distance = [1,2,3,4], start = 0, destination = 1
27+
输出:1
28+
解释:公交站 0 和 1 之间的距离是 1 或 9,最小值是 1。
29+
```
30+
31+
- 示例 2:
32+
33+
![](https://assets.leetcode-cn.com/aliyun-lc-upload/uploads/2019/09/08/untitled-diagram-1-1.jpg)
34+
35+
```Python
36+
输入:distance = [1,2,3,4], start = 0, destination = 2
37+
输出:3
38+
解释:公交站 0 和 2 之间的距离是 3 或 7,最小值是 3。
39+
```
40+
41+
## 解题思路
42+
43+
### 思路 1:简单模拟
44+
45+
1. 因为 $start$ 和 $destination$ 的先后顺序不影响结果,为了方便计算,我们先令 $start \le destination$。
46+
2. 遍历数组 $distance,ドル计算出 $[start, destination]$ 之间的距离和 $dist$。
47+
3. 计算出环形路线中 $[destination, start]$ 之间的距离和为 $sum(distance) - dist$。
48+
4. 比较 2ドル \sim 3$ 中两个距离的大小,将距离最小值作为答案返回。
49+
50+
### 思路 1:代码
51+
52+
```Python
53+
class Solution:
54+
def distanceBetweenBusStops(self, distance: List[int], start: int, destination: int) -> int:
55+
start, destination = min(start, destination), max(start, destination)
56+
dist = 0
57+
for i in range(len(distance)):
58+
if start <= i < destination:
59+
dist += distance[i]
60+
61+
return min(dist, sum(distance) - dist)
62+
```
63+
64+
### 思路 1:复杂度分析
65+
66+
- **时间复杂度**:$O(n)$。
67+
- **空间复杂度**:$O(1)$。
Lines changed: 75 additions & 0 deletions
Original file line numberDiff line numberDiff line change
@@ -0,0 +1,75 @@
1+
# [1422. 分割字符串的最大得分](https://leetcode.cn/problems/maximum-score-after-splitting-a-string/)
2+
3+
- 标签:字符串
4+
- 难度:简单
5+
6+
## 题目大意
7+
8+
**描述**:给定一个由若干 0ドル$ 和 1ドル$ 组成的字符串。将字符串分割成两个非空子字符串的得分为:左子字符串中 0ドル$ 的数量 + 右子字符串中 1ドル$ 的数量。
9+
10+
**要求**:计算并返回该字符串分割成两个非空子字符串(即左子字符串和右子字符串)所能获得的最大得分。
11+
12+
**说明**:
13+
14+
- 2ドル \le s.length \le 500$。
15+
- 字符串 $s$ 仅由字符 0ドル$ 和 1ドル$ 组成。
16+
17+
**示例**:
18+
19+
- 示例 1:
20+
21+
```Python
22+
输入:s = "011101"
23+
输出:5
24+
解释:
25+
将字符串 s 划分为两个非空子字符串的可行方案有:
26+
左子字符串 = "0" 且 右子字符串 = "11101",得分 = 1 + 4 = 5
27+
左子字符串 = "01" 且 右子字符串 = "1101",得分 = 1 + 3 = 4
28+
左子字符串 = "011" 且 右子字符串 = "101",得分 = 1 + 2 = 3
29+
左子字符串 = "0111" 且 右子字符串 = "01",得分 = 1 + 1 = 2
30+
左子字符串 = "01110" 且 右子字符串 = "1",得分 = 2 + 1 = 3
31+
```
32+
33+
- 示例 2:
34+
35+
```Python
36+
输入:s = "00111"
37+
输出:5
38+
解释:当 左子字符串 = "00" 且 右子字符串 = "111" 时,我们得到最大得分 = 2 + 3 = 5
39+
```
40+
41+
## 解题思路
42+
43+
### 思路 1:前缀和
44+
45+
1. 遍历字符串 $s,ドル使用前缀和数组来记录每个前缀子字符串中 1ドル$ 的个数。
46+
2. 再次遍历字符串 $s,ドル枚举每个分割点,利用前缀和数组计算出当前分割出的左子字符串中 1ドル$ 的个数与右子字符串中 0ドル$ 的个数,并计算当前得分,然后更新最大得分。
47+
3. 返回最大得分作为答案。
48+
49+
### 思路 1:代码
50+
51+
```Python
52+
class Solution:
53+
def maxScore(self, s: str) -> int:
54+
size = len(s)
55+
one_cnts = [0 for _ in range(size + 1)]
56+
57+
for i in range(1, size + 1):
58+
if s[i - 1] == '1':
59+
one_cnts[i] = one_cnts[i - 1] + 1
60+
else:
61+
one_cnts[i] = one_cnts[i - 1]
62+
63+
ans = 0
64+
for i in range(1, size):
65+
left_score = i - one_cnts[i]
66+
right_score = one_cnts[size] - one_cnts[i]
67+
ans = max(ans, left_score + right_score)
68+
69+
return ans
70+
```
71+
72+
### 思路 1:复杂度分析
73+
74+
- **时间复杂度**:$O(n),ドル其中 $n$ 为字符串 $s$ 的长度。
75+
- **空间复杂度**:$O(n)$。

‎Solutions/1876. 长度为三且各字符不同的子字符串.md‎

Lines changed: 4 additions & 4 deletions
Original file line numberDiff line numberDiff line change
@@ -5,16 +5,16 @@
55

66
## 题目大意
77

8-
**描述**:给定搞一个字符串 `s`。
8+
**描述**:给定搞一个字符串 $s$。
99

10-
**要求**:返回 `s` 中长度为 3ドル$ 的好子字符串的数量。如果相同的好子字符串出现多次,则每一次都应该被记入答案之中。
10+
**要求**:返回 $s$ 中长度为 3ドル$ 的好子字符串的数量。如果相同的好子字符串出现多次,则每一次都应该被记入答案之中。
1111

1212
**说明**:
1313

1414
- **子字符串**:指的是一个字符串中连续的字符序列。
1515
- **好子字符串**:如果一个字符串中不含有任何重复字符,则称这个字符串为好子字符串。
1616
- 1ドル \le s.length \le 100$。
17-
- `s` 只包含小写英文字母。
17+
- $s$ 只包含小写英文字母。
1818

1919
**示例**:
2020

@@ -40,7 +40,7 @@
4040

4141
### 思路 1:模拟
4242

43-
1. 遍历长度为 3 的子字符串。
43+
1. 遍历字符串 $s$ 中长度为 3 的子字符串。
4444
2. 判断子字符串中的字符是否有重复。如果没有重复,则答案进行计数。
4545
3. 遍历完输出答案。
4646

0 commit comments

Comments
(0)

AltStyle によって変換されたページ (->オリジナル) /