|
26 | 26 |
|
27 | 27 | 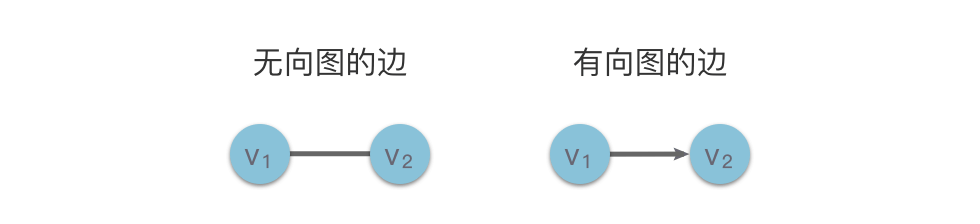 |
28 | 28 |
|
29 | | -如果无向图中有 $n$ 个顶点,则无向图中最多有 $n * (n - 1) / 2$ 条边。而具有 $n * (n - 1) / 2$ 条边的无向图称为 **「完全无向图(Completed Undirected Graph)」**。 |
| 29 | +如果无向图中有 $n$ 个顶点,则无向图中最多有 $n \times (n - 1) / 2$ 条边。而具有 $n \times (n - 1) / 2$ 条边的无向图称为 **「完全无向图(Completed Undirected Graph)」**。 |
30 | 30 |
|
31 | | -如果有向图中有 $n$ 个顶点,则有向图中最多有 $n * (n - 1)$ 条弧。而具有 $n * (n - 1)$ 条弧的有向图称为 **「完全有向图(Completed Directed Graph)」**。 |
| 31 | +如果有向图中有 $n$ 个顶点,则有向图中最多有 $n \times (n - 1)$ 条弧。而具有 $n \times (n - 1)$ 条弧的有向图称为 **「完全有向图(Completed Directed Graph)」**。 |
32 | 32 |
|
33 | | -如下图所示,左侧为包含 `4` 个顶点的完全无向图,右侧为包含 `4` 个顶点的完全有向图。 |
| 33 | +如下图所示,左侧为包含 4ドル$ 个顶点的完全无向图,右侧为包含 4ドル$ 个顶点的完全有向图。 |
34 | 34 |
|
35 | 35 | 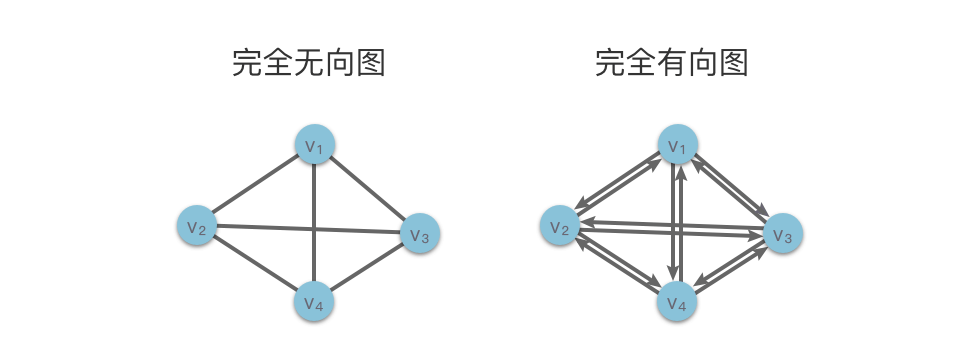 |
36 | 36 |
|
37 | 37 | 下面介绍一下无向图和有向图中一个重要概念 **「顶点的度」**。 |
38 | 38 |
|
39 | 39 | - **顶点的度**:与该顶点 $v_i$ 相关联的边的条数,记为 $TD(v_i)$。 |
40 | 40 |
|
41 | | -例如上图左侧的完全无向图中,顶点 $v_3$ 的度为 `3`。 |
| 41 | +例如上图左侧的完全无向图中,顶点 $v_3$ 的度为 3ドル$。 |
42 | 42 |
|
43 | 43 | 而对于有向图,我们可以将顶点的度分为 **「顶点的出度」** 和 **「顶点的入度」**。 |
44 | 44 |
|
45 | 45 | - **顶点的出度**:以该顶点 $v_i$ 为出发点的边的条数,记为 $OD(v_i)$。 |
46 | 46 | - **顶点的入度**:以该顶点 $v_i$ 为终止点的边的条数,记为 $ID(v_i)$。 |
47 | 47 | - 有向图中某顶点的度 = 该顶点的出度 + 该顶点的入度,即 $TD(v_i) = OD(v_i) + ID(v_i)$。 |
48 | 48 |
|
49 | | -例如上图右侧的完全有向图中,顶点 $v_3$ 的出度为 `3`,入度为 `3`,顶点 $v_3$ 的度为 `3 + 3 = 6`。 |
| 49 | +例如上图右侧的完全有向图中,顶点 $v_3$ 的出度为 3ドル$,入度为 3ドル$,顶点 $v_3$ 的度为 $3 + 3 = 6$。 |
50 | 50 |
|
51 | 51 | ### 2.2 环形图和无环图 |
52 | 52 |
|
53 | 53 | **「路径」** 是图中的一个重要概念,对于图 $G = (V, E),ドル如果存在顶点序列 $v_{i_0}, v_{i_1}, v_{i_2},... , v_{i_m},ドル使得 $(v_{i_0}, v_{i_1}),(v_{i_1}, v_{i_2}),...,(v_{i_{m-1}}, v_{i_m}) \in E$(即他们都是图 G 的边,对于有向图则是 $\langle v_{i_0}, v_{i_1} \rangle,\langle v_{i_1}, v_{i_2} \rangle,...,\langle v_{i_{m-1}}, v_{i_m} \rangle \in E$),则称该顶点序列为顶点 $v_{i_0}$ 和顶点 $v_{i_m}$ 之间的一条路径,其中 $v_{i_0}$ 是这条路径的起始点,$v_{i_m}$ 是这条路径的终止点。 |
54 | 54 |
|
55 | 55 | 简单来说,如果顶点 $v_{i_0}$ 可以通过一系列的顶点和边,到达顶点 $v_{i_m},ドル则称顶点 $v_{i_0}$ 和顶点 $v_{i_m}$ 之间有一条路径,其中经过的顶点序列则称为两个顶点之间的路径。 |
56 | 56 |
|
57 | | -- **环(Circle)**:如果一条路径的起始点和终止点相同(即 $v_{i_0} = v_{i_m}$ ),则称这条路径为「回路」或者「环」。 |
| 57 | +- **环(Circle)**:如果一条路径的起始点和终止点相同(即 $v_{i_0} == v_{i_m}$ ),则称这条路径为「回路」或者「环」。 |
58 | 58 |
|
59 | 59 | - **简单路径**:顶点序列中顶点不重复出现的路径称为「简单路径」。 |
60 | 60 |
|
|
124 | 124 |
|
125 | 125 | 根据图中边的稀疏程度,我们可以将图分为「稠密图」和「稀疏图」。这是一个模糊的概念,目前为止还没有给出一个量化的定义。 |
126 | 126 |
|
127 | | -- **稠密图(Dense Graph)**:有很多条边或弧(边的条数 e 接近于完全图的边数)的图称为稠密图。 |
128 | | -- **稀疏图(Sparse Graph)**:有很少条边或弧(边的条数 e 远小于完全图的边数,如 $e < nlog_2n$)的图称为稀疏图。 |
| 127 | +- **稠密图(Dense Graph)**:有很多条边或弧(边的条数 $e$ 接近于完全图的边数)的图称为稠密图。 |
| 128 | +- **稀疏图(Sparse Graph)**:有很少条边或弧(边的条数 $e$ 远小于完全图的边数,如 $e < n \times \log_2n$)的图称为稀疏图。 |
129 | 129 |
|
130 | 130 | ## 参考资料 |
131 | 131 |
|
|
0 commit comments