|
| 1 | +# [0892. 三维形体的表面积](https://leetcode.cn/problems/surface-area-of-3d-shapes/) |
| 2 | + |
| 3 | +- 标签:几何、数组、数学、矩阵 |
| 4 | +- 难度:简单 |
| 5 | + |
| 6 | +## 题目链接 |
| 7 | + |
| 8 | +- [0892. 三维形体的表面积 - 力扣](https://leetcode.cn/problems/surface-area-of-3d-shapes/) |
| 9 | + |
| 10 | +## 题目大意 |
| 11 | + |
| 12 | +**描述**:给定一个 $n \times n$ 的网格 $grid,ドル上面放置着一些 1ドル \times 1 \times 1$ 的正方体。每个值 $v = grid[i][j]$ 表示 $v$ 个正方体叠放在对应单元格 $(i, j)$ 上。 |
| 13 | + |
| 14 | +放置好正方体后,任何直接相邻的正方体都会互相粘在一起,形成一些不规则的三维形体。 |
| 15 | + |
| 16 | +**要求**:返回最终这些形体的总面积。 |
| 17 | + |
| 18 | +**说明**: |
| 19 | + |
| 20 | +- 每个形体的底面也需要计入表面积中。 |
| 21 | + |
| 22 | +**示例**: |
| 23 | + |
| 24 | +- 示例 1: |
| 25 | + |
| 26 | + |
| 27 | + |
| 28 | +```python |
| 29 | +输入:grid = [[1,2],[3,4]] |
| 30 | +输出:34 |
| 31 | +``` |
| 32 | + |
| 33 | +- 示例 2: |
| 34 | + |
| 35 | +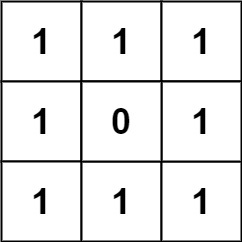 |
| 36 | + |
| 37 | +```python |
| 38 | +输入:grid = [[1,1,1],[1,0,1],[1,1,1]] |
| 39 | +输出:32 |
| 40 | +``` |
| 41 | + |
| 42 | +## 解题思路 |
| 43 | + |
| 44 | +### 思路 1:模拟 |
| 45 | + |
| 46 | +使用二重循环遍历所有的正方体,计算每一个正方体所贡献的表面积,将其累积起来即为答案。 |
| 47 | + |
| 48 | +而每一个正方体所贡献的表面积,可以通过枚举当前正方体前后左右相邻四个方向上的正方体的个数,从而通过判断计算得出。 |
| 49 | + |
| 50 | +- 如果当前位置 $(row, col)$ 存在正方体,则正方体在上下位置上起码贡献了 2ドル$ 的表面积。 |
| 51 | +- 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上不存在正方体,说明当前正方体在该方向为最外侧,则 $(row, col)$ 位置所贡献的表面积为当前位置上的正方体个数,即 $grid[row][col]$。 |
| 52 | +- 如果当前位置 $(row, col)$ 的相邻位置 $(new\underline{}row, new\underline{}col)$ 上存在正方体: |
| 53 | + - 如果 $grid[row][col] > grid[new\underline{}row][new\underline{}col],ドル说明 $grid[row][col]$ 在该方向上底面一部分被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了,则 $(row, col)$ 位置所贡献的表面积为 $grid[row][col] - grid[new_row][new_col]$。 |
| 54 | + - 如果 $grid[row][col] \le grid[new\underline{}row][new\underline{}col],ドル说明 $grid[row][col]$ 在该方向上完全被 $grid[new\underline{}row][new\underline{}col]$ 遮盖了,则 $(row, col)$ 位置所贡献的表面积为 0ドル$。 |
| 55 | + |
| 56 | +### 思路 1:代码 |
| 57 | + |
| 58 | +```Python |
| 59 | +class Solution: |
| 60 | + def surfaceArea(self, grid: List[List[int]]) -> int: |
| 61 | + directions = [(-1, 0), (0, 1), (1, 0), (0, -1)] |
| 62 | + size = len(grid) |
| 63 | + |
| 64 | + ans = 0 |
| 65 | + for row in range(size): |
| 66 | + for col in range(size): |
| 67 | + if grid[row][col]: |
| 68 | + # 底部、顶部贡献表面积 |
| 69 | + ans += 2 |
| 70 | + for direction in directions: |
| 71 | + new_row = row + direction[0] |
| 72 | + new_col = col + direction[1] |
| 73 | + if 0 <= new_row < size and 0 <= new_col < size: |
| 74 | + if grid[row][col] > grid[new_row][new_col]: |
| 75 | + add = grid[row][col] - grid[new_row][new_col] |
| 76 | + else: |
| 77 | + add = 0 |
| 78 | + else: |
| 79 | + add = grid[row][col] |
| 80 | + ans += add |
| 81 | + return ans |
| 82 | +``` |
| 83 | + |
| 84 | +### 思路 1:复杂度分析 |
| 85 | + |
| 86 | +- **时间复杂度**:$O(n^2),ドル其中 $n$ 为二位数组 $grid$ 的行数或列数。 |
| 87 | +- **空间复杂度**:$O(1)$。 |
| 88 | + |
0 commit comments