|
5 | 5 |
|
6 | 6 | ## 题目大意 |
7 | 7 |
|
8 | | -给定一个 `m * n` 的二维数组 `board`,每一个格子都可以看做是一个细胞。每个细胞都有一个初始状态:`1` 代表活细胞,`0` 代表死细胞。每个细胞与其相邻的八个位置(水平、垂直、对角线)细胞遵循以下生存规律: |
| 8 | +**描述**:给定一个 $m \times n$ 大小的二维数组 $board$,每一个格子都可以看做是一个细胞。每个细胞都有一个初始状态:1ドル$ 代表活细胞,0ドル$ 代表死细胞。每个细胞与其相邻的八个位置(水平、垂直、对角线)细胞遵循以下生存规律: |
9 | 9 |
|
10 | | -- 如果活细胞周围八个位置的活细胞数少于 2 个,则该位置活细胞死亡; |
11 | | -- 如果活细胞周围八个位置有 2 个或 3 个活细胞,则该位置活细胞仍然存活; |
12 | | -- 如果活细胞周围八个位置有超过 3 个活细胞,则该位置活细胞死亡; |
13 | | -- 如果死细胞周围正好有 3 个活细胞,则该位置死细胞复活。 |
| 10 | +- 如果活细胞周围八个位置的活细胞数少于 2ドル$ 个,则该位置活细胞死亡; |
| 11 | +- 如果活细胞周围八个位置有 2ドル$ 个或 3ドル$ 个活细胞,则该位置活细胞仍然存活; |
| 12 | +- 如果活细胞周围八个位置有超过 3ドル$ 个活细胞,则该位置活细胞死亡; |
| 13 | +- 如果死细胞周围正好有 3ドル$ 个活细胞,则该位置死细胞复活。 |
14 | 14 |
|
15 | 15 | 二维数组代表的下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的的。其中细胞的出生和死亡是同时发生的。 |
16 | 16 |
|
17 | | -现在给定 `m * n` 的二维数组 `board` 的当前状态。 |
| 17 | +现在给定 $m \times n$ 的二维数组 $board$ 的当前状态。 |
18 | 18 |
|
19 | | -要求:返回下一个状态。 |
| 19 | +**要求**:返回下一个状态。 |
| 20 | + |
| 21 | +**说明**: |
| 22 | + |
| 23 | +- $m == board.length$。 |
| 24 | +- $n == board[i].length$。 |
| 25 | +- 1ドル \le m, n \le 25$。 |
| 26 | +- $board[i][j]$ 为 0ドル$ 或 1ドル$。 |
| 27 | +- **进阶**: |
| 28 | + - 你可以使用原地算法解决本题吗?请注意,面板上所有格子需要同时被更新:你不能先更新某些格子,然后使用它们的更新后的值再更新其他格子。 |
| 29 | + - 本题中,我们使用二维数组来表示面板。原则上,面板是无限的,但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题? |
| 30 | + |
| 31 | + |
| 32 | +**示例**: |
| 33 | + |
| 34 | +- 示例 1: |
| 35 | + |
| 36 | +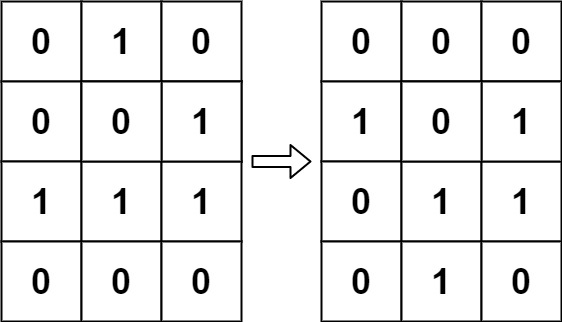 |
| 37 | + |
| 38 | +```Python |
| 39 | +输入:board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] |
| 40 | +输出:[[0,0,0],[1,0,1],[0,1,1],[0,1,0]] |
| 41 | +``` |
| 42 | + |
| 43 | +- 示例 2: |
| 44 | + |
| 45 | +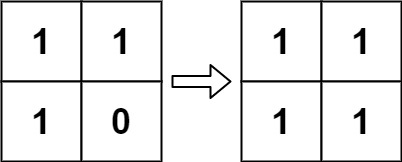 |
| 46 | + |
| 47 | +```Python |
| 48 | +输入:board = [[1,1],[1,0]] |
| 49 | +输出:[[1,1],[1,1]] |
| 50 | +``` |
20 | 51 |
|
21 | 52 | ## 解题思路 |
22 | 53 |
|
| 54 | +### 思路 1:模拟 |
| 55 | + |
23 | 56 | 因为下一个状态隐含了过去细胞的状态,所以不能直接在原二维数组上直接进行修改。细胞的状态总共有四种情况: |
24 | 57 |
|
25 | | -- 死细胞 -> 死细胞,即 `0` -> `0`。 |
26 | | -- 死细胞 -> 活细胞,即 `0` -> `1`。 |
27 | | -- 活细胞 -> 活细胞,即 `1` -> `1`。 |
28 | | -- 活细胞 -> 死细胞,即 `1` -> `0`。 |
| 58 | +- 死细胞 -> 死细胞,即 0ドル \rightarrow 0$。 |
| 59 | +- 死细胞 -> 活细胞,即 0ドル \rightarrow 1$。 |
| 60 | +- 活细胞 -> 活细胞,即 1ドル \rightarrow 1$。 |
| 61 | +- 活细胞 -> 死细胞,即 1ドル \rightarrow 0$。 |
29 | 62 |
|
30 | | -死细胞 -> 死细胞,活细胞 -> 活细胞,不会对前后状态造成影响,所以主要考虑另外两种情况。我们把活细胞 -> 死细胞暂时标记为 `-1`,并且统计每个细胞周围活细胞数量时,使用绝对值统计,这样 `abs(-1)` 也可以暂时标记为活细胞。然后把死细胞 -> 活细胞暂时标记为 `2`,这样判断的时候也不会统计上去。然后开始遍历。 |
| 63 | +死细胞 -> 死细胞,活细胞 -> 活细胞,不会对前后状态造成影响,所以主要考虑另外两种情况。我们把活细胞 -> 死细胞暂时标记为 $-1$,并且统计每个细胞周围活细胞数量时,使用绝对值统计,这样 $abs(-1)$ 也可以暂时标记为活细胞。然后把死细胞 -> 活细胞暂时标记为 2ドル$,这样判断的时候也不会统计上去。然后开始遍历。 |
31 | 64 |
|
32 | 65 | - 遍历二维数组的每一个位置。并对该位置遍历周围八个位置,计算出八个位置上的活细胞数量。 |
33 | | - - 如果此位置是活细胞,并且周围活细胞少于 `2` 个或超过 `3` 个,则将其暂时标记为 `-1`,意为此细胞死亡。 |
34 | | - - 如果此位置是死细胞,并且周围有 3 个活细胞,则将暂时标记为 `1`,意为此细胞复活。 |
35 | | -- 遍历完之后,再次遍历一遍二维数组,如果该位置为 `-1`,将其赋值为 `0`,如果该位置为 `2`,将其赋值为 `1`。 |
| 66 | + - 如果此位置是活细胞,并且周围活细胞少于 2ドル$ 个或超过 3ドル$ 个,则将其暂时标记为 $-1$,意为此细胞死亡。 |
| 67 | + - 如果此位置是死细胞,并且周围有 3ドル$ 个活细胞,则将暂时标记为 2ドル$,意为此细胞复活。 |
| 68 | +- 遍历完之后,再次遍历一遍二维数组,如果该位置为 $-1$,将其赋值为 0ドル$,如果该位置为 2ドル$,将其赋值为 1ドル$。 |
36 | 69 |
|
37 | | -##代码 |
| 70 | +### 思路 1:代码 |
38 | 71 |
|
39 | 72 | ```Python |
40 | 73 | class Solution: |
@@ -69,3 +102,8 @@ class Solution: |
69 | 102 | board[row][col] = 1 |
70 | 103 | ``` |
71 | 104 |
|
| 105 | +### 思路 1:复杂度分析 |
| 106 | + |
| 107 | +- **时间复杂度**:$O(m \times n),ドル其中 $m$、$n$ 分别为 $board$ 的行数和列数。 |
| 108 | +- **空间复杂度**:$O(m \times n)$。 |
| 109 | + |
0 commit comments